1. Статическая сторона задачи.

отсюда (а)

2. Геометрическая сторона задачи.

Под действием силы РбалкаАСопустится и наклонится, заняв положениеА₁С₁(рис.2.48,б).

Исходя из силовой схемы, определяем степень статической неопределимости: S=3-2=1. Следовательно, для определения трех неизвестных силN₁,N₂иN₃требуется одно дополнительное уравнение. Оно составляется из условия совместности деформации стержней по схеме деформированной системы:

(b)

или

3. Физическая сторона задачи.

По закону Гука имеем:

Подставляя это в (b), получаем:

(с)

4. Определение неизвестных.

Решая совместно уравнения (с)и(а), находим:

5. Энергетическая проверка.

Работа Авнешней силыРна перемещенииравна сумме потенциальной энергии деформации стержней системы U:А=U

(d)

где

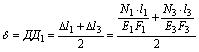
Подставляя все в (d), получим

33.811,2=33.811,2;

т. е. равенство (d)удовлетворяется.

 

Пример 22.

Определить усилия в стержнях, возникающие при сборке узла А из-за неточностиизготовления элементов системы (устранение технологического зазора) рис. 2.49, а.

Дано: E₁=E₂=E;F₁=2F₂=2F;l₁=l₂=l;

Рис. 2.49

 

Решение.

1. Статическая сторона задачи.

тогда и (а)

2. Геометрическая сторона задачи.

После принудительной сборки конструкции шарнир А займет положениеА₁(рис. 2.49,б). Стержни 1 и 2 окажутся растянутыми. В соответствии с этим схема деформированной системы имеет вид, показанный на рис. 2.49, б.

Степень статической неопределимости S=3-2=1. Исходя из схемы деформированного состояния, составляем условие совместимости деформаций:

(в)

Строго говоря, удлинение получится, если из точкиВописать дугу радиуса, однако, в силу малости деформаций,можно получить, опуская перпендикуляр из точкиА на новое направление стержня.

В собранном состоянии угол между стержнями будет меньше, чем. Однако, в силу малости деформаций, изменение углаотразится на 5 или 6 знаке косинуса, что несущественно.

3.Физическая сторона задачи.

Согласно закону Гука

Подставляя это в (в) получим:

(с)

4. Определение неизвестных.

Решая систему уравнений (с) и (а), с учетом, что N₁=R₁, аN₂=R₂имеем:

где N₁иN₂так называемые монтажные усилия.

 

Пример 23.

Определить усилия в стержнях системы, возникающие в результате поворота двухсторонней винтовой стяжки <<С>> на угол . Жесткость стяжки равна жесткости третьего стержня (рис. 2.50).

Дано: E₁=E₂=E₃=E,F₁=2F₃=2F₂=2F; шаг винтовой нарезки гайки-h;l₁=l.

Рис.2.50

 

Решение.

1.Статическая сторона задачи.

Составляем уравнения равновесия узла А(рис. 2.50, в). Учитывая симметрию относительно осиY, имеем:

отсюда (а)

Составляем уравнения равновесия узла B (рис. 2.50, с).

отсюда 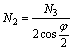(b)

Тогда степень статической неопределенности подсчитывается так: S=3-2=1

2. Геометрическая сторона задачи.

При повороте гайки на угол стержень 3, состоящий из двух частей, ввинтится в гайку на величину

Рис. 2.51

 

За счет ввинчивания стержня 3 точки А и В сблизятся на величину , а за счет растяжения этого стержня и стяжки они разойдутся на величину(рис. 2.51). Тогда, на основании схемы деформированной системы, ус­ловие совместности деформаций будет иметь вид:

(с)

3. Физическая сторона задачи.

Согласно закону Гука.

;;(d)

Здесь l₁=l₂по условию, аl₂иl₃можно определить из равенства проекций стержней на горизонтальную и вертикальную оси (рис. 2.50, а):

Подставляя (d) в (с), получим:

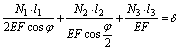(е)

4. Определение неизвестных.

Решая систему, составленную из уравнений (а), (в) и (е),получим:

 

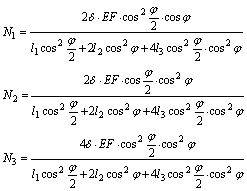
Пример 24.

Определить усилия в стержнях системы, возникающие в результате повышения температуры всех стержней на (рис. 2.52, а)

Дано: F₁=F₂=F; E₁=0,5E;E₂=E;;;l₁=l

Рис.2.52