1. Статическая сторона задачи.
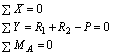
Первое и третье условия удовлетворялись тождественно. Таким образом, рассмотрение статической стороны задачи приводит к одному уравнению с двумя неизвестными
R1+R2=P(а)
Следовательно, данная задача один раз (S=2-1=1) статически неопределима и для ее решения нужно составить еще одно уравнение, содержащее те же неизвестныеR1иR2.
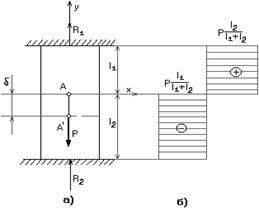
Рис.2.45
2. Геометрическая сторона задачи.
Установим связь между деформациями участков длиной l1иl2.
В случае неразрывности участок длинной l2укоротится на столько, насколько растянется участок длинойl1:
(b)
Это и есть условие совместности, выраженное в деформациях.
3. Физическая сторона задачи.
Для совместного решения (а) и(b)нужно, пользуясь законом Гука, выразить деформации(b)через усилия:
а т. к.N1=R1иN2=R2
то
отсюда
(с)
4. Определение неизвестных.
Решая (с)совместно с(а)получим:
Определив реакции опор, используя метод сечений, можно вычислить внутренние продольные силы. Эпюра продольных сил представлена на рис. 2.36, б.
5. Энергетическая проверка.
Работа А внешней силыРна
перемещении
равна сумме потенциальной энергии
деформацииUверхней
и нижней частей стержня:А=U
тогда
Учитывая, что
получим
или
т. е. равенство удовлетворяется.
Пример 19.
Определить продольные силы в стержнях,
на которых подвешена абсолютно жесткая
балка
,
нагруженная силой
(рис.2.46,а). Стержни изготовлены из
одного материала и имеют одинаковые
площади поперечного сечения. Длины
стержней равны
;
;
.
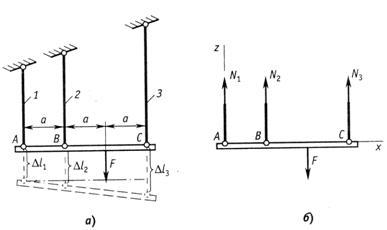
Рис.2.46
Решение.
Используя метод сечений, рассечем стержни и рассмотрим равновесие отсеченной части (рис.2.46, б). Составляем уравнение равновесия сил
;
;
.
Так как неизвестных сил три, а уравнений равновесия два, система один раз статически неопределима. Для решения задачи нужно составить одно уравнение совместности перемещений.
Рассмотрим геометрическую часть задачи.
Так как балка
по условию задачи абсолютно жесткая,
то в результате удлинения стержней она
переместится вниз и повернется на
некоторый угол, оставаясь прямолинейной.
Положение системы после деформации
стержней показано штриховыми линиями
на рисунке 2.46,а.
Составим уравнение, связывающее
перемещение сечений
,
и
стержней
,
откуда
.
Используя закон Гука, выразим перемещения через силы, действующие на стержни
или
.
Решив полученное уравнение перемещений совместно с уравнениями равновесия, найдем
;
;
.
Пример 20.
Определить продольные силы, возникающие в стержнях системы (рис.2.47, а). Материал, площади поперечных сечений и длины всех стержней одинаковы.
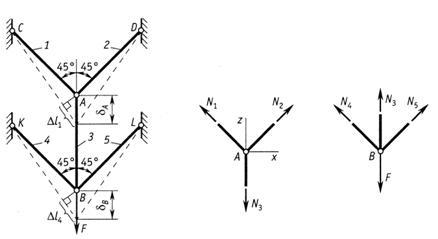
а) б)
Рис.2.47
Решение.
Применив метод сечений, вырезаем узлы
и
и, заменив действие отброшенных частей
системы силами (рис.2.47,б), составляем
уравнения равновесия сил для каждого
узла
для узла
,
откуда
;
;
для узла
,
откуда
;
.
Имеем четыре уравнения равновесия и пять неизвестных сил, следовательно, система один раз статически неопределима.
Рассмотрим геометрическую сторону
задачи. При нагружении системы силой
все ее стержни растягиваются и
деформированная система занимает
положение, показанное штриховыми линиями
на рисунке 2.47,а.
Если бы стержень 3был абсолютно
жестким, то при деформации системы
перемещения узлов
и
были бы одинаковыми. Так как стержень3растягивается, перемещение узла
больше перемещения узла
на удлинение этого стержня
.
Из схемы, представленной на рисунке 2.47, а, находим соотношение между перемещениями узлов и деформациями стержней
;
.
Запишем уравнение перемещений через деформации стержней
.
Используя закон Гука, выразим деформации стержней через действующие в них продольные силы
или
.
Решив полученное уравнение совместно с уравнениями равновесия, находим
;
;
.
Пример 21.
Определить усилия в стержнях системы, возникающие в результате действия силы Р. Деформациями массивной балкиАСпренебречь, рис.2.48.
Дано: E1=E2=E3=E;F1=2F2=2F3=2F;l1=l;l2=1,2l;l3=1,6l
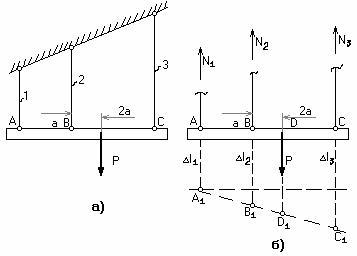
Рис.2.48
Решение.