209 Математическое приложение
МАТЕМАТИЧЕСКОЕ ПРИЛОЖЕНИЕ
В приложении дадим краткий обзор некоторых из математических понятий, используемых в тексте. Этот материал призван напомнить определения различных используемых в тексте терминов. Он ни в коем случае не является учебным материалом по математике. Определения, приведенные в приложении, как правило, простейшие и не самые строгие.
П.1 Функции
Функция есть правило, описывающее взаимосвязь между числами. Каждому числу x функция в соответствии с каким-либо правилом приписывает единственное число y. Поэтому функция может быть указана описанием правила, например, такого, как "возьмите число и возведите его в квадрат" или "возьмите число и умножьте его на 2" и т.д. Мы запишем эти конкретные функции как y = x21, y = 2x. Функции иногда называют трансформациями.
Зачастую мы хотим указать, что некоторая переменная y зависит от какой-то другой переменной x, но нам неизвестна конкретная алгебраическая связь между указанными двумя переменными. В этом случае мы записываем y = f(x), и эту запись следует истолковывать как утверждение о том, что переменная y зависит от x в соответствии с правилом f.
Если дана функция y = f(x), то число x часто называют независимой переменной, а число y — зависимой переменной. Идея состоит в том, что x изменяется независимым образом, а величина y зависит от величины x.
Часто некая переменная y зависит от нескольких других переменных x12, x23 и т.д., поэтому мы пишем y = f(x1, x2)4, чтобы показать, что величина y определяется обеими переменными совместно.
П.2 Графики
График функции описывает поведение функции с помощью рисунка. На рис.П.1 показаны два графика функций. В математике значения независимой переменной обычно откладываются на горизонтальной оси, а зависимой — на вертикальной оси. Тогда график показывает взаимосвязь между независимой и зависимой переменными.
В экономической теории, однако, принято при графическом изображении функций откладывать значения независимой переменной на вертикальной оси, а значения зависимой переменной — на горизонтальной оси. При графическом отображении функций спроса, например, цена обычно откладывается на вертикальной оси, а количество спроса — на горизонтальной оси.
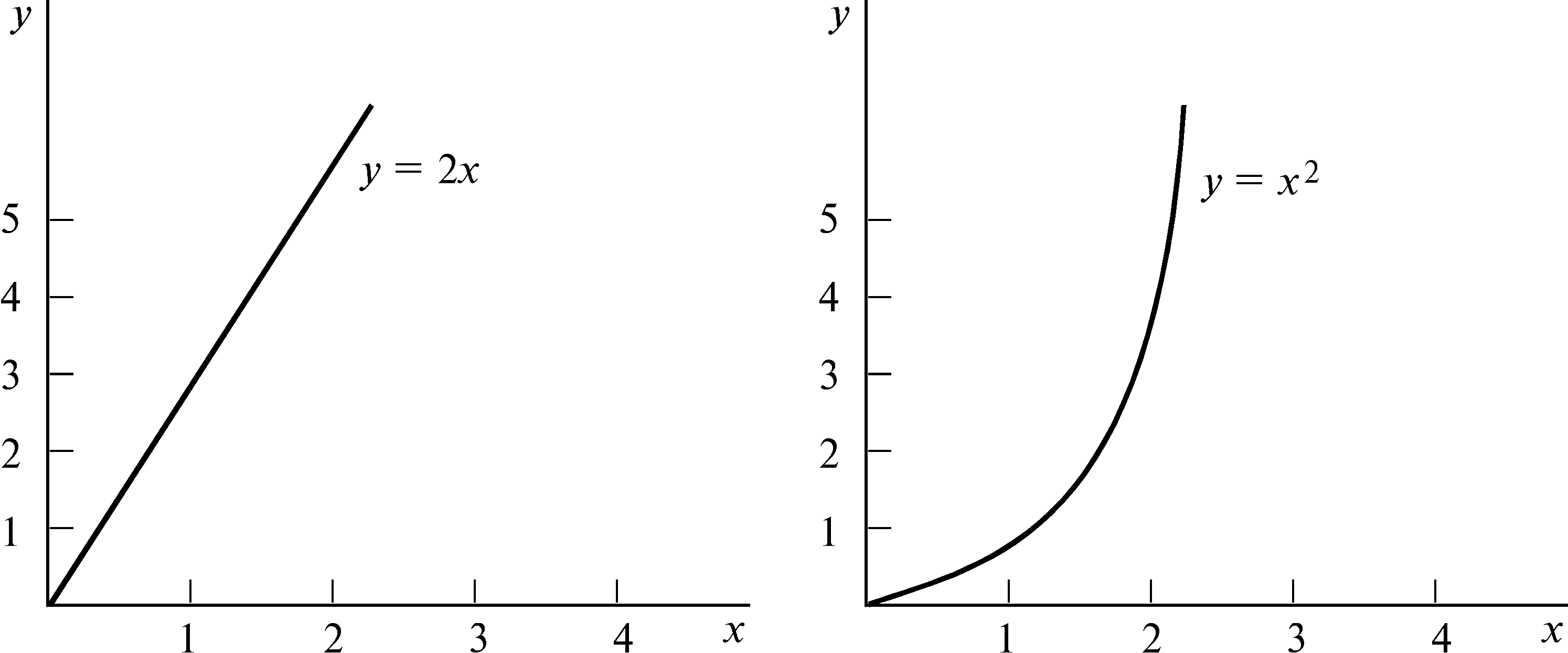
A B
|
Рис. П.1 |
Графики функций. Рис.A показывает график функции y = 2x, а рис.B — график функции y = x25. |
|
П.3 Свойства функций
Непрерывная функция есть функция, которую можно нарисовать, не отрывая карандаша от бумаги: у непрерывной функции нет скачков. Гладкая функция — это такая функция, у которой нет "изломов", или углов. Монотонная функция — функция, которая всегда возрастает или всегда убывает; положительная монотонная функция всегда возрастает с ростом x, в то время как отрицательная монотонная функция всегда убывает с ростом x.
П.4 Обратные функции
Как мы помним, функция обладает тем свойством, что для каждого значения x существует единственное связываемое с ним значение y и что монотонная функция есть функция, которая всегда возрастает или всегда убывает. Это означает, что для монотонной функции будет существовать единственное значение x, связываемое с каждым значением y.
Мы
называем функцию, связывающую x
c y
подобным образом, обратной
функцией.
Если вам задан y
как функция x,
вы можете вычислить обратную функцию,
просто выразив
x
как функцию y.
Если y
= 2x,
то обратная функция есть x
= y/2.
Если y
= x26,
то обратной функции не существует; при
любом y
как x=
+
7,
так и x=
—
8
обладают тем свойством, что их квадрат
равен y.
Поэтому не существует единственного
значения x,
связываемого с каждым значением y,
как того требует определение функции.