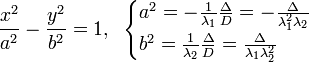39.​ Канонические уравнения и вид кривых второго порядка.

Вид кривой	Каноническое уравнение	Инварианты
Невырожденные кривые ()
Эллипс
Гипербола
Парабола
Вырожденные кривые ()
Точка
2пересек. прямые
2 паралл.прямые
Одна прямая

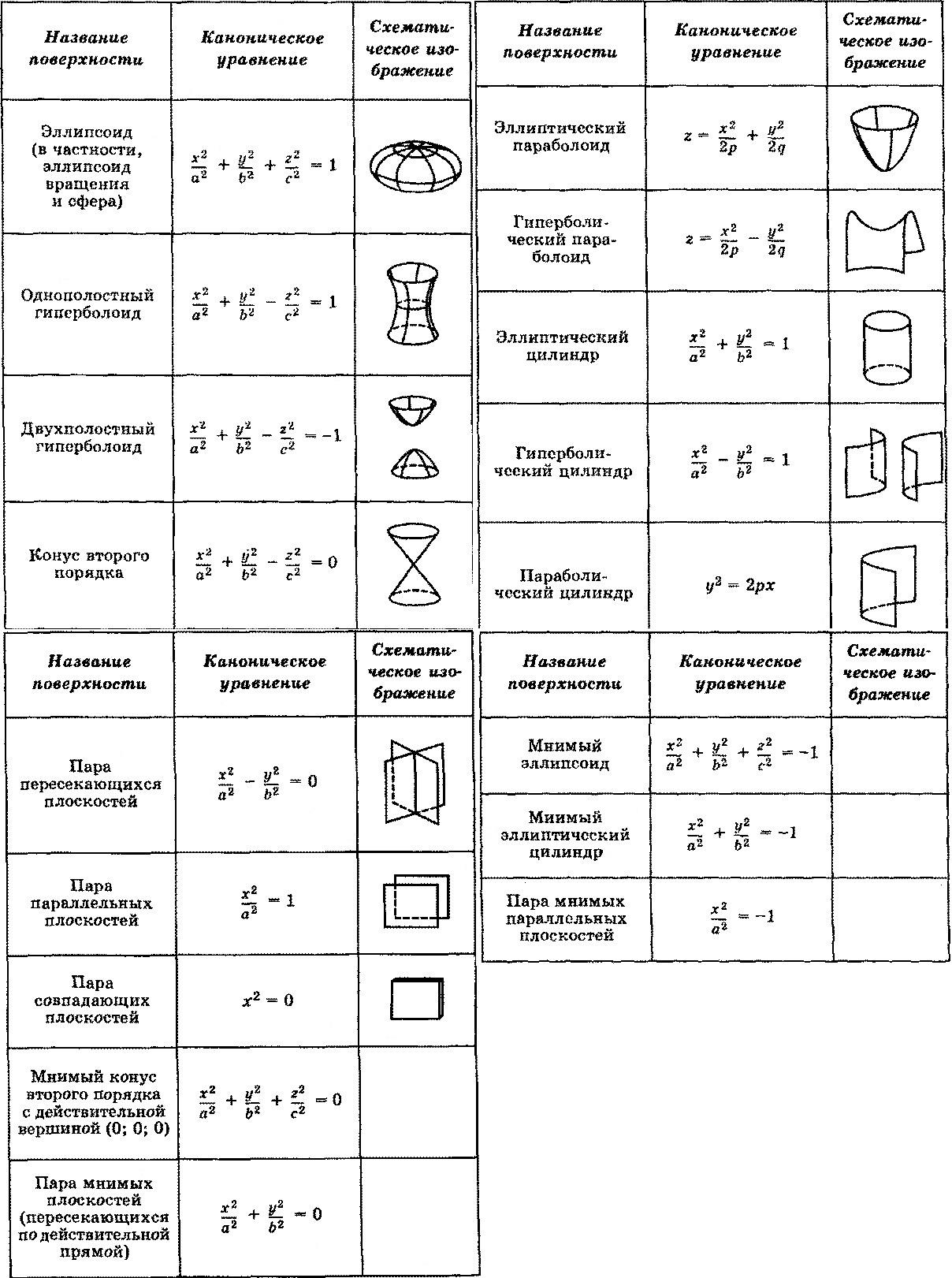
Для центральной кривой в каноническом виде её центр находится в начале координат.

40.​ Поверхности второго порядка.

Поверхность 2го порядка - геометрическое место точек 3хмерного пр-ства,

прямоугольные координаты которых удовлетворяют ур-нию вида:

Аффинное подпространство - подмн-во векторного пр-ва , явл. сдвигом какого-либо его линейного подпр-ва , т.е. мн-во вида при некотором .

Мн-во определяет однозначно, тогда как определяется только с точностью до сдвига на вектор из .Размерность определяется как размерность подпр-ва .

Аффинное подпр-во, кот. соответствует подпр-во коразмерности 1, наз. гиперплоскостью..

Аффинная система координат (косоугольная сист. координат) - прямолинейная система координат в аффинном пр-ве.

В -мерном пр-ве она задаётся упорядоченной системой линейно независимых векторов , выходящих из 1ой т. . Аффинными координатами т. наз. такие числа , что

T. и сист. вект. называют репером (аффинным базисом); прямые, проходящие через вектора  - координатными осями.

На аффинной плоскости координату называют абсциссой, а  -ординатой т. . В пр-ве же координаты т. наз. её абсциссой, ординатой и аппликатой. Аналогичным образом именуют и координатные оси.

метод Лагранжа

Данный метод состоит в последовательном выделении в квадратичной форме полных квадратов. Пусть есть данная квадратичная форма. Возможны 2 случая:

хотя бы один из коэффициентов при квадратах отличен от 0. Не нарушая общности, будем считать (этого всегда можно добиться соответствующей перенумерацией переменных);

все коэффициенты , но есть коэффициент , отличный от 0 (для определённости пусть будет ).

В 1ом случае преобразуем квадратичную форму следующим образом:, где, а через обозначены остальные слагаемые.  представляет собой квадратичную форму от n-1 переменных .

С ней поступают аналогичным образом и так далее. Заметим, что  . 2ой случай заменой переменных сводится к 1ому.