Математическая статистика

Билет 1

Задачи математической статистики. Выборочный метод. Вариационные ряды. Графическое представление вариационного ряда.

Первая задача математической статистики – указать способы получения, группировки и обработки статистических данных, собранных в результате наблюдений, специально поставленных опытов или произведённых измерений.

Вторая задача математической статистики – разработка методов анализа статистических сведений в зависимости от целей исследования.

Случайную величину будем называтьгенеральной совокупностью .

Исходным материалом для изучения свойств генеральной совокупности являются статистические данные, т.е. значения, полученные в результате повторения случайного опыта (измерения случайной величины). Предполагается, что опыт может быть повторён сколько угодно раз в неизменных условиях. Это означает, что распределение случайной величины,, заданной на множестве исходов-го опыта, не зависит оти совпадает с распределением генеральной совокупности.

Набор независимых в совокупности случайных величин, гдесоответствует-му опыту, называют случайной выборкой из генеральной совокупности . Числоназываетсяобъёмом выборки.

Совокупность чисел , полученных в результате-кратного повторения опыта по измерению генеральной совокупности, называетсяреализацией случайной выборки или просто выборкой объёма .

В основе большинства результатов математической статистики лежит выборочный метод, состоящий в том, что свойства генеральной совокупности устанавливаются путём изучения тех же свойств на случайной выборке.

Вариационный ряд

Простейшее преобразование статистических данных является их упорядочивание по величине.

Выборка объёмаиз генеральной совокупности, упорядоченная в порядкенеубывания элементов, т.е. , называетсявариационным рядом:

.

В том случае, когда объем наблюдений выборки небольшой, находят разные наблюдения и указывают их частоту. Полученные данные записывают в так называемую таблицу частот дискретного вариационного ряда следующего вида:

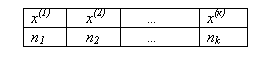
Таблица, в которой приведены все интервалы с соответствующими частотами по интервалам для заданной выборки наблюдений, называется таблицей частот интервального вариационного ряда.

Распределения частот и относительных частот по интервалам можно представить не только в виде таблиц, но и графически. Графическое изображение данных интервального вариационного ряда строят в виде гистограммы частот или полигона частот.

Гистограмма частот изображается так: над каждым интервалом строится прямоугольник, основанием которого служит данный интервал, а высотой – частота в данном интервале. Как правило, для удобства рассмотрения единицы масштаба по оси абсцисс и по оси ординат выбираются разными. Кроме того, и начала отсчета по разным осям тоже могут не совпадать. Гистограмма частот для рассматриваемого примера показана на рис.1.

Если по оси ординат откладывать не частоты в интервалах, а относительные частоты в интервалах, то подобным образом можно построить гистограмму относительных частот.

Полигон частот для интервального вариационного ряда изображается так: в середине каждого интервала строится ордината, равная частоте на этом интервале, и концы ординат соединяются. Полигон частот для рассматриваемого примера показан на рис.2.

Если же строить в середине каждого интервала ординату, равную относительной частоте на этом интервале, и соединить концы ординат, то получим полигон относительных частот.

Билет 2

Выборочные оценки числовых характеристик.

Оценка числовых характеристик и параметров распределения(Несгруппированные результаты)После отбрасывания всех сомнительных результатов ряд содержитnизмеренийx_i(где i= 1, 2, 3, …,n), некоторые из которых могут иметь одинаковое значение. Математическое ожидание представляемого этим рядом нормального распределения оценивается средним арифметическимдля результатов:, (4)Оценка стандартного отклонения(Несгруппированные результаты) Стандартное отклонение по квадратам отклонений результатов измерений от среднего арифметического определяется по формуле:, (7) гдеx- значениеi-го измерения (i= 1, 2, 3, …,n);n- общее число измерений;- среднее арифметическое n измерений, вычисленное в соответствии с п. 6.1.1. Чтобы облегчить вычисление, рекомендуется следующая формула: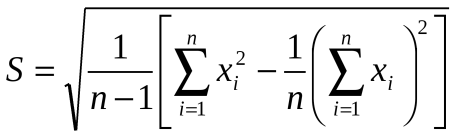. (8) Вычисление выборочных характеристик при малом объеме выборки6.3.1 Выборочное среднееопределяется в соответствии с п. 6.1.1. 6.3.2 Выборочная медиана при нечетном объеме выборкиn = 2m – 1равна среднему члену вариационного рада Х_0,5= Х_m. При четном объемеn = 2mмедиана равна среднему значению двух средних значений вариационного ряда:. (11) 6.3.3 Выборочная дисперсия D = S²=, (12) или D =[Σ x²_i-(Σx_i)²] . (13) Вычисление выборочных моментов третьего и четвертого порядков при объеме n<50 нецелесообразно в связи с их большими вероятными отклонениями от генеральных моментов. Для нормально распределенной генеральной совокупности оценки среднего, дисперсии являются эффективными, состоятельными и несмещенными. Несмещенная оценка СКО: S=k*s, где k – поправочный коэффициент, зависящий от объема выборки (Приложение Б).

Билет 3

Выборочная функция распределения.

Понятие выборочной функции распределения F_n(x).

Пусть таблица дискретного вариационного ряда имеет вид:

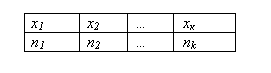
где х₁ < х₂ <…< х_k, 1 ≤ k ≤ n, n₁- частота х₁, n₂> – частота х₂,…, n_k> – частота х_k, причем n₁+n₂+…+n_k=n.

Выборочной функцией распределения F_n(x)> называется ступенчатая функция следующего вида:

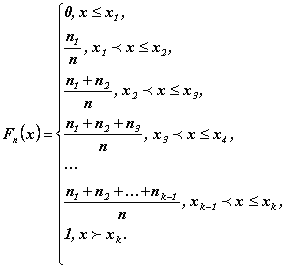
Выборочная функция F_n(x) является постоянной на каждом интервале (х_р, х_р+1), а в каждой точке х_р увеличивается на величину n_р /n , р=1,2,…, k-1. Кроме того, F_n(x) – неубывающая функция, 0 ≤ F_n(x) ≤ 1, F_n(-∞)=0, F_n(+∞)=1.

Билет 4

Понятие оценки числовой характеристики или параметра распределения. Свойства точечных оценок. Выборочная оценка математического ожидания, ее свойства