Билет 1

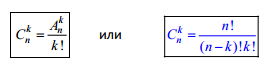
Основное правило комбинаторики. Перестановки, размещения, сочетания.

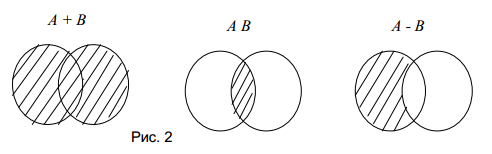
Билет 2 Классификация событий. Пространство элементарных событий. Действия над событиями. Свойства операций над событиями. Диаграммы Венна.

Действия над событиями.

Диаграммы Венна

Билет 3 Классическое определение вероятности события, свойства вероятности; статистическое определение вероятности. Теорема Бернулли.

Статистическое определение вероятности. Вероятностью события  называется число, относительно которого стабилизируется (устанавливается) относительная частота  при неограниченном увеличении числа опытов.

В практических задачах за вероятность события  принимается относительная частота  при достаточно большом числе испытаний

.

Формула Бернулли

Пусть производится  независимых испытаний, в каждом из которых событие  может появиться либо не появиться. Кроме того, будем предполагать, что вероятность события в каждом отдельном испытании одна и та же и равна  (соответственно, вероятность того, что событие  в каждом отдельном испытании не наступит, также постоянна и равна ). Тогда вероятность того, что событие  в  независимых испытаниях произойдет ровно  раз, равна . Данная формула называется формулой Бернулли.

!!!(Есть еще теорема Бернулли (ниже), но я все же думаю, что он эту формулу имел в виду)

Билет 4

Теорема сложения вероятностей. Условная вероятность. Теорема умножения вероятностей.

Билет 5 Формула полной вероятности. Формула Байеса.

6. Биномиальная схема испытаний. Формула Бернулли, наиболее вероятное число успехов.

Теорема(формула Бернулли). Обозначим через Pn(m) вероятность того, что событие А наступило m раз в n испытаниях. Вероятность Pn(m) определяется формулой

Pn(m) = C_n^m *p^m *q^n-m

Определение. Число наступлений события А называется наивероятнейшим, если оно имеет наибольшую вероятность по сравнению с вероятностями наступления события А любое другое количество раз. Наивероятнейшее число m0 наступлений события А в n испытаниях заключено в интервале np - q <= m₀ <=np + p Если np- q −целое число, то наивероятнейших числа два np - q и np+ p .

6. Приближенные формулы Муавра-Лапласа и Пуассона.

Предположим, что мы хотим вычислить вероятность Pn (m) появления события A при большом числе испытаний n. Ясно, что в этом случае непосредственное вычисление по формуле Бернулли технически сложно, тем более, если учесть, что сами p и q – числа дробные. Поэтому возникает естественное желание иметь более простые, пусть даже и приближенные, формулы для вычисления Pn (m) при больших n.

Наиболее известными являются формулы Пуассона и Муавра- Лапласа.

Теорема Муавра-Лапласа (локальная). Если вероятность наступления события А в каждом из n независимых испытаниях равна р и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность Pn (m), того, что в n испытаниях события А наступит m раз, приближенно равна

P= (1/√(npq))*φ(x), где x=(m-np)/√(npq) , а функция φ – функция Гаусса(см. в таблице значений) ϕ(x) является четной, ϕ(x) –монотонно убывающая при положительных значениях x и при x>4 функция приближенно равна 0.

Теорема Муавра-Лапласа (интегральная). Если вероятность наступления события А в каждом из n независимых испытаниях равна р и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность того, что в n испытаниях число успехов m находится между m1 и m2 приближенно равна

P(m1<m<m2)=1/2(Ф(x2) – Ф(x1)), где x_i = (m_i-np)/√(npq) и i=1,2. нечетная функция.

Теорема (Пуассона). Предположим, что произведение np остается постоянной величиной, когда n неограниченно возрастает. Обозначим λ = np. Тогда для любого фиксированного m и любого постоянного λ:

В случае, когда n велико (n >100), а р мало ( p < 0,1), причем npq ≤ 9, вместо формулы Бернулли применяют приближенную формулу Пуассона

, Где λ = np.