ФМФ-2 Методы оптимальных решений

ВСЕ БИЛЕТЫ!!!!

Билет 1. Общая постановка задач математического программирования. Различные формы задач линейного программирования, связь между ними.

Линейное программирование – направление математики, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием оптимальности.

Круг задач:

-задача об оптимальном использовании ресурсов при производственном планировании;

-задача о смесях (планирование состава продукции);

-задача о нахождении оптимальной комбинации различных видов продукции для хранения на складах (управление товарно-материальными запасами или "задача о рюкзаке");

-транспортные задачи (анализ размещения предприятия, перемещение грузов).

Экономико-математическая модель любой задачи линейного программирования включает: целевую функцию, оптимальное значение которой (максимум или минимум) требуется отыскать;ограничения в виде системы линейных уравнений или неравенств; требование неотрицательности переменных.

Общая форма задачи линейного программирования.

Задана система m линейных ограничений с n переменными:

a₁₁x₁ + a₁₂x₂ +… + a_1nx_n≤ (≥) b₁,

a₂₁x₁ + a22x2 +… + a2nxn≤ (≥) b₂,

…………………... ... ... ... ... ... ...,

a_k1x1 + ak2x2 +… + aknxn≤ (≥) b_k,

a_k+1,₁x₁ + a_k+1,2x₂ +… + a_k+1,nx_n = b_k+1,

a_k+2,₁x₁ + a_k+2,2x₂ +… + a_k+2,nx_n = b_k+2,

… … … … … … … ... ... ... ... ... ... ...,

a_m1x₁ + a_m2x₂ +… + a_mnx_n = b_m,

где: x₁≥ 0, x₂≥ 0,…, x_n≥0,

а линейная функция Z = c₁x₁ + c₂x₂ +… + c_nx_n→mаx (min).

Необходимо найти переменные x1, x2,…, xn, которые удовлетворяют системе ограничений и приводят целевую функцию к максимальному или минимальному значению. В общей форме задачи линейного программирования система ограничений включает в себя как равенства, так и неравенства, а целевая функция может стремиться как к максимуму, так и к минимуму.

Стандартная форма задачи линейного программирования:

a₁₁x₁ + a₁₂x₂ +… + a_1nx_n≤ (≥) b₁,

a₂₁x₁ + a₂₂x₂ +… + a_2nx_n≤ (≥) b₂,

… … … … … … … … … ... ...,

a_m1x₁ + a_m2x₂ +… + a_mnx_n≤ (≥) b_m,

где: x₁≥ 0, x₂≥ 0,…,x_n≥0,

а линейная функция Z = c₁x₁ + c₂x₂ +… + c_nx_n→ mаx (min)

Особенность данной формы состоит в том, что в ней система ограничений состоит из одних неравенств, переменные решения являются неотрицательными, а целевая функция может стремиться как к максимуму, так и к минимуму.

Каноническая форма задачи линейного программирования:

Форма, в которой Z = c₁x₁ + c₂x₂ +… + c_nx_n→mаx,

a₁₁x₁ + a₁₂x₂ +… + a_1nx_n = b₁,

a₂₁x₁ + a₂₂x₂ +… + a_2nx_n = b₂,

… … … … … … … … … ...,

a_m1x₁ + a_m2x₂ +… + a_mnx_n = b_m,

все переменные неотрицательные: x1≥ 0, x2≥ 0,…, xn≥ 0, система ограничений представляет собой систему уравнений, а целевая функция стремится к максимуму.

Билет 2. Примеры задач линейного программирования.

Производственная задача

сырьё	Норма расхода на 1 кг			Запасы
	Карамель 1	2	3
сах. песок	0,8	0,5	0,6	80
патока	0,4	0,4	0,3	60
фрукт. пюре	-	0,1	0,1	12
прибыль	1080	1120	1260
	x1	x2	x3

0,8x1 + 0,5x2 + 0,6x3 ≤ 80

0,4x1 + 0,4x2 + 0,3x3 ≤ 60

0,1x2 + 0,1x3 ≤ 12

x1, x2, x3 ≥ 0

z = 1080x1 + 1120x2 + 1260x3 → max

Задача о диете

	в 100гр продукта	Норма потребления			min	max
	масло	мясо	хлеб	сок
калории	800	280	245	80	2400	2800
белок	0,6	16	8	0	60	60
жир	20	5	0	0	0	30
углеводы	0	0	5	10	10	40
холестерин	0,16	0,08	0	0	0	0,5
цена	30	40	5	10
	х1	х2	х3	х4

2400 ≤ 800x1 + 280x2 + 246x3 + 80x4 ≤ 2800

0,6x1 + 16x2 + 8x3 = 60

0 ≤ 20x1 + 5x2 ≤ 30

10 ≤ 5x3 + 10x4 ≤ 40

0 ≤ 0,16x1 + 0,08x2 ≤ 0,5

x1, x2, x3, x4 ≥ 0

z = 30x1 + 40x2 + 5x3 + 10x4 → min

Транспортная задача

В пунктах А1, …, Аm производится продукт в количествах a1, …, am

В пунктах B1, …, Bn продукт потребляют в количествах b1, …, bn

Дана C = (cij) mxn

cij – стоимость перевозки единицы товара от Ai к Bj

Требуется:

1) От каждого Ai все вывезти;

2) Заявку каждого Bj выполнить;

3) Минимизировать общую стоимость перевозки;

Переменные:

xij – количество товара, перевозимого от Ai к Bj

ai = xi1 + … + xin 1 ≤ i ≤ m

bj = x1j + x2j + … + xmj 1≤ j ≤ n

xij ≥ 0

z = ∑ xijcij → min

Теорема. Транспортная задача имеет решение тогда и только тогда, когда ∑ai = ∑bi.

Задача о раскрое

45см х 90 (х1)

50см х 96 (х2)

65см х 88 (х3)

85см х 56 (х4)

а) → min общими отходами

184 = 4 х 45 х1

184 = 3 х 50 х2

184 = 2 х 65 х3

184 = 2 х 85 х4

4х1 ≤ 90

3х2 ≤ 96

2х3 ≤ 88

2х4 ≤ 56

х1, х2, х3, х4 ≥ 0

z = 4x1 + 3x2 + 2x3 + 2x4 → min

б) потребление min количества листов

x1, x2, x3, x4 ≥ 0

x1, x2, x3, x4 - целые

x1 + x2 + x3 + x4 → min

Билет 3. Геометрическая интерпретация условий задач линейного программирования. Выпуклые многогранные мн-ва: свойства решений систем линейных неравенств.

Сведение к симплексной форме:

x1 + x2 ≤ 1

x1 – 3x2 ≥ -3

Сведение к неотрицательным переменным:

x1= y1 – y2; yi, zj ≥ 0

x2 = z1 – z2

y1 – y2 + z1 – z2 ≤ 1

y1 – y2 – 3z1 + 3z2 ≥ -3

y1, y2, z1, z2 ≥ 0

Процесс выравнивания:

y1 - y2 + z1 – z2 + t1 = 1

y1 – y2 -3z1 + 3z2 – t2 = -3

y1, y2, z1, z2, t1, t2 ≥ 0

Свободные члены ≥0

y1 – y2 + z1 – z2 + t1 = 1 Симплексная форма

-y1 + y2 + 3z1 – 3z2 + t2 = 3

y1, … t2 ≥ 0

Условия, характ. симплексную форму:

а) неизвестные ≥ 0

б) ограничение уравнения

в) свободные члены ≥ 0

Прямая задача линейного программирования

а11 х1 + … + а1n xn ≤ b1

an1 x1 + … + amn xn ≤ bm

x1, …, xn ≥ 0

z= p1 x1 + … + pn xn -> max

Опр. Подмножество М в Rⁿ выпукло, если из А, В ∈ М => [А ; B] ∈ М

Т. С-ма неравенства прямой задачи ЛП задает замкнутое выпуклое мн-во.

Опр. Подмножество М в Rⁿ замкнуто, если предел любой сходящейся последовательности из М содержатся в М.

Т. Если с-ма неравенства прямой задачи ЛП имеет ограниченное мн-во решений. То задача ЛП имеет решение.

Опр. Вершина в прямой задачи.

Выберем из всех неравенство n неравенство. Превратим их в уравнение. Получается с-ма из n уравнений с n неизвестными. Пусть оно имеет ед. решение,, которое удовлетворяет отсальным неравенствам. Тогда это решение наз. Вершиной.

Т. Max z, если он существует, достигается в вершине.

Выпуклым многогранным множеством (ВММ)-назыв. пересечение семейства

полупространств.

Х ∈ Ω назыв. угловой точкой (вершиной) выпуклого многогранного множества Ω, если

она не является внутренней точкой какого-либо отрезка с концами в Ω:

Задание выпуклого многогранника с помощью уравнений и неравенств.

Пусть грани выпуклого многогранника лежат в плоскостях, задаваемых уравнениями

Y

Тогда сам многогранник является пересечением соответствующих полупространств и,следовательно, для его точек должна выполняться система неравенствY которая и определяет этот многогранник.

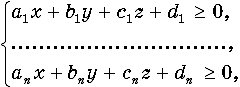
Билет 4. Двойственность в линейном программировании: правило перехода, основная теорема.

Прямая задача ЛП Двойственная задача

a11 x1 + … + am xn ≤ b1 y1a1 + … + yn am1 ≥ p1

am1 x1 + … + amn xn ≤ bm y1an + … + yn amn ≥ pn

x1, …, xn ≥ 0 y1…yn ≥ 0

z= p1x1 + pnxn -> max t = b1y1 + … + bm ym -> min

a11 …… am1 p1 a11 ….. a1n b1

……………………….. -------> ………………………….

a1n…….amn pn am1…..amn bm

b1………bn 0 p1……..pn 0

Теорема: пусть неравенства в прямой задаче и в двойственной задаче имеют решения. Тогда обе задачи имеют решение и ответы совпадают ( max z = min t)

Билет 5. Теорема о равновесии, ее примени и интерпретации, вопрос о дефиците.

Пусть х^* = ( x^*1, …. х^*n) – точка макс z

Y^* = ( y^*1, …, y^*m) – точка мин t

Тогда ∀j = 1, …, m ∀i=1, …, n

y^*j ( aj1x^*1 + … + ajn x^*n – bi) = 0 y^*I ( y^*1a1i + … + y^*ma mi)=0

Пусть y^*j >0

Aj1x^*1 + … + ajnx^*n = bj

Дает возможность найти вершину х*, ulе достигается макс z

y^*j>0 => j-ый ресурс будет полностью израсходован

Вопрос о дефиците( из производственной задачи):

I(x₁) II(x₂) Запас

Товары R₁ 0,5 0,7 100

R₂ 0,6 0,4 200

R ₃ 0,3 0,5 150 Отпускная 10 20

цена

0,5x₁ + 0,7x₂ ≤ 100 Оказалось, что y_j*> 0, что,

0,6x₁ + 0,4x₂ ≤ 200 что jый ресурс будет израсход.

0,3x₁ + 0,5x₂ ≤ 150 полностью.

z= 10x₁+20x₂ max

Билет 6. Математическая модель транспортной задачи. Условия разрешимости.

В пунктах А1, …, Аm производится продукт в количествах а1, …,аm. В пунктах B1, …, Bn продукт потребляется в количествах в1, …, вn

Дано С= ( сij) myn ; Cij – стоимость перевозки единицы товара от Аi к Bj

Требуется:

а) от каждого Аi все вывести

б) заявку каждого Bj выполнить

в) минимизировать общую стоимость перевозки

Переменные:

Xij – кол-во товара, перевозимого от Аi к Bj

ai = Xi1 + Хin; j≤ I ≤ m

bj = X1j + X2j + … + Xmj; i≤ j ≤ n

xi j≥ 0 z=

Т: транспортная задача имеет решение тогда и только тогда =

Общая постановка транспортной задачи состоит в определении оптимального плана перевозок некоторого однородного груза из m пунктов отправления (производства)  в n пунктов назначения (потребления) . При  этом в качестве критерия оптимальности обычно берется либо минимальная стоимость перевозок всего груза, либо минимальное время его доставки. Рассмотрим транспортную задачу, в качестве критерия оптимальности которой взята минимальная стоимость перевозок всего груза. Обозначим через  тарифы перевозки единицы груза из i-го пункта отправления в j-й пункт назначения, через  – запасы груза в i-м пункте отправления, через  – потребности в грузе в j-м пункте назначения, а через  – количество единиц груза, перевозимого из i-го пункта отправления в j-й пункт назначения.

        Составим математическую модель задачи. Найти наименьшее значение линейной функции

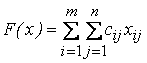(12.1)

при условиях

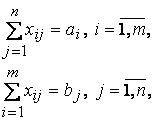
 (12.2)

Пункты отправления	Пункты назначения					Запасы
				…
				…
				…
…	…	…	…	…	…	…
				…
Потребности				…

        План , при котором функция (12.1) принимает свое минимальное значение, называется оптимальным планом транспортной задачи. Обычно исходные данные транспортной задачи записывают в виде таблицы.

Теорема Для разрешимости транспортной задачи необходимо и достаточно, чтобы запасы груза в пунктах отправления были равны потребностям в грузе в пунктах назначения, т. е. чтобы выполнялось равенство

(12.3)

Модель такой транспортной задачи называется закрытой, или замкнутой, или сбалансированной, в противном случае модель называется открытой.

       В случае 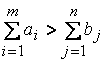 вводится фиктивный (n + 1)-й пункт назначения с потребностью  и соответствующие тарифы считаются равными нулю: аналогично, при 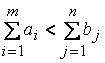 вводится фиктивный (m + 1)-й пункт отправления с запасом груза 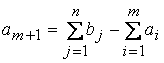 и тарифы полагаются равными нулю:.

Этим задача сводится к обычной транспортной задаче. В дальнейшем будем рассматривать закрытую модель транспортной задачи. Число  переменных    в  транспортной  задаче  с  m  пунктами  отправления  и  n  пунктами  назначения  равно mn, а число уравнений в системе (12.2)   m + n. Так  как  мы предполагаем выполнение условия (12.3), то число линейно независимых уравнений равно m + n – 1. Следовательно, опорный план может иметь не болееm + n – 1 отличных от нуля неизвестных. Если в опорном  плане  число отличных от  нуля  компонент равно в точности m + n – 1, то план называется невырожденным, а если меньше – то вырожденным.

Билет 7. Выпуклые, вогнутые и однородные функции.

f1(x)≥0 x=(x1,…, xm)

fm(x)≥0 f(x) – выпуклая функция

z max

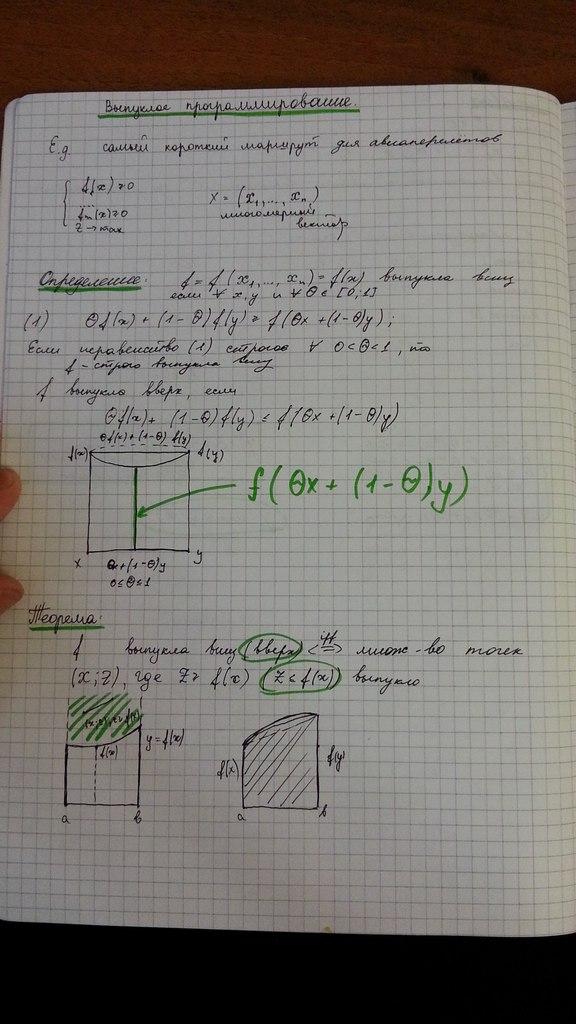
f=f(x1,…., xm)= f(x) выпукла вниз, если ∀ x,y и ∀ θ ∈ {0;1]

θf(x)+(1- θ)f(y)≥f(θx+(1- θ)y

Если неравенство строгое ∀ 0< θ <1, то f строго выпукла вниз

f выпукла вверх (вогнута), если θf(x)+(1- θ)f(y)≤f(θx+(1- θy)

θf(x)_+(1- θ)f(y)

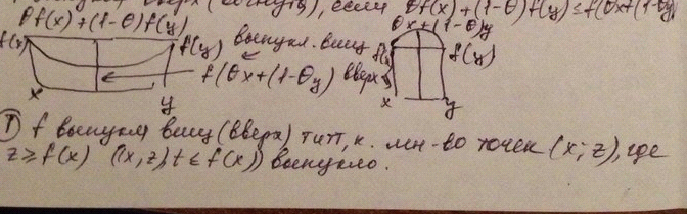
Билет 8. Достаточные условия второго порядка выпуклости функции.

Теорема. (Достаточное условие выпуклости)

Пусть y = f (x) непрерывна на [a,b], и имеет в (a, b) производную до второго порядка включительно, тогда

а) если во всех точках интервала (a, b) вторая производная функции f (x) отрицательна f '' (x) < 0, то кривая на (a, b) выпукла вверх;

b) если во всех точках интервала вторая производная положительна f '' (x) > 0, то кривая на (a, b) выпукла вниз.

Доказательство. Если f''(x)>0, x X, то f'(x) возрастает на множестве X и по предыдущей теореме функция выпукла вниз на множестве X. Аналогично рассматривается случай, когда f''(x)<0

Билет 9. Постановка задачи выпуклого программирования. Метод Лагранжа. Необходимые условия экстремума

Задача выпуклого программирования - задача оптимизации, целевая функция и допустимое множество которой – выпуклые. Общая задача В. п. состоит в отыскании такого вектора x (т. е. такой точки выпуклого допустимого множества), который доставляет минимум выпуклой функции f(x) или максимум вогнутой функции y(x). Выпуклость (вогнутость) важна тем, что гарантирует нахождение оптимального решения задачи, так как соответственно локальные и глобальный экстремумы здесь обязательно совпадают. Критериями оптимальности в первом случае могут быть, напр., издержки при различных сочетаниях факторов производства, во втором случае — величина прибыли при этих сочетаниях.

Теорема (Необходимое условие экстремума) Если функция нескольких переменных u = f(x1, x2, … , xn) имеет экстремум в некоторой точке, то в этой точке каждая ее частная производная равна нулю или не существует.

Билет 10. Достаточные условия экстремума в случае, когда ограничения заданы уравнениями.

Билет 11. Достаточные условия экстремума в случае, в случае, когда ограничения заданы неравенствами. Условия Куна-Такера.

max f(x)

g1(x) ≤C₁

…………….

g_k(x) ≤ C_k

α=f(x)-_j(g_j(x)-C_j)

Теорема: если х – точка локального max, то в ней для некоторого набора α₁,…, α_k ≥0

α’_x1=…= α’_xn = 0 α’_x1 = α’_x2 = 0

α _j(g_j(x)-C_j) = 0 α ₁(g₁(x)-C₁) = 0

α _j ≥ 0 => α ₁ ≥ 0

g_j(x) ≤C_j g₁(x) ≤C₁

j=1,…k

Достаточное условие максимума. Условие Куна-Таккера

f(x)-> max

g1(x) ≤r₁

…………….

g_k(x) ≤ r₂

x≥0

Условия Куна-Таккера

α_x1 ≤ 0, …, α’_xn≤ 0 α’_α1 ≤ 0, …, α’_αn ≥ 0

x₁ ≥ 0, …, x_n ≥ 0 α ₁ ≥ 0, …, α _n ≥ 0

x_1*α’_x1 = 0, …, x_n*α’_xn = 0 α _1*α’_α1 = 0, …, α _n*α’_αn = 0

Если х удовлетворяет этим условиям, то это будет точка максимума.

Билет 12. Решение задачи потребительского выбора.

Билет 13. Конечные антагонистические игры. Верхняя и нижняя цена игры.

Билет 14. Принцип доминирования.

Билет 15 и 16. Вальд. Игры с природой и Севидж. (все в кучу)

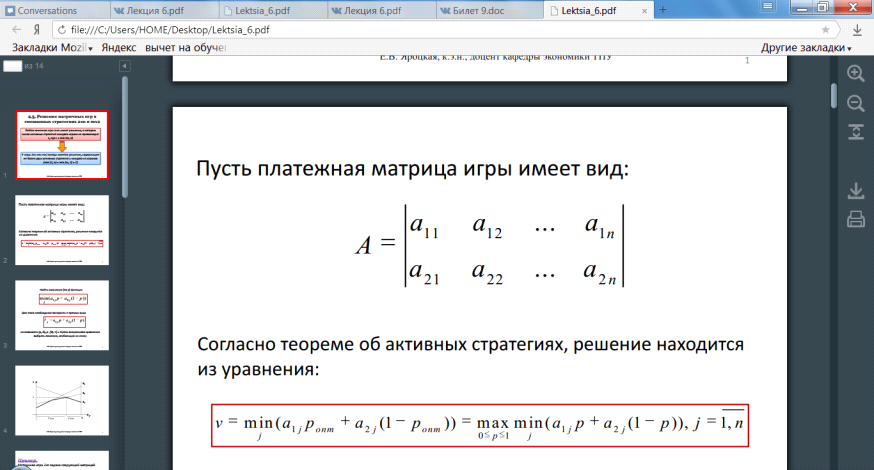
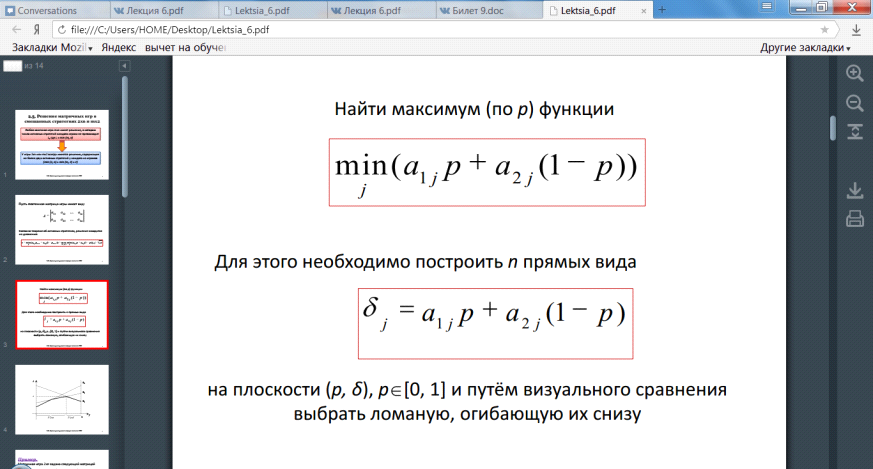
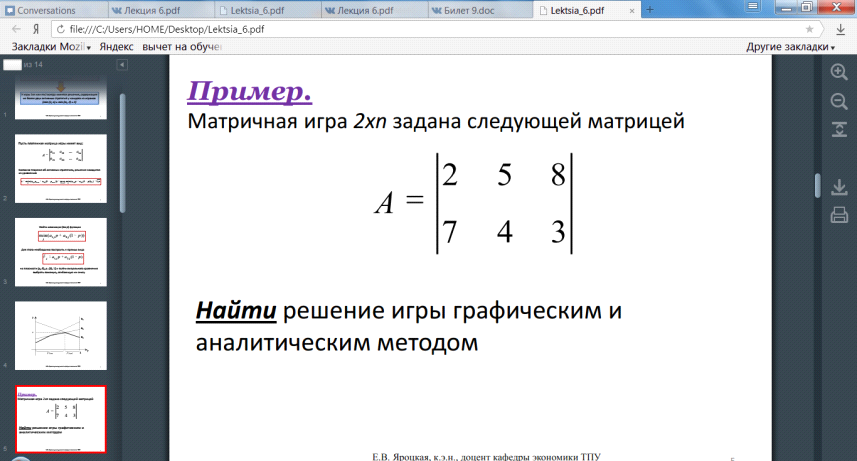
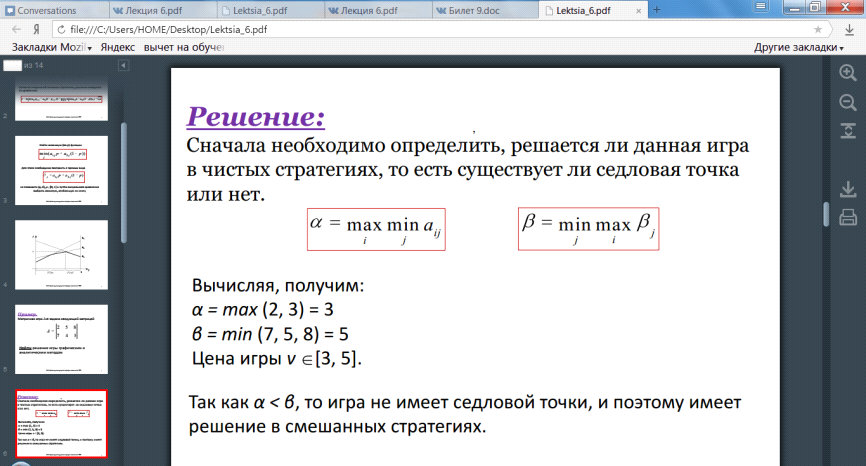
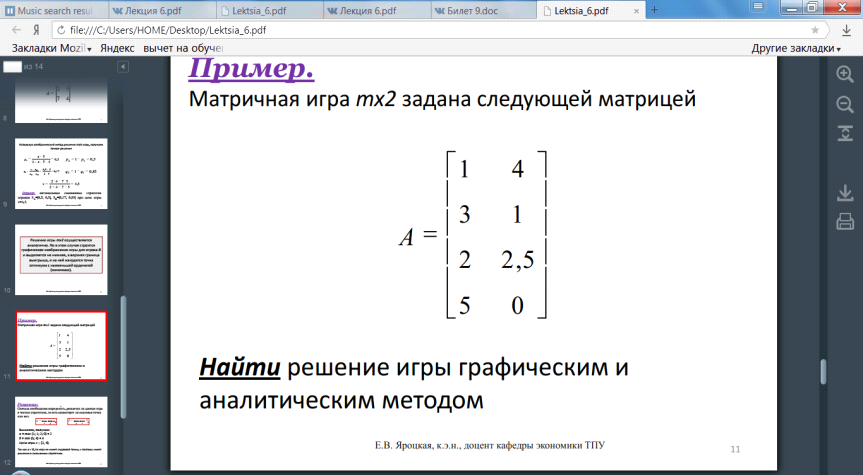
Решение матричных игр в смешанных стратегиях может быть найдено либо графически, либо методами линейного программирования. Методами линейного программирования может быть решена любая игра двух лиц с нулевой суммой.

Критерий Сэвиджа — один из критериев принятия решений в условиях неопределённости. Условиями неопределённости считается ситуация, когда последствия принимаемых решений неизвестны, и можно лишь приблизительно их оценить. Для принятия решения используются различные критерии, задача которых — найти наилучшее решение максимизирующее возможную прибыль и минимизирующее возможный убыток. Критерий заключается в следующем: Строится матрица стратегий (платёжная матрица). Столбцы соответствуют возможным исходам. Строки соответствуют выбираемым стратегиям. В ячейки записывается ожидаемый результат при данном исходе и при данной выбранной стратегии. Строится матрица сожаления (матрица рисков). В ячейках матрицы величина сожаления — разница между максимальным результатом при данном исходе (максимальном числе в данном столбце) и результатом при выбранной стратегии. Сожаление показывает величину, теряемую при принятии неверного решения. Минимальное решение соответствует стратегии, при которой максимальное сожаление минимально. Для этого для каждой стратегии (в каждой строке) ищут максимальную величину сожаления. И выбирают то решение (строку), максимальное сожаление которого минимально.

Билет 17.

Билет 18. Решение матричных игр в смешанных стратегиях.