
Lektsia_Zubchatye_peredachi_i_kolesa
.pdfМодуль «Нормирование точности зубчатых передач и колес»
Введение
В данном материале рассмотрим особенности нормирования зубчатых передач и колес, элементы расчета и конструирования. Данный материал связан с теорией мо-
дуля «Разъемные соединения. Нормирование точности шпоночных и шлицевых со-
единений».
Зубчатые механизмы являются наиболее распространенным в машиностроении и приборостроении видом механических передач. Такие передачи применяют для пере-
дачи вращательного движения с одного вала на другой или для преобразования вра-
щательного движения в поступательное и изменение скорости вращения валов.
Зубчатые передачи можно классифицировать по различным признакам.
По характеру расположения валов:
–с параллельными осями;
–с пересекающимися осями;
–с скрещивающимися осями.
По форме профилей зубьев:
–эвольвентные;
–циклоидальные;
–круговые и другие.
Передачи с внешним и внутренним зацеплением.
В зависимости от назначения передачи зубья могут быть прямыми, косыми, шев-
ронными, криволинейными (рисунок 1). Общий вид зубчатой передачи представлен на рисунке 2. В настоящее время эвольвентные передачи получили наибольшее рас-
пространение.

Рисунок 1 – Виды зубчатых передач
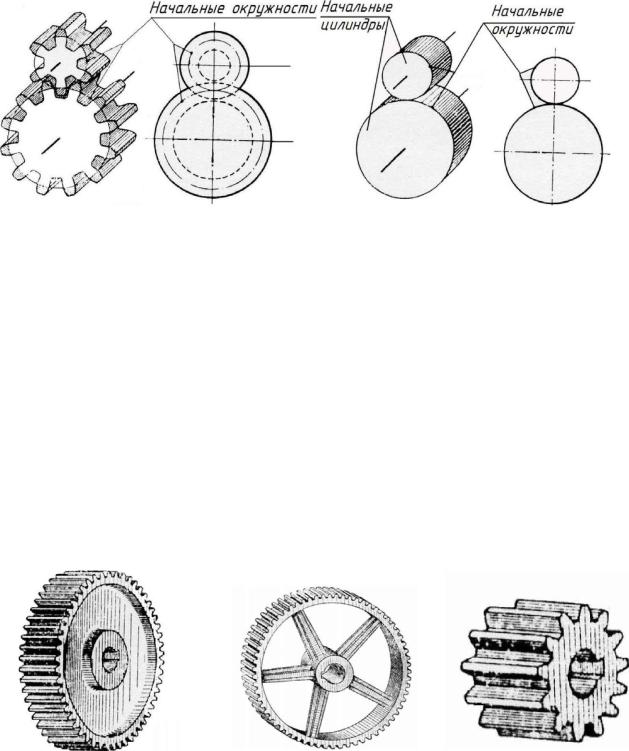
Рисунок 2 – Общий вид зубчатой передачи
1.1 Основные понятия в теории зубчатых передач
Рассматриваемые основные понятия зубчатой передачи даны в соответст-
вии с ГОСТ 6530 и представлены глоссарии электронного курса в категории
«Зубчатые передачи».
1.2 Элементы зубчатого колеса
Наиболее часто в различных машинах применяют зубчатые колёса средне-
го диаметра (примерно от 80 до 200 мм). Такие колёса изготавливают дисковы-
ми (рисунок 3а). Колёса большего диаметра делают со спицами (рисунок 3б), а
небольшого – сплошным, т.е. без диска и без спиц (рисунок 3в).
а) б) в)
а - дисковое зубчатое колесо; б - зубчатое колесо со спицами; в - сплошное зубчатое колесо
Рисунок 3 – Виды зубчатых колес Основными элементами зубчатого колеса (рисунок 4) являются зубья, ка-
ждый зуб состоит из головки зуба и ножки.
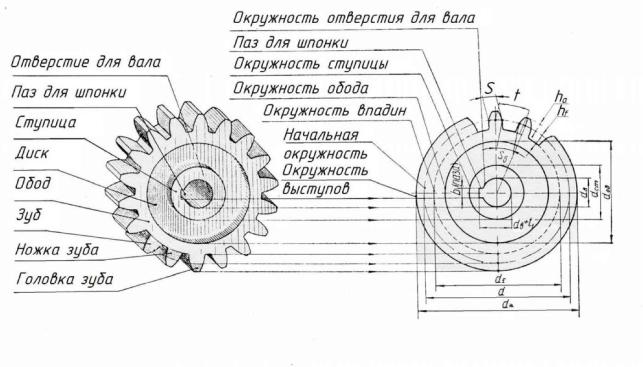
Рисунок 4 – Условные изображения элементов зубчатого колеса Зубья находятся на ободе колеса и вместе с ободом составляют зубчатый
венец, более тонкая часть колеса - диск соединяет ступицу с ободом, внутри ступицы делают отверстие для вала с пазом для шпонки. Шлицевое соедине-
ние представлено на рисунке 4 показаны условные изображения элементов зуб-
чатого колеса.
Основным геометрическим параметром, определяющим все элементы пе-
редачи, является модуль m, который выбирается в зависимости от передаваемой нагрузки из нормального ряда модулей по ГОСТ 9563.
Зубчатые колеса с модулем от 0,05 мм до 1 мм принято называть мелкомо-
дульными; от 1 до 10 мм – среднемодульными и свыше 10 мм − крупномодуль-
ными.
Мелкомодульные передачи (m 1) используются при малых нагрузках (в
приборостроении, при ручном приводе). Чем больше передаваемая нагрузка,
тем больше должен быть модуль и ширина зубчатого венца В. Рекомендуется принимать В = (3…15) m.
Число зубьев колес принято обозначать буквой Z а в передаче для ведуще-
го (шестерни) и ведомого колес - Z1 и Z2 соответственно.

В зубчатой передаче число оборотов зависит от числа зубьев колеса.
Передаточное число i = n1 = z2 , где n1 и n2 число оборотов в минуту ве- n2 z1
дущего и ведомого колеса.
Межосевое расстояние (делительное) в передаче a = m(Z1+Z2)/2.
К основным параметрам зубчатого колеса 1относятся:
da – окружность вершин – это самая большая окружность, ограничиваю-
щая вершины головок зубьев колес: её условно изображают сплошной основ-
ной линией.
d – делительная окружность (диаметр делительной окружности), деля-
щая каждый зуб на две неравные части: меньшую – головку зуба и большую – ножку зуба: её условно изображают штрихпунктирной тонкой линией.
df – окружность впадин, - окружность впадин, проходящая по очертаниям впадин между зубьями: её условно изображают сплошной тонкой линией.
dоб – окружность обода, обозначающая внутреннее очертание обода. dст – окружность ступицы, обозначающая внешнее очертание ступицы. dВ – диаметр окружности отверстия для вала.
h – высота зуба.
ha – высота головки зуба. hf – высота ножки зуба.
Pn – нормальный шаг зубьев – кратчайшее расстояние по делительной или начальной поверхности зубчатого колеса между эквидистантными од-
ноименными теоретическими линиями соседних зубьев.
S – толщина зуба по делительной окружности S = pt /2 = π m/2 на высоте головки зуба ha; толщина зуба по постоянной хорде Sc=1,387 m, измеренная на высоте hc=0,7476 m от вершины зуба. Этот показатель не зависит от числа зубьев колеса, а зависит только от модуля;
Z – число зубьев.
1 Основные формулы расчета каждого из показателей приведены в методическом указании к выполнению задания, выложенному в электронном курсе в модуле 6 «Нормирование точности зубчатых передач и колес»
m – нормальный модуль зубьев – это линейная величина в π раз мень-
шая нормального шага зубьев. Модуль – это число, которое показывает сколько миллиметров диаметра делительной окружности приходится на один зуб зубчатого колеса.
bпаза – ширина шпоночного паза. tj – глубина шпоночного паза.
Длина общей нормали это расстояние между двумя параллельными плоскостями, касательными к двум разноименным, активным боковым поверх-
ностям зубьев колеса. Номинальное значение длины общей нормали определя-
ется по формуле:
W=pt (Zw−1) +S,
где Zw= 0,111 z + 0,5 или Zw= z/9+1 – число охватываемых при измерении зубьев, которое необходимо округлять до ближайшего целого числа (см.
таблицу 1). Для колес с углом зацепления формула принимает вид:
W=m [1,476 (2Zw - 1) +0,014 Z].
Длина общей нормали прямо пропорциональна модулю, поэтому в табли-
цах справочников указывается значение длины общей нормали для m=1 (см.
таблицу 1). При изменении модуля табличное значение необходимо умножить на величину модуля.
Средняя длина общей нормали определяется по результатам измерения всех длин у колеса от зуба к зубу, как среднее арифметическое значение:
|
z |
|
|
|
|
Wi |
|
W1 W2 ... Wz |
. |
Wm |
1 |
|
||
z |
|
|||
|
|
z |
||
Ввиду погрешностей обработки, у одного зубчатого колеса длина общей нормали изменяется от зуба к зубу.
Для размещения смазки и исключения заклинивания требуется увеличи-
вать или уменьшать толщину зуба. Теоретическое зацепление считается двух-
профильным, когда контакт идет по обеим сторонам зуба.
Реальная передача имеет однопрофильное зацепление, т.е. по рабочим профилям контакт, а по нерабочим зазор.

Таблица 1– Геометрические параметры зубчатого колеса при m = 1, α= 20 °С
Число |
Количе- |
Длина |
Диаметр |
|
|
Количе- |
Длина |
Диаметр |
зубьев |
ство охва- |
общей |
основной |
|
Число |
ство охва- |
общей |
основной |
Z |
тываемых |
норма- |
окружно- |
|
зубьевZ |
тываемых |
норма- |
окруж- |
коле- |
зубьев |
ли |
сти |
|
колеса |
зубьев |
ли |
ности |
са |
Zw |
W, мм |
db, мм |
|
|
Zw |
W, мм |
db, мм |
12 |
|
4,596 |
11,276 |
|
51 |
|
16951 |
47,924 |
|
|
|
|
|
|
|
|
|
15 |
|
4,938 |
14,095 |
|
52 |
6 |
16,965 |
48,864 |
|
|
|
|
|
|
|
|
|
16 |
2 |
4,652 |
15,035 |
|
53 |
16,978 |
49,804 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
17 |
|
4,666 |
15,975 |
|
54 |
|
16,992 |
50,743 |
|
|
|
|
|
|
|
|
|
18 |
|
4,680 |
16,914 |
|
55 |
|
19,959 |
51,683 |
|
|
|
|
|
|
|
|
|
20 |
|
7,660 |
18,794 |
|
56 |
|
19,973 |
52,623 |
|
|
|
|
|
|
|
|
|
22 |
|
7,688 |
20,673 |
|
57 |
|
19,987 |
53,562 |
23 |
|
7,702 |
21,613 |
|
58 |
7 |
20,001 |
54,502 |
|
|
|
|
|
|
|
|
|
24 |
3 |
7,716 |
22,557 |
|
59 |
|
20,015 |
55,442 |
|
|
|
|
|
|
|
|
|
25 |
|
7,730 |
23,492 |
|
60 |
|
20,029 |
56,382 |
|
|
|
|
|
|
|
|
|
26 |
|
7,744 |
24,432 |
|
62 |
|
20,057 |
58,261 |
|
|
|
|
|
|
|
|
|
27 |
|
7,758 |
25372 |
|
65 |
|
23,051 |
61,08 |
|
|
|
|
|
|
|
|
|
28 |
|
10,725 |
26,311 |
|
66 |
|
23,065 |
62,02 |
|
|
|
|
|
|
8 |
|
|
29 |
|
10,739 |
27,251 |
|
68 |
23,093 |
63,899 |
|
|
|
|
|
|
|
|
|
|
30 |
|
10,753 |
28,191 |
|
70 |
|
23,121 |
66,778 |
31 |
|
10,767 |
29,13 |
|
72 |
|
23,149 |
67,578 |
|
4 |
|
|
|
|
|
|
|
32 |
10,781 |
30,07 |
|
75 |
|
26,051 |
70,477 |
|
|
|
|
|
|
|
|
|
|
33 |
|
10,795 |
31,001 |
|
76 |
|
26,157 |
71,416 |
|
|
|
|
|
|
9 |
|
|
34 |
|
10,809 |
31,95 |
|
78 |
26,185 |
73,296 |
|
|
|
|
|
|
|
|
|
|
35 |
|
10,872 |
32,889 |
|
79 |
|
26,199 |
74,236 |
|
|
|
|
|
|
|
|
|
36 |
|
10,836 |
33,829 |
|
80 |
|
26,213 |
75,175 |
|
|
|
|
|
|
|
|
|
37 |
|
13,803 |
34,769 |
|
82 |
|
29,194 |
77,055 |
|
|
|
|
|
|
10 |
|
|
38 |
|
13,817 |
35,708 |
|
85 |
29,236 |
79,874 |
|
|
|
|
|
|
|
|
|
|
39 |
|
13,831 |
36,648 |
|
90 |
|
29,306 |
84,572 |
|
|
|
|
|
|
|
|
|
40 |
|
13,845 |
37,588 |
|
92 |
|
32,286 |
86,452 |
|
5 |
|
|
|
|
|
|
|
41 |
13,859 |
38,527 |
|
94 |
|
32,314 |
88,331 |
|
|
|
|
|
|
|
11 |
|
|
42 |
|
13,873 |
39.467 |
|
95 |
32,328 |
89,271 |
|
|
|
|
|
|
|
|
|
|
43 |
|
13,887 |
40,407 |
|
98 |
|
32,369 |
92,09 |
|
|
|
|
|
|
|
|
|
44 |
|
13,900 |
41,346 |
|
100 |
|
32,398 |
93,97 |
|
|
|
|
|
|
|
|
|
45 |
|
13,914 |
42,286 |
|
100 |
12 |
35,350 |
93,97 |
|
|
|
|
|
|
|
|
|
46 |
|
16,881 |
43,226 |
|
105 |
35,420 |
98,668 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
47 |
|
16,895 |
44,166 |
|
108 |
|
38,414 |
101,468 |
|
6 |
|
|
|
|
|
|
|
48 |
16,909 |
45,105 |
|
110 |
13 |
38,442 |
103,336 |
|
|
|
|
|
|
|
|
|
|
49 |
|
16,923 |
46,045 |
|
122 |
38,47 |
105,246 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
50 |
|
16,937 |
46,985 |
|
115 |
|
38,512 |
108,066 |
|
|
|
|
|
|
|
|
|
Величина бокового зазора зависит от условий эксплуатации: температуры,
смазки, нагрузки, условий загрязнения и других требований (см. пункты «Сте-
пени точности и виды сопряжения» и «Выбор степени точности зубчатой пере-
дачи»).
У зубчатого колеса различают окружной шаг по делительной окружности: pt=360/Z= m,
и шаг зацепления или основной шаг (шаг по основной окружности): pb=pt cos = m cos .
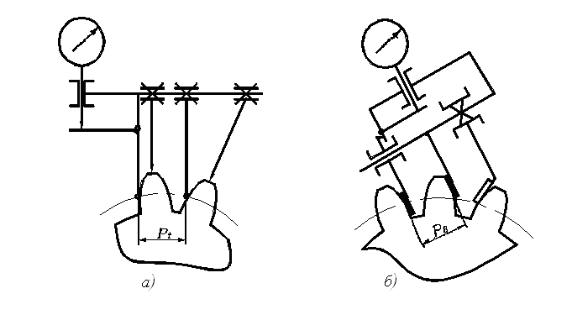
Рисунок 5 – Схема измерения шаговых параметров зубчатого колеса:
a - окружного шага; б - шага зацепления
Контроль окружного шага может быть выполнен накладным шагомером или универсальным зубоизмерительным прибором. Базирующие наконечники опираются на наружный (или внутренний) диаметр (рисунок 5, а). Широко ис-
пользуется метод измерения от «первого шага», принятого за номинальное зна-
чение с определением отклонений от него. Измерив по всей окружности Z раз,
можно построить график и определить накопленную погрешность окружного шага.
Шаг зацепления (основной шаг) контролируется в плоскости, касательной к основному цилиндру (рисунок 5, б). Настройка прибора производиться на
ноль по блоку кольцевых мер длины, равному номинальному значению шага зацепления. Метод измерения относительный, так как прибор показывает по-
грешность шага зацепления:
рb = рbr – рb ном.
2 Допуски цилиндрических зубчатых передач
Точность изготовления зубчатых передач и червячных колес задается сте-
пенью по нормам кинематической точности, плавности работы и контакта зубь-
ев в передаче, а требования к боковому зазору – видом сопряжений и видом до-
пуска бокового зазора. К нормам точности относятся допуски и отклонения, ог-
раничивающие отдельные виды погрешностей.
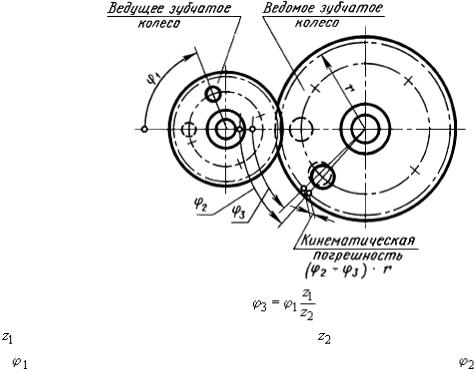
1 Кинематическая погрешность передачи – разность между действи-
тельным и номинальным (расчетным) углами поворота ведомого зубчатого ко-
леса передачи. Выражается в линейных величинах длиной дуги его делитель-
ной окружности (Рисунок 6).
,
где |
– число зубьев ведущего зубчатого колеса; |
- число зубьев ведомого зубчатого ко- |
|
леса; |
- действительный угол поворота ведущего зубчатого колеса; |
- действительный |
|
угол поворота ведомого зубчатого колеса; 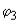 - номинальный угол поворота ведомого зубчатого колеса
- номинальный угол поворота ведомого зубчатого колеса
Рисунок 6
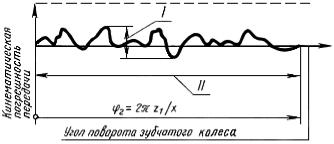
1.1 Наибольшая кинематическая погрешность передачи 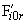 – наибольшая алгебраическая разность значений кинематической погрешности передачи за полный цикл изменения относительного положения зубчатых колес (т.е. в пре-
– наибольшая алгебраическая разность значений кинематической погрешности передачи за полный цикл изменения относительного положения зубчатых колес (т.е. в пре-
делах числа оборотов большего зубчатого колеса, равного частному от деления числа зубьев меньшего зубчатого колеса на общий наибольший делитель чисел зубьев обоих зубчатых колес передачи) (Рисунок 7).
 - угол поворота большего колеса;
- угол поворота большего колеса; 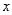 - общий наибольший делитель чисел зубьев
- общий наибольший делитель чисел зубьев  и
и  соответственно шестерни и колеса; I - наибольшая кинематическая погрешность передачи
соответственно шестерни и колеса; I - наибольшая кинематическая погрешность передачи 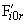 ; II - полный цикл изменения относительного положения зубчатых колес
; II - полный цикл изменения относительного положения зубчатых колес
Рисунок 7
1.2 Допуск на кинематическую погрешность передачи 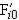
2 Кинематическая погрешность зубчатого колеса – разность между действительным и номинальным (расчетным) углами поворота зубчатого коле-
са на его рабочей оси, ведомого измерительным зубчатым колесом при номи-
нальном взаимном положении осей вращения этих колес. Выражается в линей-
ных величинах длиной дуги делительной окружности.
Примечания: 1 Под рабочей осью зубчатого колеса понимается ось, вокруг которой оно вращается в передаче.
2 Под измерительным зубчатым колесом понимается зубчатое колесо повышенной точности, применяемое в качестве измерительного элемента для однопрофильного и двух-
профильного методов контроля зубчатых колес.
2.1 Наибольшая кинематическая погрешность зубчатого колеса 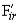 – наи-
– наи-
большая алгебраическая разность значений кинематической погрешности зуб-
чатого колеса в пределах его полного оборота (Рисунок 8).
