
Вариант 13.
-
Имеется выборка из нормальной совокупности с известным параметром
 и неизвестным параметром
и неизвестным параметром
 .
Построить наиболее мощный критерий
уровня
.
Построить наиболее мощный критерий
уровня
 для проверки гипотезы
для проверки гипотезы
 ,
против альтернативы:
,
против альтернативы:
 .
Используя построенный критерий, по
выборочным данным нормальной случайной
величины
.
Используя построенный критерий, по
выборочным данным нормальной случайной
величины
 (таблица 1), на уровне значимости
(таблица 1), на уровне значимости
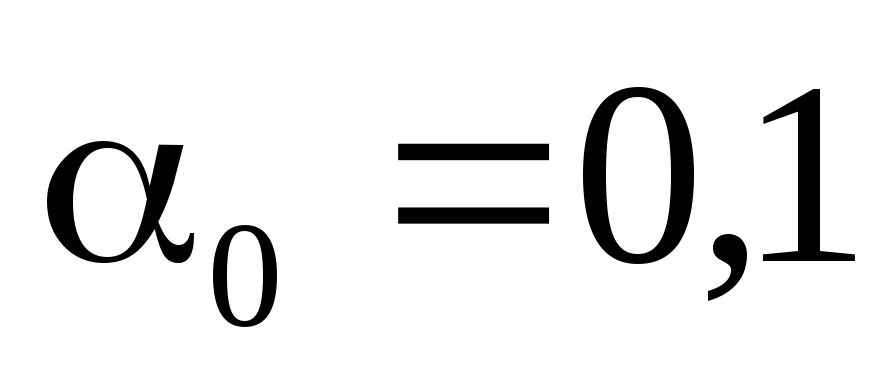 проверить гипотезу
проверить гипотезу
 ,
если
,
если
 .
Указать мощность критерия, если
.
Указать мощность критерия, если
 .
. -
Имеется выборка из нормальной совокупности с неизвестными параметрами
 и
и
 .
Построить минимаксный критерий для
проверки гипотезы
.
Построить минимаксный критерий для
проверки гипотезы
 ,
против альтернативы:
,
против альтернативы:
 .
Используя построенный критерий, по
выборочным данным нормальной случайной
величины
.
Используя построенный критерий, по
выборочным данным нормальной случайной
величины
 (таблица 1), принять одну из двух гипотез:
(таблица 1), принять одну из двух гипотез:
 ,
,
 .
Указать уровень значимости и мощность
критерия.
.
Указать уровень значимости и мощность
критерия. -
Даны две выборки объемов
 и
и
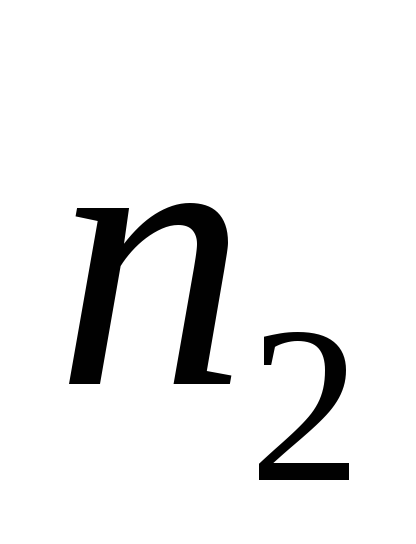 из генеральных совокупностей, имеющих
нормальное распределение с математическими
ожиданиями
из генеральных совокупностей, имеющих
нормальное распределение с математическими
ожиданиями
 и
и
 и дисперсиями
и дисперсиями
 и
и
 соответственно (все параметры неизвестны).
Построить асимптотический критерий
отношения правдоподобия уровня
соответственно (все параметры неизвестны).
Построить асимптотический критерий
отношения правдоподобия уровня
 для проверки гипотезы
для проверки гипотезы
 против альтернативы
против альтернативы
 .
. -
По критерию Пирсона при уровне значимости
 проверить гипотезу о распределении
случайной величины
проверить гипотезу о распределении
случайной величины
 по закону Лапласа с плотностью
по закону Лапласа с плотностью
 ,
,
 ,
где параметры
,
где параметры
 и
и
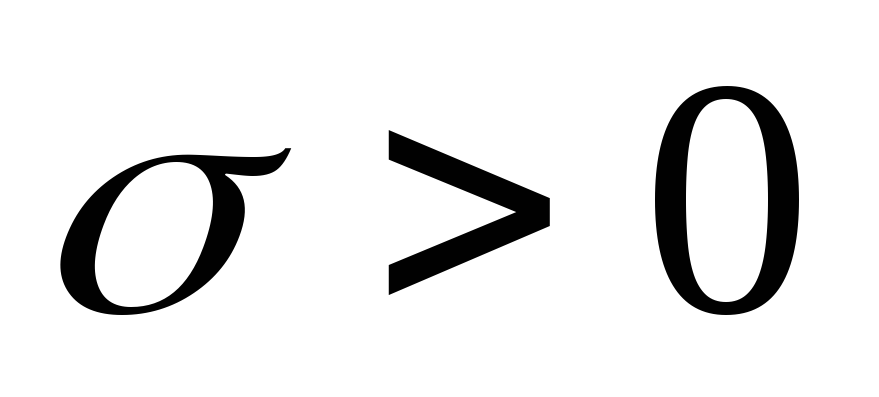 - неизвестны, если задано
- неизвестны, если задано
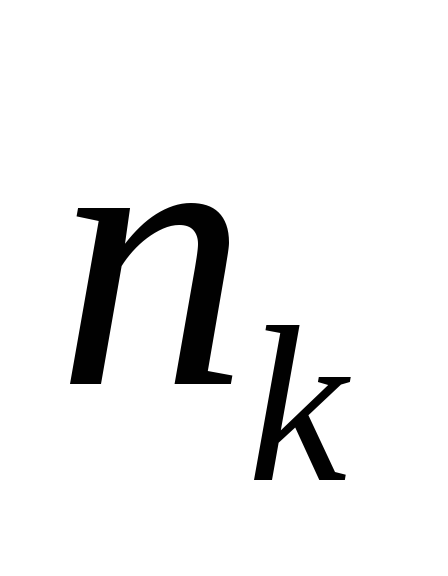 попаданий выборочных значений случайной
величины
попаданий выборочных значений случайной
величины
 в подинтервал
в подинтервал
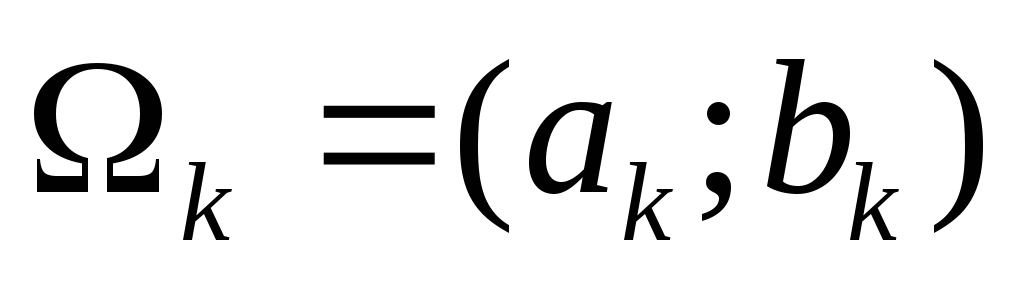 .
Указать достигнутый уровень значимости.
Указать достигнутый уровень значимости.
.
Указать достигнутый уровень значимости.
Указать достигнутый уровень значимости.
-
Интервал
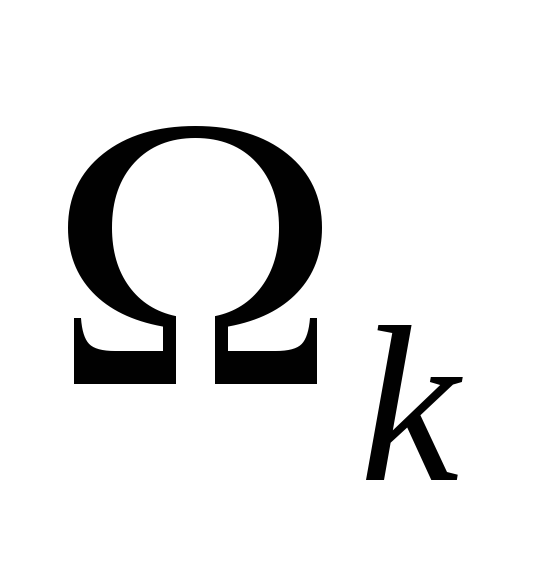
(-2; 3)
(3; 5)
(5; 7)
(7; 9)
(9; 11)
(11; 13)
(13; 18)
Частота

5
12
23
35
18
6
1
-
Используя критерий Жарке-Бера, при уровне значимости
 ,
на основе выборочных данных случайной
величины
,
на основе выборочных данных случайной
величины
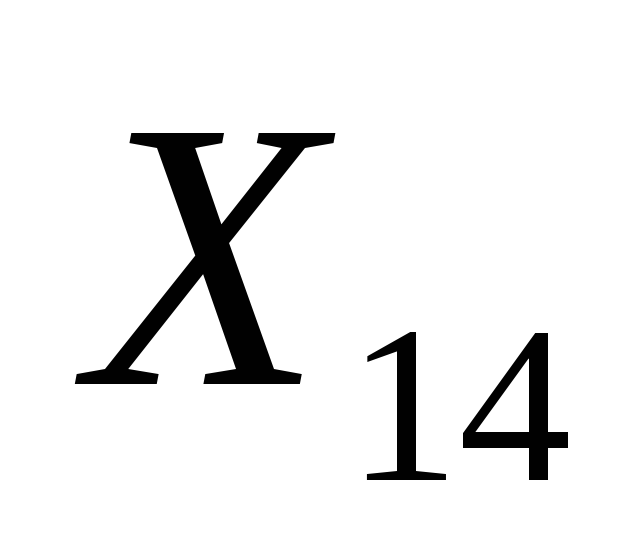 (таблица 1), проверить гипотезу о
распределении
(таблица 1), проверить гипотезу о
распределении
 по нормальному закону. Указать достигнутый
уровень значимости.
по нормальному закону. Указать достигнутый
уровень значимости. -
По двум независимым выборкам объемов
 и
и
 нормально распределенных величин
нормально распределенных величин
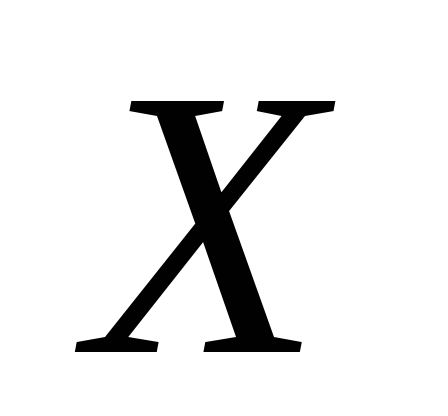 и
и
 найдены выборочные средние
найдены выборочные средние
 ,
,
 .
Дисперсии величин
.
Дисперсии величин
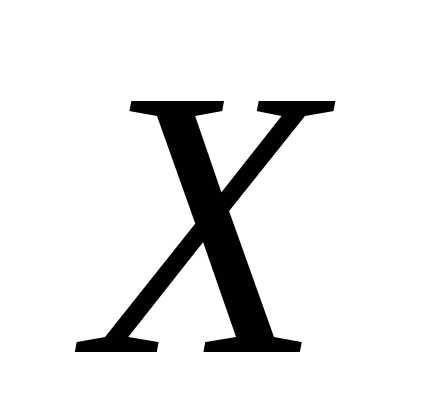 и
и
 известны
известны
 ,
,
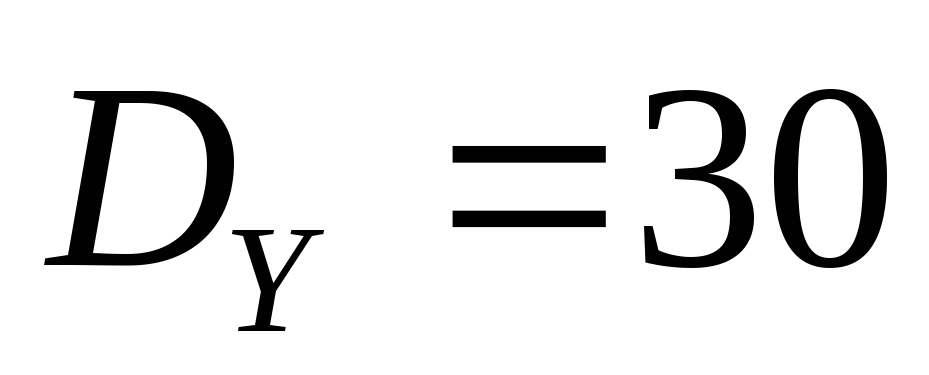 .
При уровне значимости
.
При уровне значимости
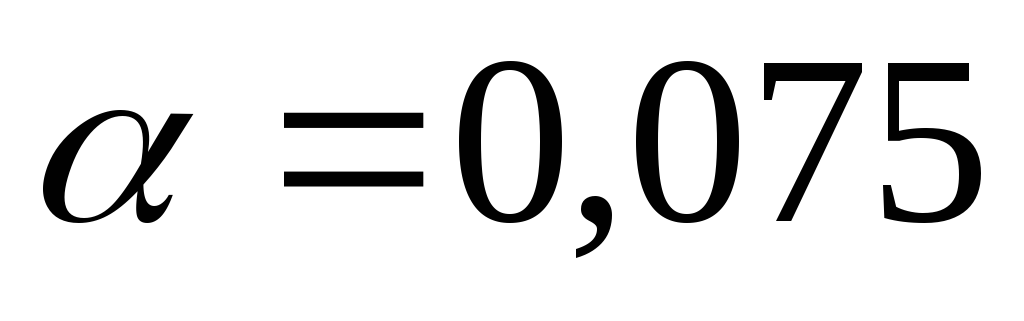 проверить гипотезу
проверить гипотезу
 ,
при конкурирующей
,
при конкурирующей
 .
.
Вариант 14.
-
Имеется выборка из нормальной совокупности с известным параметром
 и неизвестным параметром
и неизвестным параметром
 .
Построить наиболее мощный критерий
уровня
.
Построить наиболее мощный критерий
уровня
 для проверки гипотезы
для проверки гипотезы
 ,
против альтернативы:
,
против альтернативы:
 .
Используя построенный критерий, по
выборочным данным нормальной случайной
величины
.
Используя построенный критерий, по
выборочным данным нормальной случайной
величины
 (таблица 1), на уровне значимости
(таблица 1), на уровне значимости
 проверить гипотезу
проверить гипотезу
 ,
если
,
если
 .
Указать мощность критерия, если
.
Указать мощность критерия, если
 .
. -
Имеется выборка из нормальной совокупности с неизвестным параметром
 и известным параметром
и известным параметром
 .
Построить минимаксный критерий для
проверки гипотезы
.
Построить минимаксный критерий для
проверки гипотезы
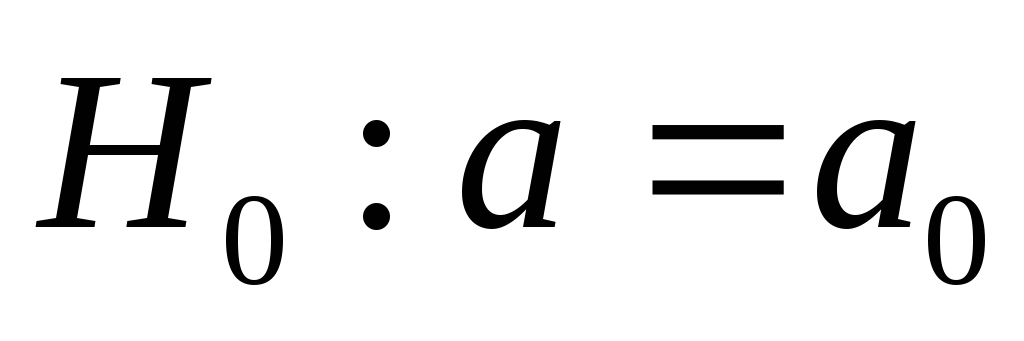 ,
против альтернативы:
,
против альтернативы:
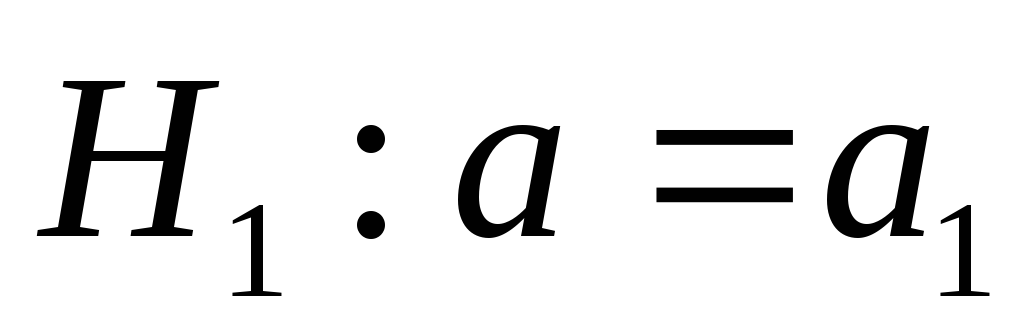 .
Используя построенный критерий, по
выборочным данным нормальной случайной
величины
.
Используя построенный критерий, по
выборочным данным нормальной случайной
величины
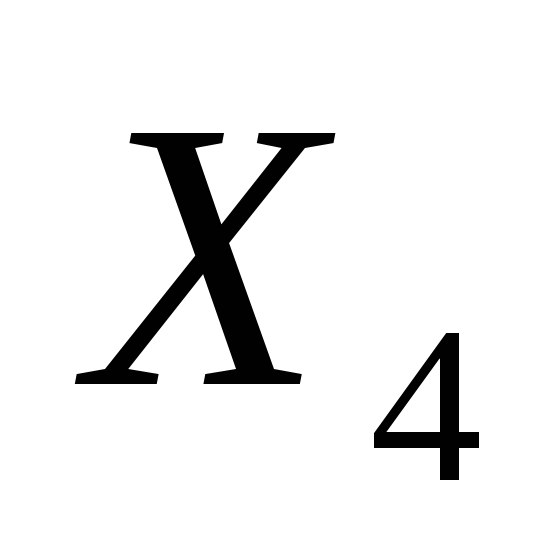 (таблица 1), принять одну из двух гипотез:
(таблица 1), принять одну из двух гипотез:
 ,
,
 ,
если
,
если
 .
. -
Дана выборка
 из генеральной совокупности, имеющей
плотность распределения
из генеральной совокупности, имеющей
плотность распределения
 ,
с неизвестным параметром
,
с неизвестным параметром
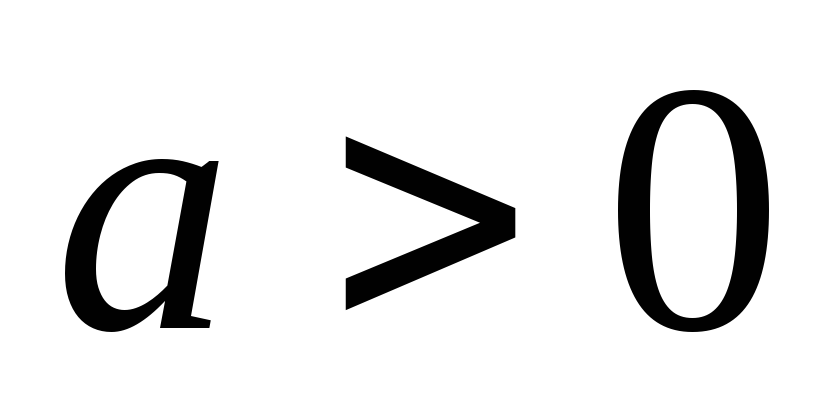 .
Построить асимптотический критерий
отношения правдоподобия уровня
.
Построить асимптотический критерий
отношения правдоподобия уровня
 для проверки гипотезы
для проверки гипотезы
 против альтернативы
против альтернативы
 .
. -
По критерию Пирсона при уровне значимости
 проверить гипотезу о распределении
случайной величины
проверить гипотезу о распределении
случайной величины
 по закону с плотностью
по закону с плотностью
 ,
,
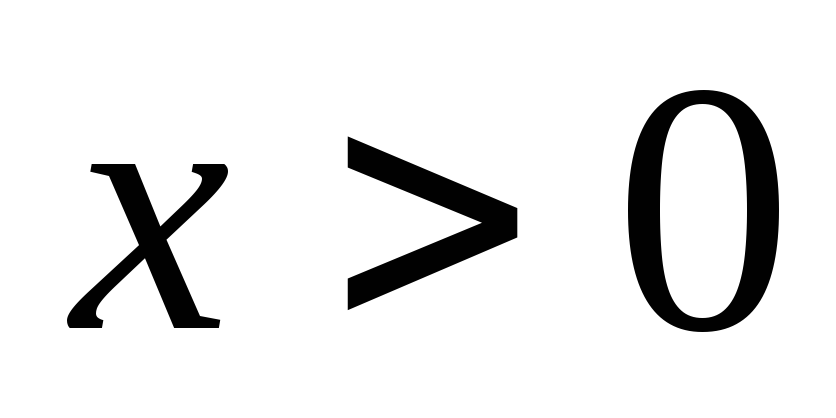 ,
где параметр
,
где параметр
 - неизвестен, если задано
- неизвестен, если задано
 попаданий выборочных значений случайной
величины
попаданий выборочных значений случайной
величины
 в подинтервал
в подинтервал
 .
Указать достигнутый уровень значимости.
.
Указать достигнутый уровень значимости.
-
Интервал

(0; 1)
(1; 2)
(2; 3)
(3; 4)
(4; 5)
(5; 6)
(6; 10)
Частота
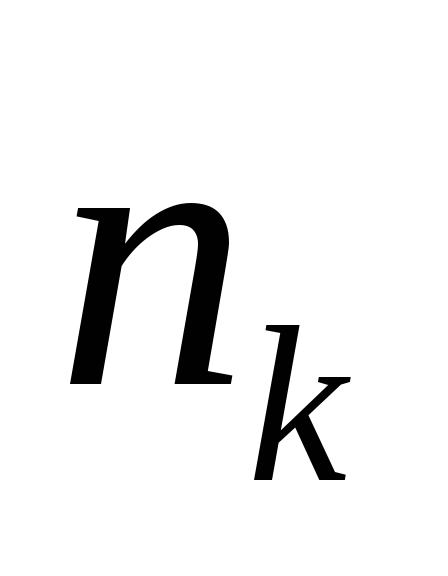
10
25
23
14
13
7
8
-
Используя критерий Жарке-Бера, при уровне значимости
 ,
на основе выборочных данных случайной
величины
,
на основе выборочных данных случайной
величины
 (таблица 1), проверить гипотезу о
распределении
(таблица 1), проверить гипотезу о
распределении
 по нормальному закону.
по нормальному закону. -
По двум независимым выборкам объемов
 и
и
 нормально распределенных величин
нормально распределенных величин
 и
и
 найдены выборочные средние
найдены выборочные средние
 ,
,
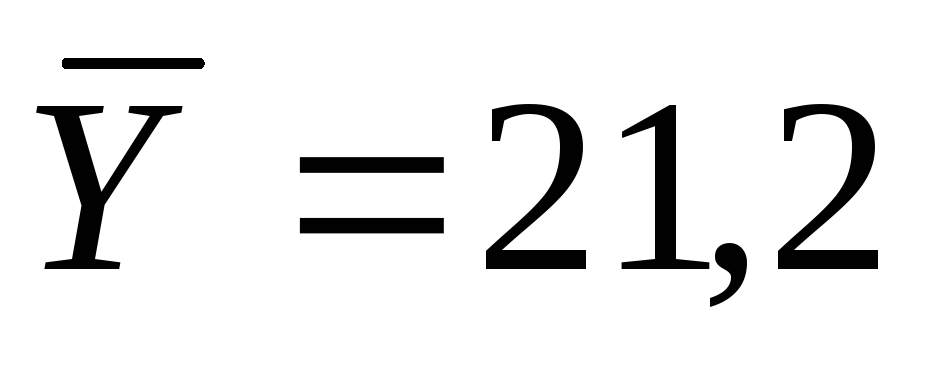 и исправленные выборочные дисперсии
и исправленные выборочные дисперсии
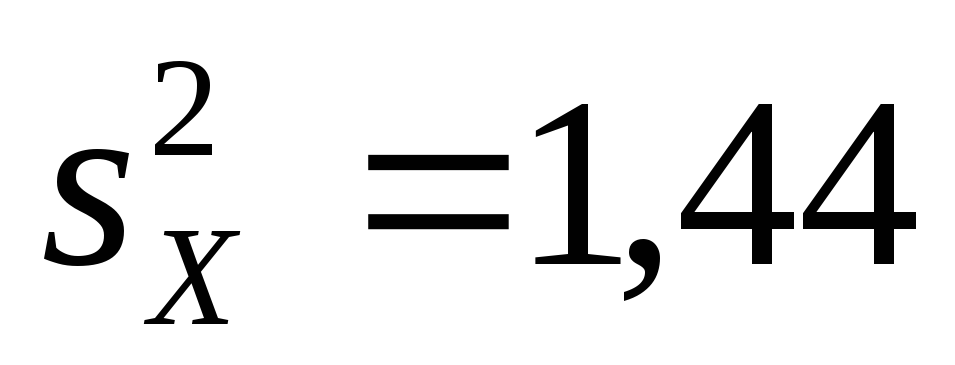 ,
,
 .
При уровне значимости
.
При уровне значимости
 проверить гипотезу
проверить гипотезу
 ,
при конкурирующей
,
при конкурирующей
 .
.
