
- •Высшая математика теория вероятностей и метематическая статистика
- •Варианты заданий
- •Контрольная работа №4
- •Примеры решения задач
- •Найти: 1) математическое ожидание ; 2) дисперсию ; 3) среднее квадратическое отклонение .
- •Где в первой строке даны значения случайной величины х, а во второй – вероятности этих значений, то математическое ожидание вычисляется по формуле
- •Теория вероятностей справочные формулы
- •Вопросы и задачи для зачета по контрольной работе №4 Случайные события
- •Случайные величины и их числовые характеристики
- •Случайные события
- •Случайная величина и ее числовые характеристики
- •Контрольная работа №5
- •Методические советы по выполнению задания
- •Приложения
Теория вероятностей справочные формулы
СОБЫТИЯ А, В, С…
|
Сумма событий (хотя бы или А, илиВ) |
А + В |
|
|
Произведение событий (и А, иВодновременно) |
А В |
|
|
Виды событий |
Обозначение или определение | |
|
Невозможное |
V– заведомо не произойдет | |
|
Достоверное (истинное) |
U– обязательно произойдет | |
|
Случайное |
в результате испытания может либо произойти, либо не произойти | |
|
Несовместные АиВ |
если появление Аисключает появлениеВ, т. е.А В= V | |
|
Совместные АиВ |
если появление Анеисключает появлениеВ, т. е.А В V | |
|
Равновозможные АиВ |
если ни одно из них не является более возможным, чем другое | |
|
Противоположные
А и |
если
| |
|
Полная группа А1,А2,…Аk |
если
| |
|
Независимые А иВ |
если А не зависит отВ и наоборот | |
СОЕДИНЕНИЯ
|
РАЗМЕЩЕНИЯ – группы элементов, отличающиеся друг от друга и элементами, и порядком |
|
|
ПЕРЕСТАНОВКИ – группы элементов, отличающиеся друг от друга только порядком элементов. |
|
|
СОЧЕТАНИЯ – группы элементов, отличающиеся друг от друга только самими элементами |
|
|
ОТНОСИТЕЛЬНАЯ
ЧАСТОТА события А п– общее число испытаний m– число появлений событияА |
ВЕРОЯТНОСТЬ события А
п– общее число всех равновозможных несовместных элементарных исходов, образующих полную группу m– число исходов, благоприятствующих событиюА | |||
|
ЗАКОН БОЛЬШИХ
ЧИСЕЛ БЕРНУЛЛИ при
| ||||
|
СВОЙСТВА ВЕРОЯТНОСТИ |
|
|
| |
|
СЛОЖЕНИЕ: Если АиВ несовместны, то
|
ПРОИЗВЕДЕНИЕ: Если АиВ независимы, то
Если
АиВзависимы, то Условной вероятностью РАназывают вероятность событияВ, вычисленную в предположении, что событиеА уже произошло. | |||
|
Следствия: 1. Если А
и 2. Вероятность
появления хотя бы одного события из
А1,А2,…Аk
: | ||||
|
ФОРМУЛА
ПОЛНОЙ ВЕРОЯТНОСТИ: Апроисходит
с одной из гипотезНi.
ЕслиН1+Н2+…+Нп=U;
HiHj=V;
ij,
то | ||||
|
ФОРМУЛА БЕЙЕСА позволяет найти изменение вероятности гипотез, если событие Апроизошло.
| ||||
ПОВТОРЕНИЕ ИСПЫТАНИЙ
|
Производится писпытаний (независимых), вероятность
каждого | |
|
ФОРМУЛА БЕРНУЛЛИ ( п– мало)
|
ЛОКАЛЬНАЯ ТЕОРЕМА ЛАПЛАСА (п– велико)
|
|
ФОРМУЛА ПУАССОНА (р– мало,п– велико )
|
ИНТЕГРАЛЬНАЯ ТЕОРЕМА ЛАПЛАСА
|
|
Вероятность появления
хотя бы одного события в писпытаниях: | |
|
Примечание:
|
|
|
х
0
а=0 =1 |
у
0,5
у=Ф(х)
0,5
|
|
Отклонение W(A)от постоянной вероятности в независимых испытаниях
| |
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
|
Случайная величины – это величина, которая в результате опыта со случайным исходом принимает то или иное значение . Х– случайная величина,х– ее возможное значение.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ДИСКРЕТНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА – это случайная величина, у которой множество возможных значений конечно или счетно (т.е. их можно перенумеровать в каком-то порядке). |
НЕПРЕРВЫНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА – это случайная величина, у которой множество возможных значений сплошь занимает какой-то участок числовой оси, границы которого могут быть как зафиксированными, так и неопределенными. | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ЗАКОН РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ – это всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующим им вероятностям (для дискретной случайной величины) или плотностями вероятностей (для непрерывной случайной величины). | |||||||||||||||||||||||||||||||||||||||||||||||||||||
р1+р2+ …+рп+…=1рп- вероятности Многоугольник распределения |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ – это вероятность того, что случайная величина примет значение меньшее, чем заданное х, т.е.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Функция распределения любой дискретной случайной величины есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины и равны вероятностям этих значений. |
Свойства: 1. F(x)– неубывающая функция 2. F()=0 3. F(+)=1 4. 0 F(x)1 5.
6.
|
Функция распределения любой непрерывной случайной величины есть непрерывная функция в любой точке и дифференцируема всюду.
Вероятность любого отдельного
значения непрерывной случайной
величины равна нулю, т.е.
Связь между плотностью и функцией
распределения непрерывной случайной
величины
| |||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
F
1
р р
х1 0 х2 х3 …хп х |
| |||||||||||||||||||||||||||||||||||||||||||||||||||
|
ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН | |||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Дискретная случайная величина
|
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ
ДИСПЕРСИЯ
СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ |
Непрерывная случайная величина
| |||||||||||||||||||||||||||||||||||||||||||||||||||
|
Свойства: М(С)=С D(С)=0 М(СХ)=СМ(Х) D(CX)=C2D(X) М(ХY)=М(Х)М(Y) D(ХY)=D(Х)+D(Y) М(ХY)=М(Х)М(Y) | |||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ВИДЫ РАСПРЕДЕЛЕНИЙ СЛУЧАЙНЫХ ВЕЛИЧИН | |||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Дискретная случайная величина
БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ М(Х)=пр; D(Х)=прq; q=1p
РАСПРЕДЕЛЕНИЕ ПУАССОНА М(Х)=; D(Х)=; =пр10; р-мало;п-велико
ГЕОМЕТРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ М(Х)=
|
Непрерывная случайная величина НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
График плотности распределения – кривая Гаусса или нормальная кривая.
Вероятность попадания в заданный интервал
Вероятность заданного отклонения
Правило
трех сигм
| ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Непрерывная случайная величина
РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ
ПОКАЗАТЕЛЬНОЕ РАСПРЕДЕЛЕНИЕ
Для нормального распределения
Интеграл Пуассона
| |||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ЗАКОН БОЛЬШИХ ЧИСЕЛ–ТЕОРЕМА ЧЕБЫШЕВА Если
Х1, Х2, …,
Хп– попарно независимые
случайные величины, причем дисперсии
их равномерно ограничены, то где >0 сколь угодно малое число. НЕРАВЕНСТВО ЧЕБЫШЕВА
| |||||||||||||||||||||||||||||||||||||||||||||||||||||



 А В
А В 





 А В
А В 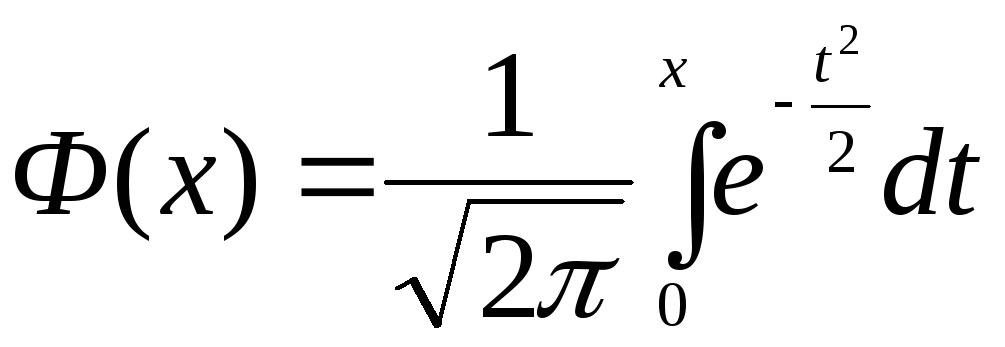 - нечетная функция, т.е.
- нечетная функция, т.е. у
у






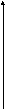



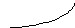 0
х
0
х






 или
или







 р1
… х
р1
… х х1
х2
хп
х1
х2
хп вероятностейХ.
вероятностейХ.
 f(x)Ее свойства:
f(x)Ее свойства:
 1.
1. График
плотности 2 .
График
плотности 2 .






 (x)
(x)
 1+р2
1+р2 1
1




 F(x)1
F(x)1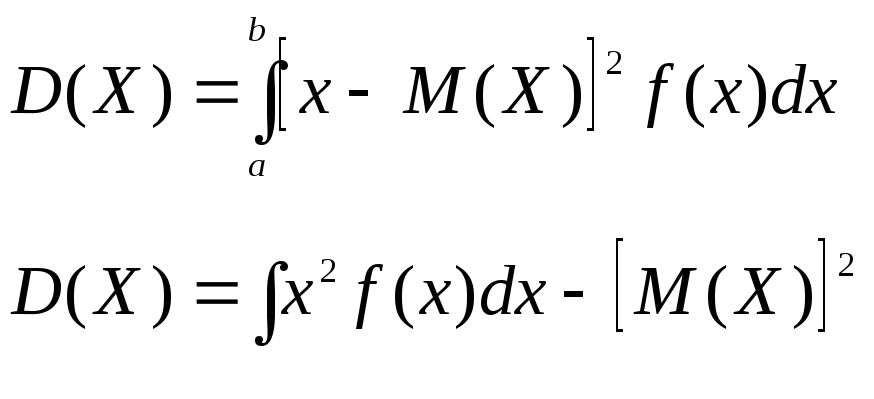
 ,
гдеа=М(Х); =(Х).
,
гдеа=М(Х); =(Х). А
А
 (x)
(x)
 В1 В2
В1 В2
 ;
; ;
; - функция Лапласа.
- функция Лапласа.