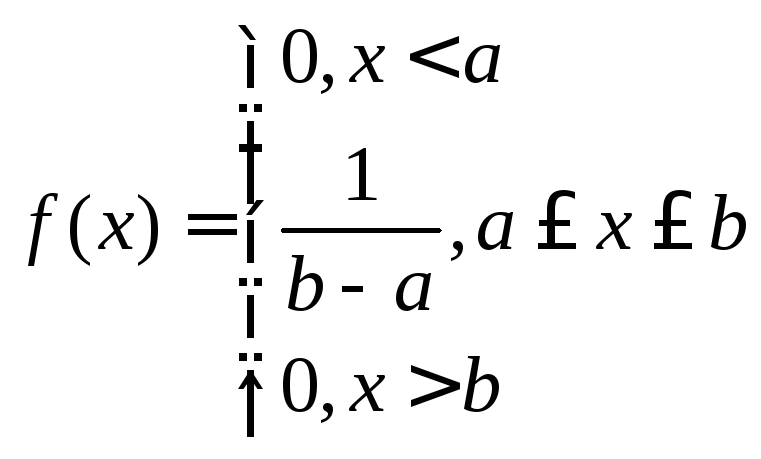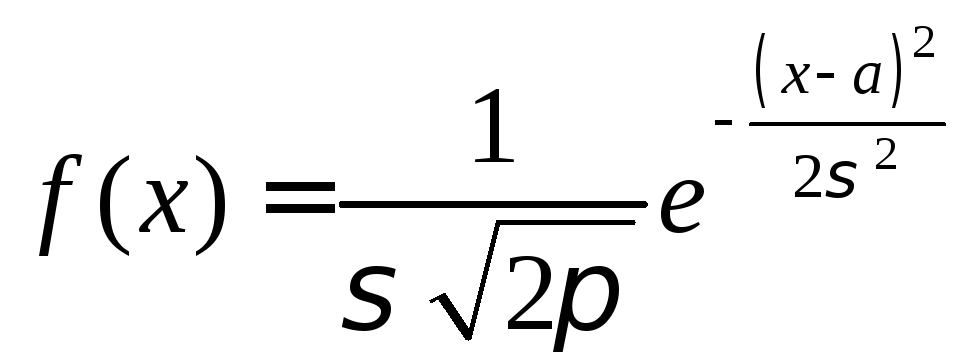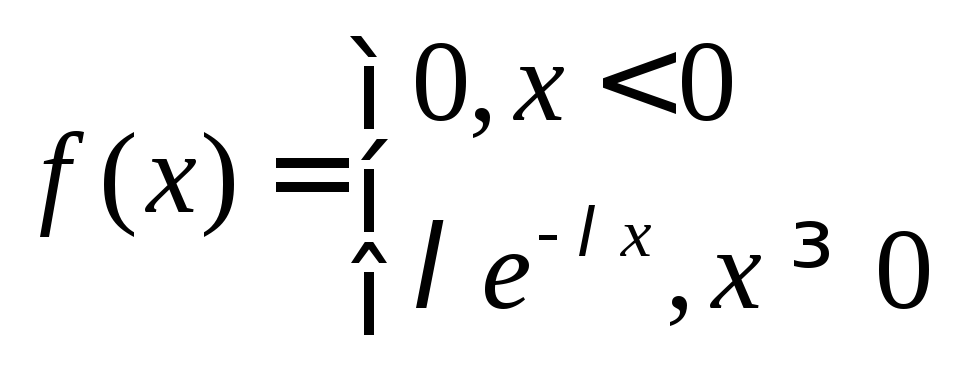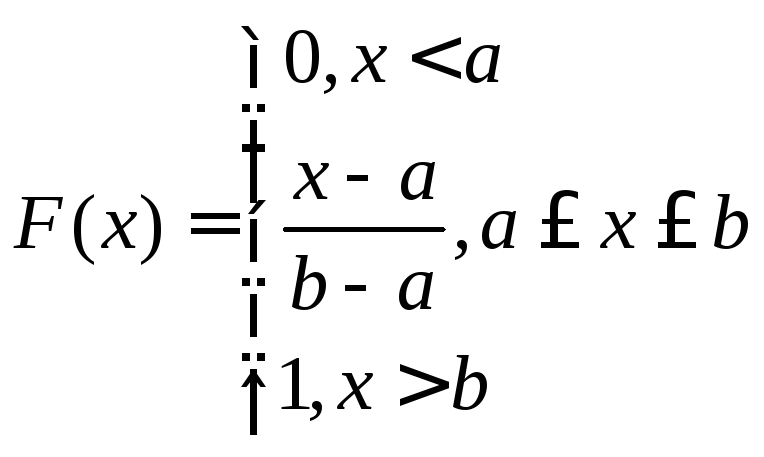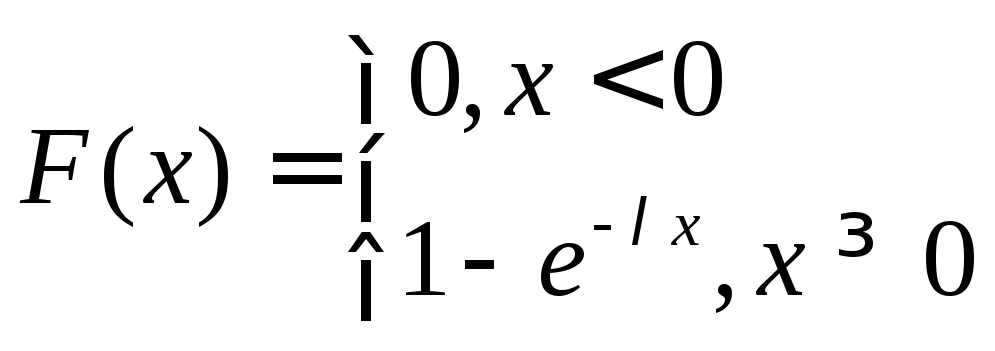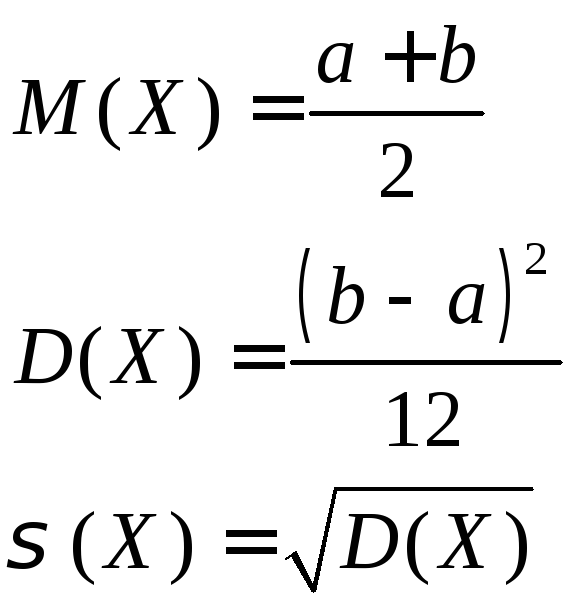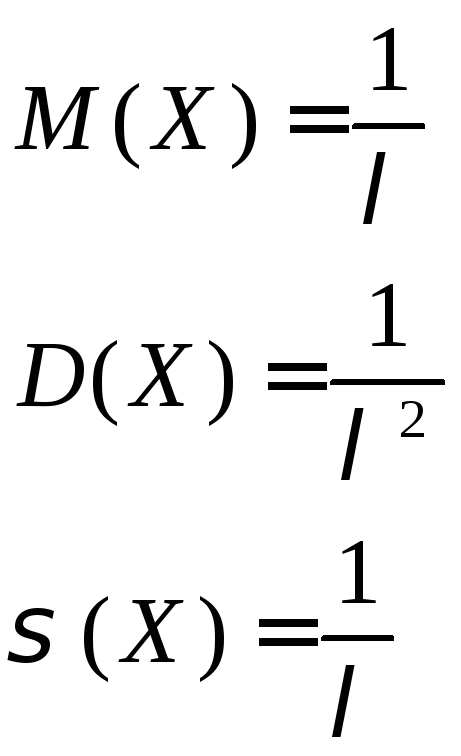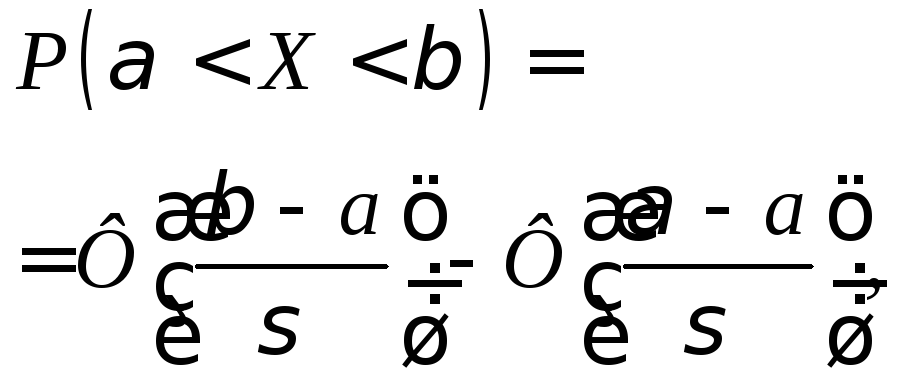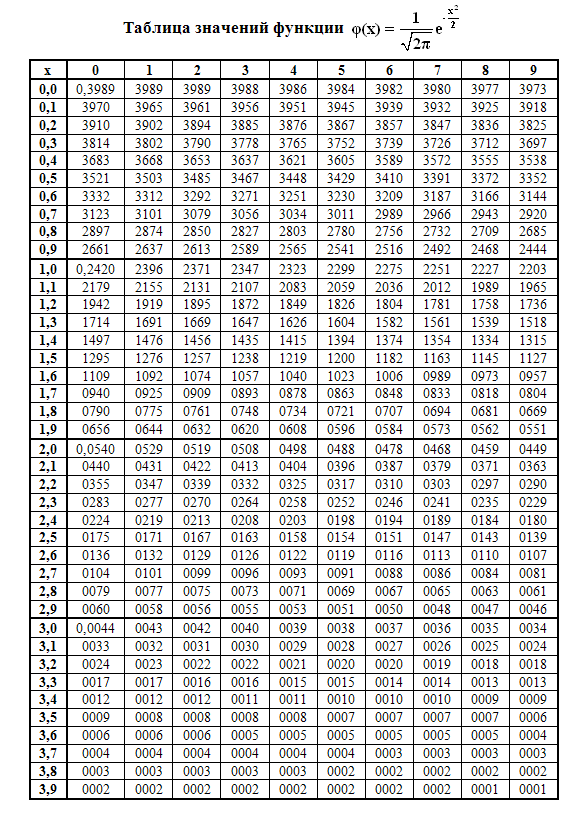
Случайные величины

Дискретная случайная величина

Опр. Дискретной случайной величиной (ДСВ) называется величина, возможные значения которой изолированы друг от друга, и их можно занумеровать.

Закон распределения ДСВ задаётся в виде таблицы:

X	x1	x2	…	xn
P	p1	p2	…	pn

x₁, x₂, …, x_n – возможные значения величины, p₁, p₂, …, p_n – их вероятности, причём

Числовые характеристики дискретной случайной величины

1) Математическое ожидание:

Вероятностный смысл: математическое ожидание величины приближённо равно её среднему значению.

Свойства М(Х):

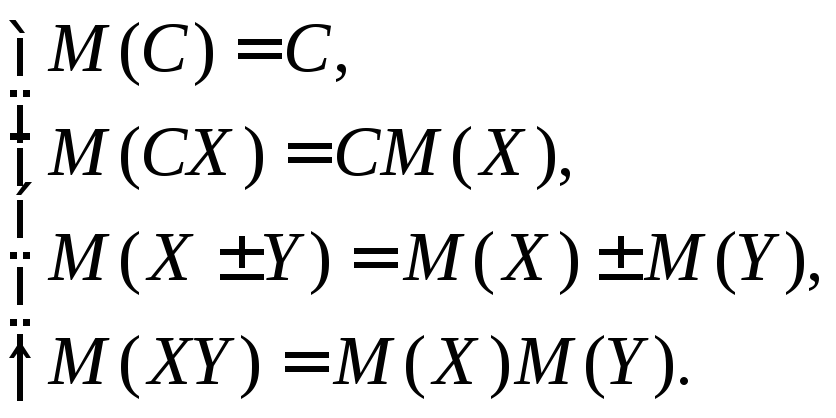
2) Дисперсия – число, характеризующее степень разброса значений величины вокруг её среднего значения.

или

Свойства D(X):

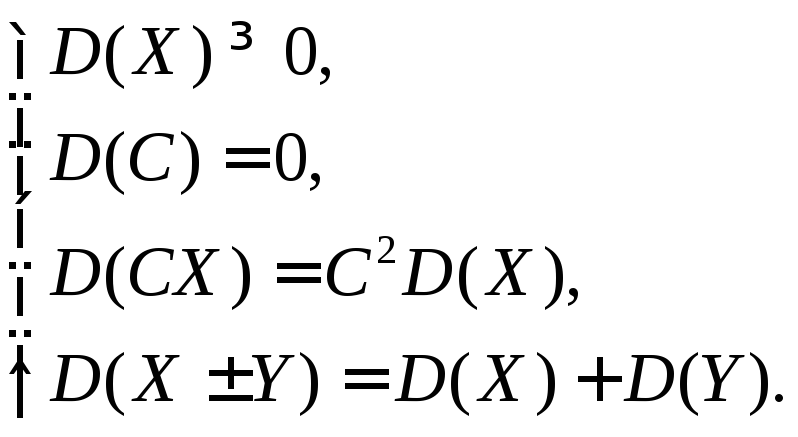
3) Среднее квадратическое отклонение:

4) Мода (Мо) – наиболее вероятное значение.

5) Медиана (Ме) – значение, делящее распределение на две равные части.

Виды распределения ДСВ

Вид	Случайная величина Х	Формула	Числовые характеристики
Биноми-альное	Х – число наступлений события А в n повторных независимых испытаниях.
Пуассона	Х – число наступлений события А в n повторных независимых испытаниях, причём n - велико (n≥100), p – мало (p≤0,1).	, где
Геометри-ческое	Х – число испытаний, проведённых до первого появления события А.	Если число испытаний ограничено, то	По общим формулам

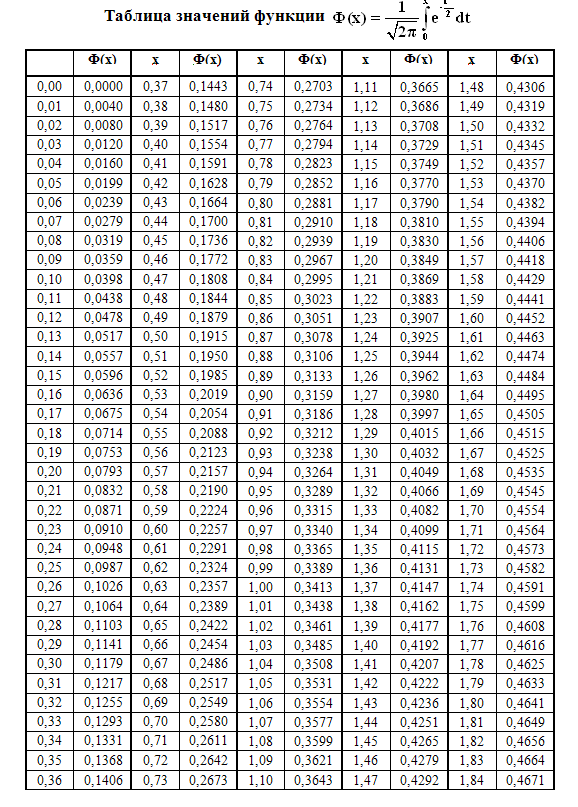
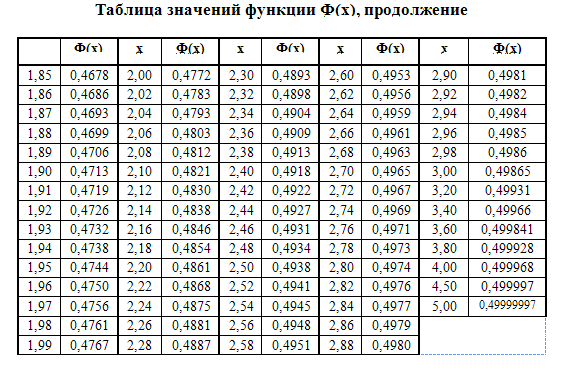
Непрерывная случайная величина

Опр. Непрерывной случайной величиной (НСВ) называется величина, возможные значения которой непрерывно заполняют собой некоторый конечный или бесконечный интервал.

_{–функция распределения вероятностей случайной величины.}

Свойства F(x):

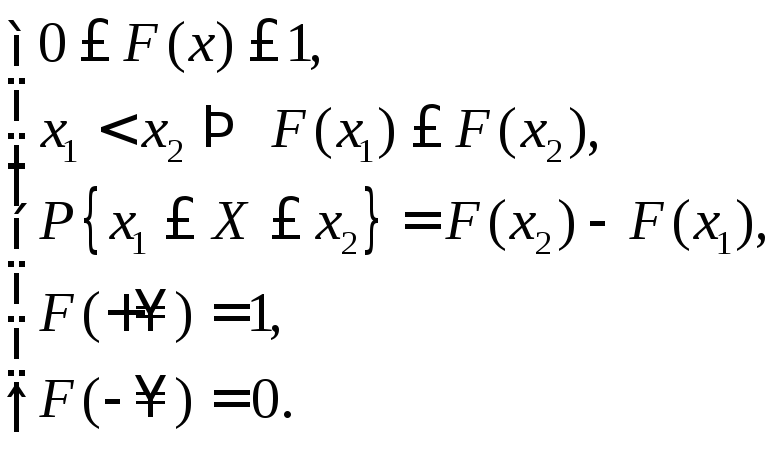
_{–плотность распределения вероятностей НСВ.}

Свойства f(x):

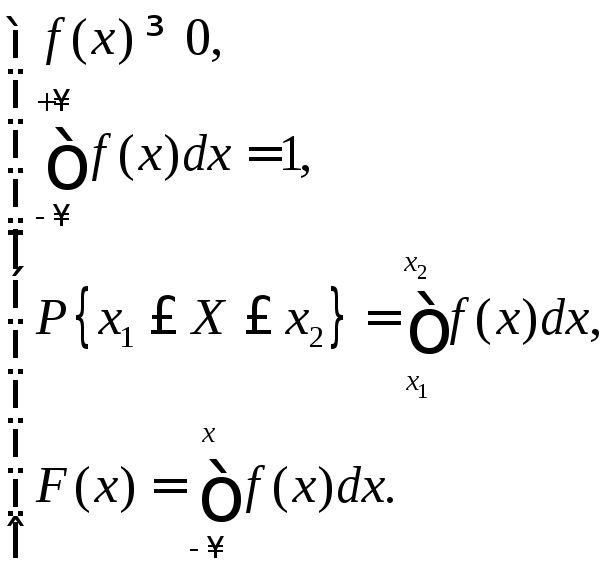
Числовые характеристики непрерывной случайной величины

1) Математическое ожидание:

2) Дисперсия:

3) Среднее квадратическое отклонение:

Виды распределения НСВ

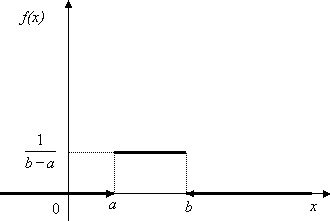
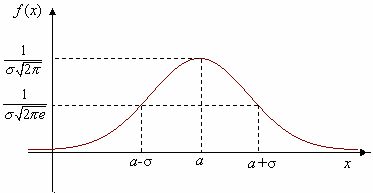
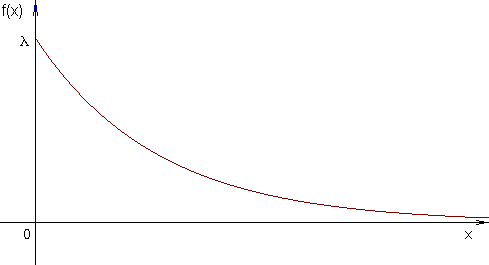
	Равномерное	Нормальное	Показательное
Плотность распределения
Функция распределения
Числовые характеристики
Вероятность попадания в интервал		Правило трёх сигм:

Закон больших чисел

Неравенство Чебышева:

Теорема Чебышева:,

где

Теорема Бернулли:

Элементы математической статистики

Выборочная средняя:

Дисперсия:

Среднее квадратическое отклонение:

Коэффициент вариации:

Мода:

–начало модального интервала (интервала с наибольшей частотой);

h – длина частичных интервалов;

–частота домодального интервала;

–частота модального интервала;

–частота замодального интервала.

Медиана:

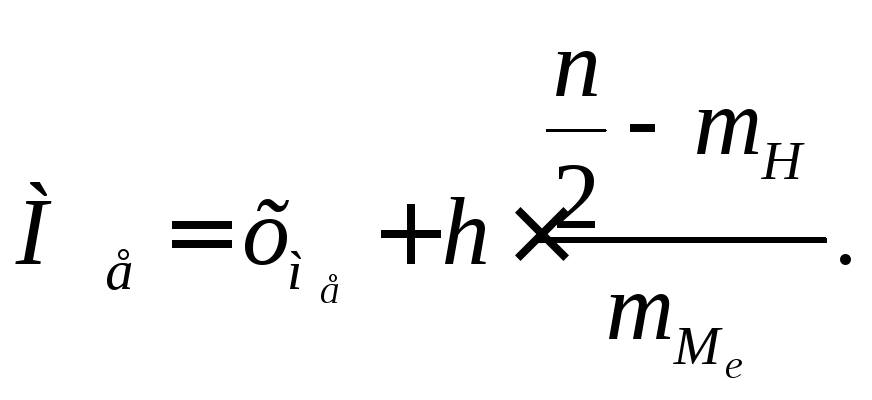
–начало медианного интервала;

h – длина частичных интервалов;

n – объём выборки;

–накопленная частота домедианного интервала;

–частота медианного интервала.

69