Справочные материалы аналитическая геометрия Прямая на плоскости

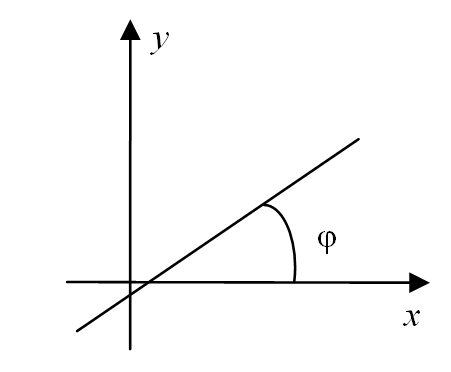φ – угол наклона прямой, φ∈ [0;π).

k=tg φ – угловой kоэффициент, k∈(-∞;+∞).

Стандартные уравнения прямой

1. Уравнение прямой с угловым коэффициентом:

k – угловой коэффициент прямой,

b – отрезок, отсекаемый прямой на оси Oy.

2. Уравнение прямой с известным угловым коэффициентом, проходящей через заданную точку:

k – угловой коэффициент прямой, – координаты заданной точки.

3. Уравнение прямой, проходящей через две заданные точки:

, – координаты заданных точек.

4. Общее уравнение прямой:

А, В, С – некоторые числа, причём А²+В²≠0.

Частные случаи уравнения:

y=b – уравнение прямой, параллельной оси Ox (y=0 – ось Ox).

x=a – уравнение прямой, параллельной оси Oy (x=0 – ось Oy).

y=kx – уравнение прямой, проходящей через начало координат.

Угол между прямыми

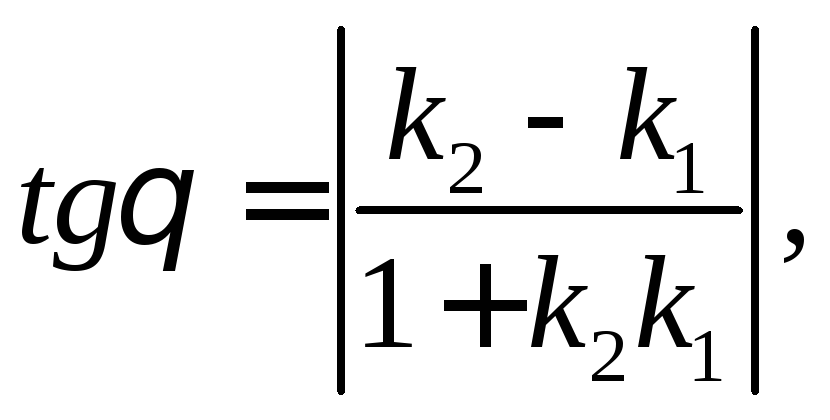где угловые коэффициенты прямых.

Условие параллельности прямых:

Условие перпендикулярности прямых:

Дифференциальное исчисление

Опр. Производной функции y=f(x) называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю:

Операция нахождения производной называется дифференцированием функции.

Геометрический смысл производной

Производная функции, вычисленная в точке х₀, равна угловому коэффициенту касательной, проведённой к графику функции в этой точке:

Биологический смысл производной

Пусть функция p=p(t) задаёт число особей в популяции в зависимости от времени t. Тогда производная этой функции, вычисленная в точке t₀, равна скорости размножения популяции (если она положительна, то это скорость размножения, если отрицательна – скорость вымирания) в момент времени t₀:

_{Правила дифференцирования}

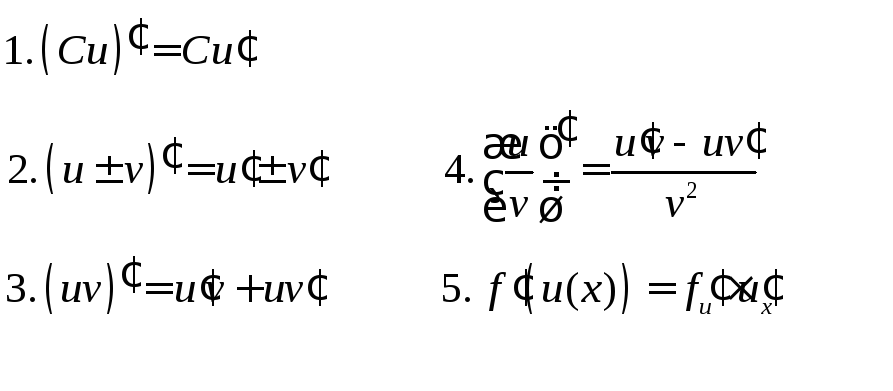
Таблица производных

Основные элементарные функции Сложные функции

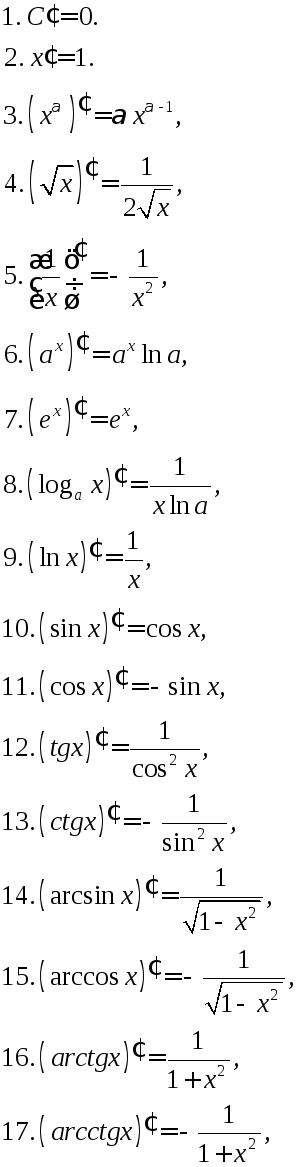
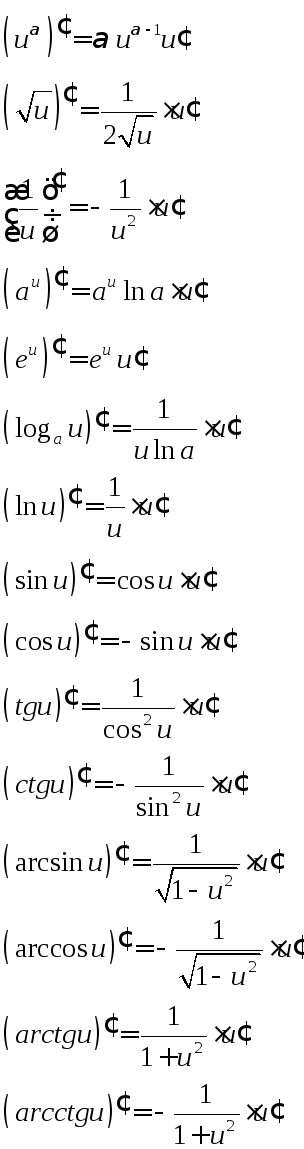
Интегральное исчисление

Опр. Функция F(x) называется первообразной для функции f(x), если выполнено равенство: .

Опр. Общее выражение множества всех первообразных для функции f(x) называется неопределённым интегралом от этой функции.

Опр. Операция нахождения первообразной называется интегрированием функции.

Свойства неопределённого интеграла

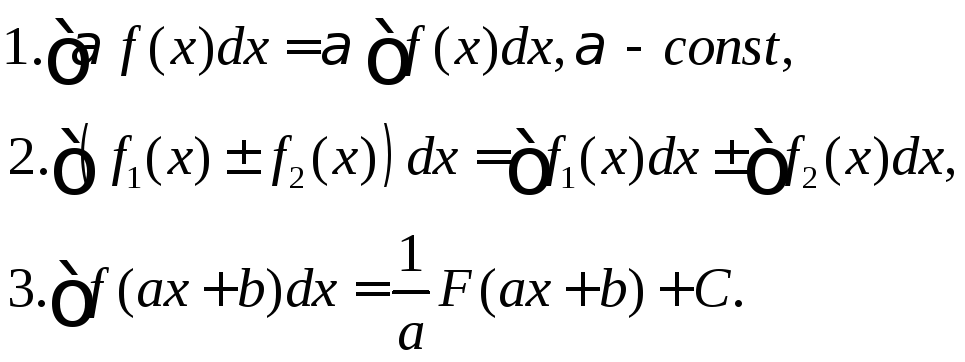
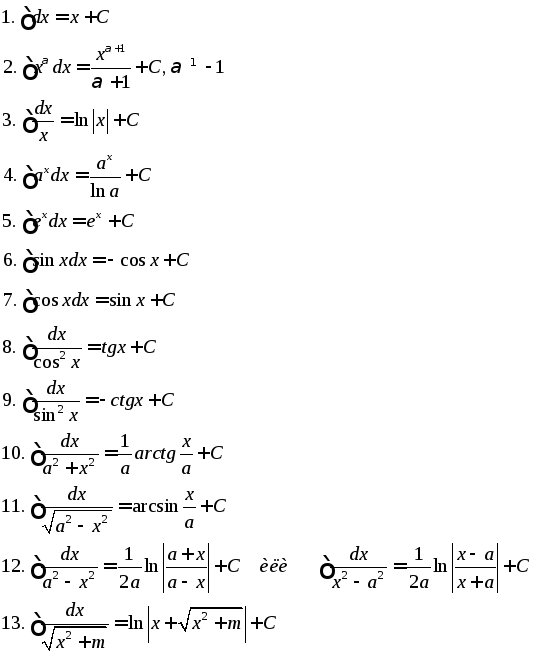
Таблица основных интегралов

Определённый интеграл

Опр. Пусть функция f(x) определена и непрерывна на отрезке [a;b]. Определённым интегралом от функции f(x) по отрезку [a;b] называется предел интегральной суммы приn→∞ и λ→0, не зависящий ни от способа разбиения отрезка, ни от выбора промежуточных точек х_i:

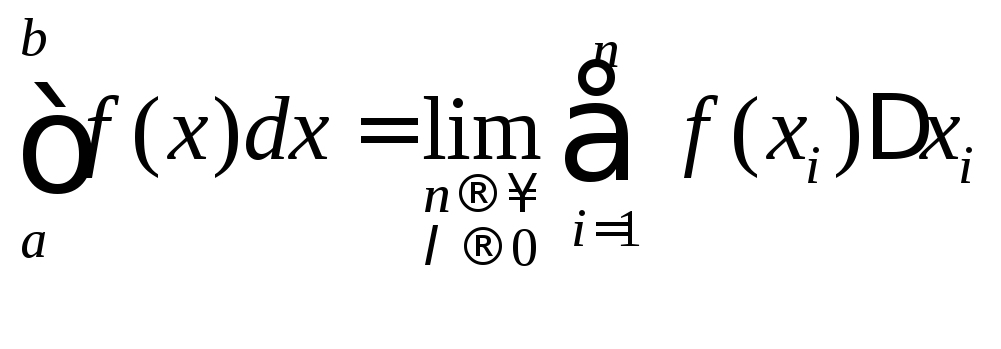
n – число отрезков, на которые разбит отрезок [a;b], λ – длина наибольшего отрезка, х_i – некоторая точка i-го отрезка.

Формула Ньютона-Лейбница:

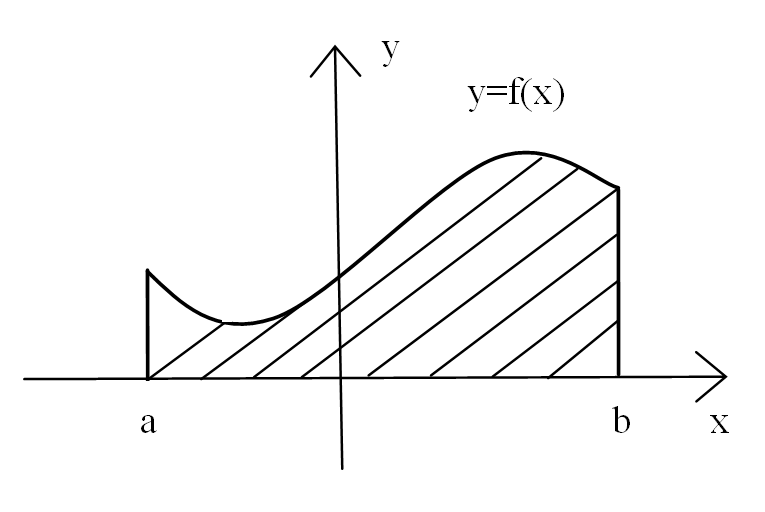
Геометрический смысл: Определённый интеграл равен площади криволинейной трапеции, ограниченной графиком непрерывной и неотрицательной на отрезке [a;b] функции y=f(x), прямыми x=a, x=b и осью Ox:

Свойства определённого интеграла

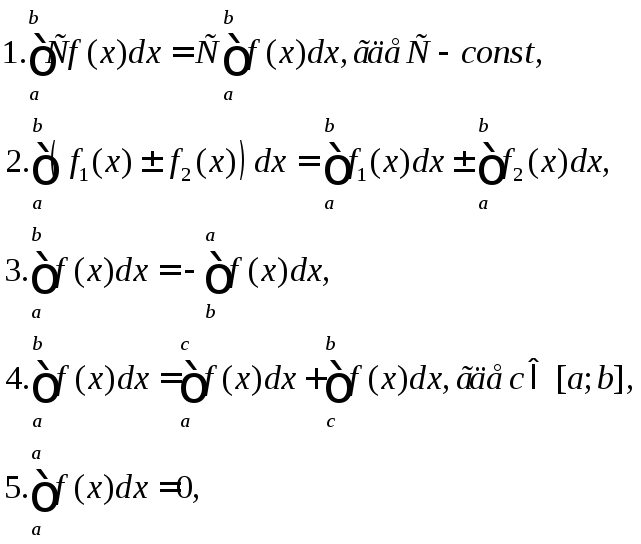
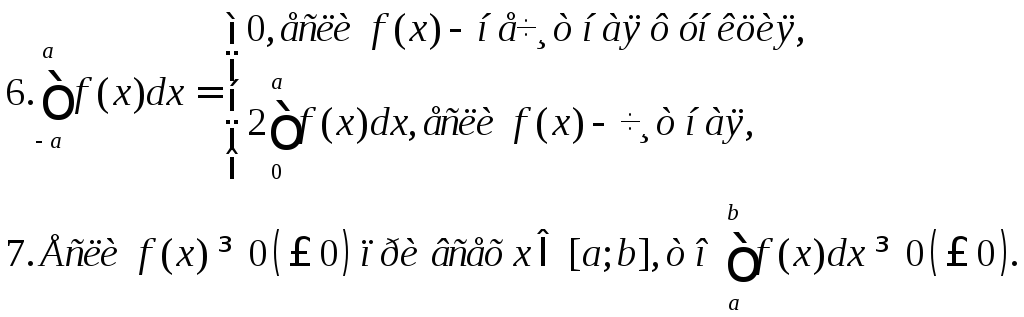
Геометрические приложения: площадь фигуры

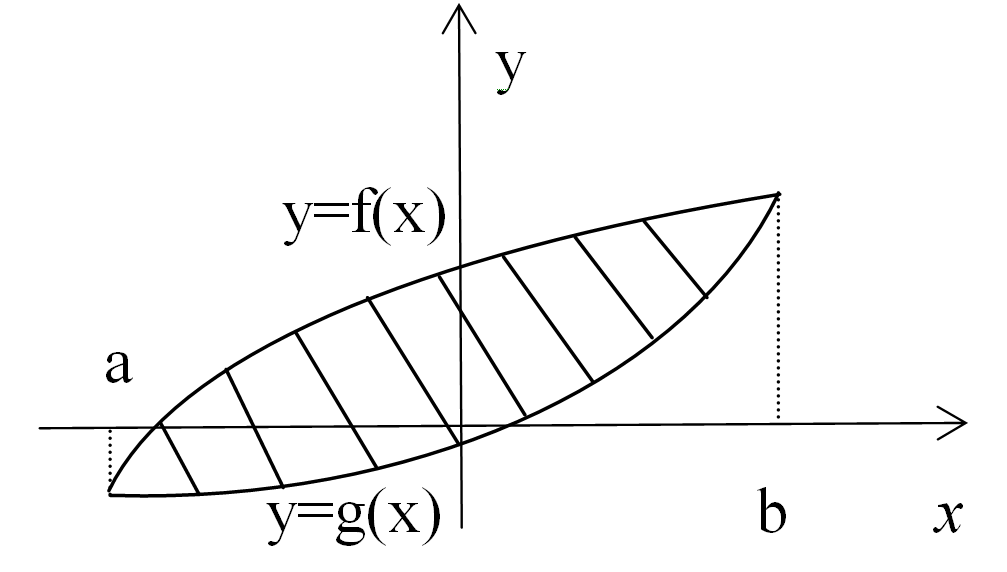
где a и b – абсциссы точек пересечения графиков, которые находят из уравнения f(x)=g(x).