Arkhiv_ZIP_-_WinRAR / Chast_5_DifUr

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Российский государственный профессионально-педагогический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

+4 = 0, y (1)= 0 .

Найти общее решение уравнения y′′= y′3 y .

Найти общее решение уравнения xy′2 + y′′= 0 .

Найти решение задачи Коши y′′+ y = tgx, y (0)= y′(0)=1.

.pdf

Скачиваний:

Добавлен:

29.05.2015

Размер:

1.09 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1211 12 > Следующая >>>

x (y′+1)=(x + y +2)2 , y (1)=1.

Найти общее решение уравнения y′

= tg

Найти решение задачи Коши для уравнения

y′+

+ x +1 = 0, y (1)= 0 .

′′

′

Найти общее решение уравнения y

= y y

Найти общее решение уравнения y′′+ xy′′′= 0 .

Найти решение задачи Коши y′′+ y =

y (0)= y′(0)=1.

cos x

8.Найти уравнение кривой, проходящей через точку (−1,1), если длина

отрезка полуоси абсцисс, отсекаемого её касательной, равна квадрату абсциссы точки касания.

9.Решить систему при заданных начальных условиях

	x′	(	t	)	= y +t
	x′		t		= y +t	,	x (0)= 0, y (0)=1.
y′(t )= 2x + y						,	x (0)= 0, y (0)=1.

Вариант 16

1. Решить дифференциальное уравнение sin xdy −cos ydx = 0 .

2.Найти решение задачи Коши для уравнения

x(2 y′+1)=(x +2 y )2 , y (1)=1.

3.Найти общее решение уравнения y′ = xy + xy .

4.Найти решение задачи Коши для уравнения

8.Количество света, поглощаемого тонким слоем воды на определённой глубине, пропорционально количеству света на этой глубине. Известно, что слой воды в 1 м поглощает 40% падающего света. Какую часть света поглотит слой толщиной 3 м?

9.Решить систему при заданных начальных условиях

	x′	(	t	)	= −y +1
	x′		t		= −y +1	,	x (0)= 0, y (0)=1.
y′(t )= −2x + y +t						,	x (0)= 0, y (0)=1.

101

Вариант 17

1.Решить дифференциальное уравнение sin xdy −tgydx = 0 .

2.Найти решение задачи Коши для уравнения

y (0)=1.

y′=

−2 ,

arcsin (2x + y)

Найти общее решение уравнения yy′ =

x 2

Найти решение задачи Коши для уравнения y′+2xy + x3 = 0, y (0)=1.

′′ ′

= e

Найти общее решение уравнения 2 y y

Найти общее решение уравнения

y′2 +2 yy′′= 0 .

Найти решение задачи Коши y

′′

+ y

′

y (0)

′

(0)=1.

1+ex

= y

8.Найти уравнение кривой, проходящей через точку (−1,1), если длина

отрезка полуоси абсцисс, отсекаемого её нормалью, на 2 больше абсциссы точки касания.

9.Решить систему при заданных начальных условиях

	x′	(	t	)	= y + x
	x′		t		= y + x	,	x(0)= 0, y (0)=1.
y′(t )= x + y +t						,	x(0)= 0, y (0)=1.

Вариант 18

1.Решить дифференциальное уравнение sin xdy −(y2 +1)dx = 0 .

2.Найти решение задачи Коши для уравнения

y (0)=1.

y′=

−2 ,

arctg (2x + y)

Найти общее решение уравнения y′ =

−

Найти решение задачи Коши для уравнения

y′−2xy + xex2 = 0, y (0)=1.

′′

′

+ x .

Найти общее решение уравнения y y

Найти общее решение уравнения

y′′

= y′

y′

Найти решение задачи Коши y′′− y′=

y (0)= y′(0)=1.

+e−x

8.Скорость остывания тела пропорциональна разности температур тела и окружающей среды. За 40 мин тело охладилось от начальной темпера-

102

ex+y

туры в 300° до 150°. Температура окружающей среды равна 50°. Сколько времени тело остывает от начальной температуры до 100°?

9. Решить систему при заданных начальных условиях

		(	t	)	= −y +2x −1
x′			t		= −y +2x −1	,	x(0)= 0, y (0)=1.
	y′		(t )= 2x − y +t			,	x(0)= 0, y (0)=1.

Вариант 19

1.Решить дифференциальное уравнение (x3 +1)dy −(y +1)dx = 0 .

2.Найти решение задачи Коши для уравнения

	y′=	1	+2x + y ,		y (0)=1.
		2x + y
3.	Найти общее решение уравнения			y′ = 2		y	+	y	.

								x
						x

4.	Найти решение задачи Коши для уравнения
	y′+ x y + x = 0, y (0)=1.
5.	′′	′3	.
	Найти общее решение уравнения y y = y
6.	Найти общее решение уравнения xy′′+ y′= y′2 .
7.	Найти решение задачи Коши y′′− y′= 2x , y (0)= y′(0)=1.

8.Найти уравнение кривой, проходящей через точку (1,3), если длина

отрезка полуоси абсцисс, отсекаемого любой её касательной, равна длине этой касательной.

9.Решить систему при заданных начальных условиях

	(	t	)	= y + x −1
x′		t		= y + x −1	,	x(0)= 0, y (0)=1.
y′(t )= 2x − y +t					,	x(0)= 0, y (0)=1.

Вариант 20

1.Решить дифференциальное уравнение (x3 +1)dy − 3 y +1dx = 0 .

2.Найти решение задачи Коши для уравнения

y′= x + y −1, y (0)=1.

3.	Найти общее решение уравнения		y		y	.
		y′ =		+ 2
					x
			x

4.	Найти решение задачи Коши для уравнения y′−tgxy + x = 0, y (0)=1.
5.	Найти общее решение уравнения xy′′2 = y′.
6.	Найти общее решение уравнения y′+ y y′′ = 0 .

103

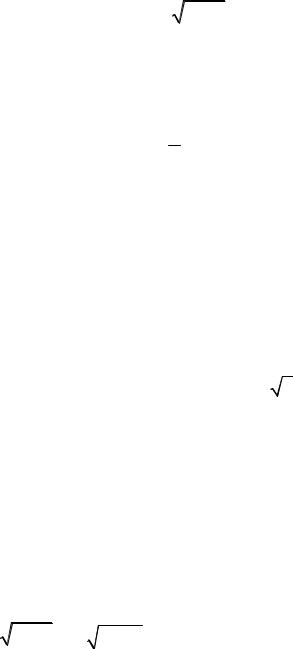
7. Найти решение задачи Коши y′′− y =5x , y (0)= y′(0)=1.

8.Известно, что предельная скорость падения парашютиста в воздухе без раскрытия парашюта равна 50 м/с. За какое время он достигает этой

скорости, покинув самолёт, если известно, что сила сопротивления воздуха пропорциональна квадрату его скорости падения ( k = 0.07 кг/м)? Принять g =10 м/с2, а вес парашютиста равным 70 кг.

9.Решить систему при заданных начальных условиях

x′

(

)

= y − x −2

x(0)= 0, y (0)=1.

y′(t )=3x + y +2t ,

Вариант 21

Решить дифференциальное уравнение (

1− x2 )dy −

dx = 0 .

ln y

Найти решение задачи Коши для уравнения

y′

x + y −1

−1,

y (0)= 2 .

ln (x + y −1)

3.Найти общее решение уравнения y′ = y 2 + 2 .

4.Найти решение задачи Коши для уравнения

	y′+ сtgxy + x = 0,	π
		y =1 .
		2	y′′				y′
5.	Найти общее решение уравнения				+				= 0 .
							y +	1
			y′
6.	Найти общее решение уравнения			x		+ y′′= 0 .
				y′
7.	Найти решение задачи Коши y′′−2 y′+2 = ex , y (0)= y′(0)=1.

8.Найти уравнение кривой, проходящей через точку ( 2,1), если

произведение абсциссы отрезка, отсекаемого её касательной, и абсциссы точки касания есть величина постоянная, равная 1.

9.Решить систему при заданных начальных условиях

	x′	(	t	)	= −y −2
	x′		t		= −y −2	,	x(0)= 0, y (0)=1.
y′(t )= x +2 y +t						,	x(0)= 0, y (0)=1.

Вариант 22

1.Решить дифференциальное уравнение

1− x2 dy − 4 y +2 arccos xdx = 0 .

2.Найти решение задачи Коши для уравнения

104

y′=32 x+y −2 , y (0)=1.

Найти общее решение уравнения y′ =

2 +

Найти решение задачи Коши для уравнения y′

+ x = 0,

y (0)=1.

x +1

Найти общее решение уравнения

y′′

= 0 .

x2 +1

y′

′

′′ 2

Найти общее решение уравнения

−

= 0 .

y +1

y′

Найти решение задачи Коши y′′+ y = ln (sin x),

= y′

=1.

8.Тело с начальной скоростью 2 м/с движется в среде, в которой сила сопротивления пропорциональна скорости тела. Через 5 с её скорость оказалась равна 1 м/с. Когда скорость тела уменьшится до 0.1 м/с?

9.Решить систему при заданных начальных условиях

′

(

)

= 2 y −2t

x t

x(0)= 0, y (0)=1.

y′(t )= x

+ y +t ,

Вариант 23

Решить дифференциальное уравнение

(1+ x2 )dy −ey arctgxdx = 0 .

Найти решение задачи Коши для уравнения

y′=(x −2 y)

, y (0)=

ctg

x −2 y

2π

Найти общее решение уравнения y′ = 2

Найти решение задачи Коши для уравнения

y′+

+ x

= 0,

y (0)=1.

x +2

y′′

Найти общее решение уравнения

−

y = 0 .

y′

Найти общее решение уравнения

y′′

−

= 0 .

y′+1

Найти решение задачи Коши

y′′+ y′= ex ln (ex +1),

y (0)= y′(0)=1.

8.Найти уравнение кривой, проходящей через точку ( 5,1), если

произведение абсциссы отрезка, отсекаемого её касательной, и абсциссы точки касания есть величина постоянная, равная 4.

105

9. Решить систему при заданных начальных условиях
x′		(	t	)	= −y −cost
		(		)		,	x(0)= 0, y (0)=1.
	y′(t )= −2x + y					,	x(0)= 0, y (0)=1.

		Вариант 24
1.	Решить дифференциальное уравнение			ln (1+ y)dy −	1+ y dx = 0 .
2.	Найти решение задачи Коши для уравнения				2 − x

	y′=	x −2 y −1	1	, y (0)=1.
			+ 2
		(x −2 y)2

3.Найти общее решение уравнения y′ = yy +− xx + xy .

4.Найти решение задачи Коши для уравнения

′

+ x +1 + x +1 = 0, y (0)=1.

y′′

′2

Найти общее решение уравнения

− y

= 0 .

Найти общее решение уравнения

y′′

y′

−

= 0 .

y′

y +1

Найти решение задачи Коши y′′+2 y′=

y (0)= y′(0)=1.

ex +1

8.Футбольный мяч весом 0.4 кг падает с высоты 45 м без начальной скорости. Считая, что сопротивление воздуха пропорционально

квадрату скорости ( k = 0.01кг/м), найти время падения мяча. Принять g =10 м/с2.

9.Решить систему при заданных начальных условиях

′

(

)

= −y −3t

x t

x(0)= 0, y (0)=1.

y′(t )= −2x + y +1,

Вариант 25

Решить дифференциальное уравнение xdy −

1+ y

dx = 0 .

Найти решение задачи Коши для уравнения

2 − x

y′= 2x + y , y (0)=1.

Найти общее решение уравнения y′ =

y 2 + x2

y 2 − x2

106

4. Найти решение задачи Коши для уравнения
y′+	y		x		π
		+ x cos		= 0,	y	=1.
	sin x		2
					2

5.	Найти общее решение уравнения	y3 y′′ − yy′= 0 .
6.	Найти общее решение уравнения	y′′	−	y′		=	1	.
				y +	1		x +1
		y′
7.	Найти решение задачи Коши y′′+4 y′+4 y = x +sin x, y (0)= y′(0)=1.

8.Найти уравнение кривой, проходящей через точку ( 10,1), если

произведение абсциссы отрезка, отсекаемого её касательной, и абсциссы точки касания есть величина постоянная, равная 9.

9.Решить систему при заданных начальных условиях

	(	t	)	= −x − y −3t
x′					,	x	(	0	)	= 0, y	(	0	)	=1.
		y′(t )= x + y

107

V.ОБРАЗЕЦ КОНТРОЛЬНОЙ РАБОТЫ

1.Найти общий интеграл уравнения xyy′=1−x2 . Ответ: x2 + y2 = 2ln x +С.

2. Найти решение задачи Коши: xy′+ y −ex = 0, y(a)= b .

Ответ: y = ex −ea + ab . x

3.Найти общее решение уравнения y′+ y cos x = sin xcos x .

Ответ: y = e−sin x esin x (−1+sin x)+ C =−1+sin x +Ce−sin x .

4.Найти общее решение уравнения 2xy′y′′=(y′)2 +1.

Ответ: y = ± 2 (xC1 −1)2 +C2 .

C1 3

3		′′			( )		′	( )
	y		+9	= 0,	y 1 =1,	y		1	= 3 .
5. Найти решение задачи Коши: y

Ответ: y = 6x −5 .

6.Найти общее решение уравнения y′′+3y′+ 2 y = 2ex cos 2x .

Ответ: y = C1e−x +C2e−2 x + 6298 ex 23cos 2x +10sin 2x .

108

VI. ФОРМУЛЫ

Решение ДУ первого порядка

Вид уравнения

Тип уравнения

Метод решения

P( x )dx +Q( y )dy = 0

с разделяющимися

непосредственное

переменными

интегрирование

y′=

однородное

u =

y = u x ,

y′ = u′ x +u

y′=

a1x + b1 y + c1

обобщенное

x = X +α,

однородное

x + b

y + c

y =Y + β;

a α +b β + c = 0,

a2α +b2β + c2 = 0;

y′

=Y ′

y′= P( x )y +Q( x )

линейное по y( x )

y = u υ

′

= uυ

′

+u υ

x′= P( y )x +Q( y )

линейное по x( y )

x = u υ

′

= u υ +uυ

y′+ P( x )y =Q( x ) yn

Бернулли

y = u

P( x,y )dx +Q( x,y )dy = 0

уравнение в полных

интегрирование

∂P

= ∂Q , du( x, y ) = 0

дифференциалах

∂u

= P( x, y ),

∂x

∂y

∂x

системы

∂u

=Q( x, y )

∂y

Решение ДУ второго порядка, допускающих понижение порядка

			Вид ДУ			Метод решения
1.	y′′=			f (x)		Последовательное интегрирование
2.	y′′ = f (x, y′)					p( x ) = y′, p′ = y′′
		′′	=	′			dp
3.	y			f (y, y	)	p( y ) = y′, y′′ =		p
							dy

109


4.	y′′ =	y − xy′	p =	y	,	p′ = −	y − xy′
		x2		x			x2
5.	yy′′+ y′2 = x		p = yy′, p′ = y′2 + yy′′

Решение ОЛДУ второго порядка с постоянными коэффициентами

y′′+ py′+ qy = 0, k2 + pk + q = 0.

Корни характеристического уравнения

Вид общего решения

y = c1ek1x +c2ek2 x

1. D > 0,k

= −

−q ,

1,2

действительные, разные

2. k1

= k2 = k = −

y = (c1 + c2 x)ekx

действительные, равные, кратность 2

3. k

=α ±i

β,α = −

β = q −

y = eαx (c1cosβ x +c2sinβ x)

1,2

комплексные

4. k1,2 = ±iβ,α = 0

y = c1cosβ x +c2sinβ x

ОЛДУ n-го порядка с постоянными коэффициентами

y( n ) + a y( n−1 ) + a

y( n−2 )

+ ...+ a

= 0, a

= const,

kn + a kn−1 + a

kn−2

+ ...+ a

= 0 .

Корни характеристического урав-

Вид общего решения

нения

1. Действительные, различные

Общее решение

k1 ≠ k2 ≠ k3 ≠ ... ≠ kn

y = c ek1x +c ek2 x +...+c ekn x

2. Действительные, кратности

Вклад в общее решение от веществен-

r ≤ n k1 = k2 = k3 = ... = kr = k

ного корня кратности r

y =(c1 +c2 x +c3 x2 +...+cr xr−1 )ekx

3. Комплексные, различные,

Вклад в общее решение от различных-

k1 =α1 +i β1 ,k2 =α2 +i β2 ,...,

комплексных корней

km =αm +i βm , α1 ≠α2 ≠ ... ≠αm ,

β1 ≠ β2 ≠ ... ≠ βm .

110

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1211 12 > Следующая >>>

Соседние файлы в папке Arkhiv_ZIP_-_WinRAR

#
29.05.20151.95 Mб20Chast_1_Opredeliteli_Matritsy_Sistemy.pdf
#
29.05.20154.52 Mб28Chast_2_Vekt_i_anal_2010_07_29.pdf
#
29.05.20154.89 Mб21Chast_3__Mat_an_2010_23_09.pdf
#
29.05.20151.09 Mб39Chast_5_DifUr.pdf
#
29.05.2015934.06 Кб28Chast_6_FNP.pdf
#
29.05.2015608.76 Кб18Модуль 2_4 Формулы пр.pdf