Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Российский государственный профессионально-педагогический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Arkhiv_ZIP_-_WinRAR / Chast_1_Opredeliteli_Matritsy_Sistemy

.pdf

Скачиваний:

Добавлен:

29.05.2015

Размер:

1.95 Mб

Скачать

☆

1 / 111 2 3 4 5 6 7 8 9 10 11 > Следующая >>>

Министерство образования и науки Российской Федерации Уральский федеральный университет

имени первого Президента России Б.Н. Ельцина

Кафедра высшей математики

МАТЕМАТИКА

Часть 1. АЛГЕБРА

Научный редактор – доц., канд. физ.-мат. наук Л.П. Мохрачева

Рекомендовано Уральским отделением Учебно-методического объединения вузов РФ в области строительного образования в качестве учебного пособия для студентов специальностей направления 6533500

«Строительство» всех форм обучения

Екатеринбург

УрФУ

2010

УДК 512.643(075.8) ББК 22.143я 73 М 33

Рецензенты:

кафедра физики Уральского государственного лесотехнического университета; доктор физ.-мат. наук, проф. А.П. Танкеев, зав. лабораторией ИФМ УрО РАН.

Авторы: Соболев А.Б., Вигура М.А., Рыбалко А.Ф., Рыбалко Н.М., Батекина И.А., Мохрачева Л.П.

М 33 МАТЕМАТИКА. Ч.1. Алгебра: учебное пособие / Соболев А.Б., Вигура М.А., Рыбалко А.Ф., Рыбалко Н.М., Батекина И.А., Мохрачева Л.П. Екатерин-

бург: УрФУ, 2010. 108с.

ISBN 978-5-321-01783-8

Данное пособие представляет собой первую часть базового курса высшей математики и предназначено для бакалавров, программа обучения которых предусматривает равные количества аудиторных часов и часов для самостоятельной работы студентов.

Содержание пособия охватывает следующие разделы программы: основы теории матриц и определителей, решения систем линейных уравнений.

Пособие включает теоретические сведения, примеры решения задач, тексты домашних заданий, титул и текст индивидуальной расчетной работы, образец контрольной работы и справочный материал по теме.

Подготовлено кафедрой высшей математики

УДК 512.643(075.8) ББК 22.143я 73

ISBN 978-5-321-01783-8

	ОГЛАВЛЕНИЕ
1.	МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ..........................................................................	4
	1.1. Матрицы......................................................................................................	4
	1.1.1. Определение матрицы. Виды матриц...................................................	4
	1.1.2. Операции над матрицами и их свойства ..............................................	5
	1.2. Определители второго, третьего и n-го порядков..................................	7
	1.2.1. Определения определителей 2-го, 3-го и n - ого порядков ................	7
	1.2.2. Свойства определителей........................................................................	9
	1.2.3. Методы вычисления определителей произвольного порядка..........	11
	1.3. Обратная матрица....................................................................................	14
	1.4. Матричные уравнения.............................................................................	16
	1.5. Ранг матрицы............................................................................................	17
2.	СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ...........................................................	19
	2.1. Системы m линейных уравнений с n неизвестными............................	19
	2.2. Решение систем n линейных уравнений с n неизвестными методом
	Крамера ....................................................................................................	20
	2.3. Схема отыскания решения системы m линейных уравнений с n
	неизвестными...........................................................................................	21
	2.4. Решение систем линейных уравнений методом Гаусса.......................	23
	2.5. Однородные системы ..............................................................................	24
3.	ПРАКТИЧЕСКИЕ ЗАНЯТИЯ..............................................................................	28
	3.1. Определители второго и третьего порядка и их свойства...................	28
	3.2. Определители n–го порядка....................................................................	32
	3.3. Матрицы и действия с ними...................................................................	36
	4.4. Системы линейных уравнений...............................................................	44
4.	ДОМАШНИЕ ЗАДАНИЯ.....................................................................................	58
	ДЗ № 1. Матрицы и определители................................................................	58
	ДЗ № 2. Системы линейных уравнений........................................................	61
5.	РАСЧЕТНАЯ РАБОТА.........................................................................................	63
6.	ПРИМЕР ВАРИАНТА КОНТРОЛЬНОЙ РАБОТЫ..........................................	94
7.	ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ФОРМУЛЫ..................................................	95
8.	БИБЛИОГРАФИЧЕСКИЙ СПИСОК................................................................	107

1. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ

1.1.Матрицы

1.1.1.Определение матрицы. Виды матриц

ОПРЕДЕЛЕНИЕ. Матрицей размера m ×n называется прямоугольная таблица

чисел aij , i =1, 2,..., m ;		j =1,2,..., n , расположенных в m строках и n столбцах:
		a11	a12		… a1n
			a22		…
		a21	a22		…	a2n
		A =				.
			am2		…
		am1	am2		…	amn
Числа aij	называются элементами матрицы.
Матрица	размера	1×n называется			матрицей-строкой и		имеет вид:
А= (a1 a2	a3 ...an )1,n . Матрица		размера			m ×1 называется	матрицей-
столбцом и имеет вид:				a1
				a1
				a
				2
		В = ...			.

				am

ОПРЕДЕЛЕНИЕ. Матрица называется квадратной, если число строк равно числу столбцов ( m = n ), при этом число n называется порядком матрицы. Пример квадратной матрицы 3-го порядка:

	a 1 1	a 1 2	a 1 3
A =	a 2 1	a 2 2	a 2 3

	a 3 1	a 3 2	a 3 3	.

ОПРЕДЕЛЕНИЕ. Ряд элементов квадратной матрицы, лежащих на отрезке, соединяющем левый верхний угол с правым нижним, называется главной диагональю, а на отрезке, соединяющем правый верхний угол с левым нижним, –

побочной диагональю матрицы.

ОПРЕДЕЛЕНИЕ. Квадратная матрица, у которой все элементы, стоящие ниже (или выше) главной диагонали, равны нулю, называется верхней (нижней) треугольной; пример верхней треугольной матрицы третьего порядка:

a		a
	11	12
	0	a22
	0	0
	0	0

a13

a23 . a33

ОПРЕДЕЛЕНИЕ. Квадратная матрица, у которой все элементы, стоящие выше и ниже главной диагонали, равны нулю ( aij = 0 при i ≠ j ), называется

диагональной:

a		0	...	0
	11	a22	...	0
	0
...		...	...	...	.
	0	0	...
				ann

Очевидно, что диагональная матрица является одновременно и верхней треугольной, и нижней треугольной.

ОПРЕДЕЛЕНИЕ. Квадратная диагональная матрица с единичными элементами на диагонали называется единичной и обозначается буквой Е. Например, единичная матрица 3-го порядка имеет вид:

	1	0	0
E =	0	1	0
				.
	0	0	1

ОПРЕДЕЛЕНИЕ. Если все элементы матрицы равны нулю, то матрица называется нулевой и обозначается O .

ОПРЕДЕЛЕНИЕ. Матрицы A и B называются равными, если они имеют одинаковые размеры и все их соответствующие элементы совпадают.

1.1.2.Операции над матрицами и их свойства

1.Сложение матриц

ОПРЕДЕЛЕНИЕ. Суммой матриц		A = (aij ) и	B = (bij ) одинаковой размер-
ности m ×n называется матрица		C = A + B ,	элементы которой равны
cij = aij +bij , где i =1, 2,..., m ; j =1,2,..., n .
Свойство 1 .	A + B = B + A.
Свойство 2 .	(A + B)+C = A +(B +C ).
Свойство 3 .	A +O = A .
2. Умножение матрицы на число
ОПРЕДЕЛЕНИЕ. Произведением матрицы A на число α называется мат-

рица C =αA ,	элементы которой удовлетворяют условию: cij =αaij , где
i =1, 2,..., m ; j =1,2,..., n .
Свойство 4.	A +(−A)=O .
Свойство 5.	(αβ)A =α (β A).
Свойство 6. α (A + B)=αA +αB .
Свойство 7.	(α + β)A =αA + β A .
Свойство 8.	0 A =O ; 1 A = A .

2		1	−1	,	−2		1	0
ПРИМЕР: Найдите 3A + 2B , если A =	0	1	−4		B =	−3	2	2	.

6		3	−3 −4			2	0	2 5		−3
Решение: 3A + 2B =	0	3	−12	+	−6	4	4	=	−6 7	−8	.

3. Умножение матриц

ОПРЕДЕЛЕНИЕ. Произведением матрицы A размерности (m×n) на мат-

рицу B размерности (n×k) называется матрица C=AB размерности (m×k), элементы которой находятся по формуле:

cij = ∑aiqbqj = ai1b1 j +ai2b2 j +…+ainbnj , где i =1, 2,..., m ; j =1, 2,..., k , q=1

т.е. элемент cij равен сумме произведений элементов i–й строки матрицы A на

элементы j–го столбца матрицы B. Число столбцов первой матрицы должно равняться числу строк второй матрицы.

												4	1
ПРИМЕР: Найдите АВ, если A = (1												5	2
ПРИМЕР: Найдите АВ, если A = (1							2 3) , B =					5	2	.
												6	3
												6	3
Решение: C = AB = (1 4 + 2 5 +3 6							1 1 + 2 2 +3 3)= (32 14),
размерность матрицы C (1×2).
Свойство 9.	(AB)C = A(BC ).
Свойство 10.	(A + B)C = AC + BC .
Свойство 11.		A(B +C )= AB + AC .
ОПРЕДЕЛЕНИЕ. Матрицы A и B называются перестановочными (ком-
мутирующими), если AB = BA .
В общем случае произведение матриц не коммутативно: AB ≠ BA.
									1	2			1	2
ПРИМЕР: Найдите AB и BA, если A =									3	4	, B =			2	.
									3	4			1	2
		1 2 1 2				3 6					1 2				1 2 7 10
Решение: A B =				=				, B A			=				=	7 10	.
		3 4 1 2				7 14					1 2				3 4	7 10
Свойство 12.		AE = EA = A.
Свойство 13.		AO =OA =O .
4. Транспонирование матрицы
ОПРЕДЕЛЕНИЕ. Если A =			(aij )			, то транспонированная матрица AT											оп-
					m,n
ределяется равенством:			= (a′ )					, где aij′			= a ji .
		AT	= (a′ )					, где aij′			= a ji .
					ij	n,m

Иными словами, строки матрицы становятся столбцами с теми же номерами, а столбцы – строками:

Свойство 14.

	a	a	…	a			a11	a21 … am1
	11	12		1n
	a21	a22	… a2n		T		a12	a22 … am2
A =					A	=									,
		am2						a2n		… amn
	am1	am2	…	amn m,n			a1n	a2n		… amn				n,m
Например, для												1		4
						1	2	3				1		4
						1	2	3		T	=		2	5	.
					A =			6	,	A	=		2	5	.
						4 5		6
												3		6

ОПРЕДЕЛЕНИЕ. Если квадратная матрица A совпадает со своей транспо-

нированной, т.е. AT = A , то такая матрица называется симметрической. ОПРЕДЕЛЕНИЕ. Если квадратная матрица A отличается множителем −1 от

своей транспонированной, т.е. AT = −A , то такая матрица называется кососим-

метрической.

Операция транспонирования имеет следующие свойства:

(AT )T = A

Свойство 15. (A + B)T = AT + BT

Свойство 16. (AB)T = BT AT .

1.2. Определители второго, третьего и n-го порядков

1.2.1. Определения определителя 2-го, 3-го и n-го порядков

ОПРЕДЕЛЕНИЕ. Определителем второго порядка квадратной матрицы

Α= 11

называется число, равное a11a22 −a12a21 и обозначаемое

a21

a22

∆ =

= d e t Α =

a1 1

a1 2

= a1 1 a 2 2

− a1 2 a 2 1 .

a 2 1

a 2 2

ПРИМЕР:

=1 4 −3 2 = −2 .

ОПРЕДЕЛЕНИЕ. Определителем третьего порядка квадратной матрицы

a	a	a
11	12	13
A = a21	a22	a23
	a32
a31	a32	a33

называется число, равное

a11 a12 a13

∆ = Α = det Α = a21 a22 a23 =

a31 a32 a33

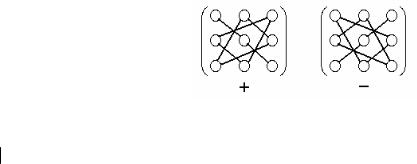
= a11a22 a33 + a12 a23 a31 +a13 a21a32 −a13 a22 a31 −a12 a21a33 −a11a23 a32 .

Это выражение получается по правилу треугольников (правилу Саррюса), его можно пояснить следующими схемами, на которых элементы, входящие в одно произведение с указанным знаком, соединены отрезками.

ПРИМЕР:

		1	−4	2			(		)	(	)	(		)		(		)		(	)		(		)		.
		1	−4	2
		0	3		1
Α	=	−2		−		=1 3 5 +		−4			−1		−2		+ 2 0 1 − 2 3		−2		−1		−1	1 −		−4		0 5 = 20
		−2	1	5

Чтобы дать определение определителя n-го порядка, нужно ввести некоторые новые понятия.

ОПРЕДЕЛЕНИЕ. Перестановкой из n чисел 1,2,…, n называется всякое расположение этих чисел в определённом порядке. Число перестановок из n чисел равно n!.

ОПРЕДЕЛЕНИЕ. Числа i, j составляют инверсионную пару в перестановке, если i>j, но i встречается в перестановке раньше, чем j.

ОПРЕДЕЛЕНИЕ. Перестановка называется чётной, если число инверсионных пар чётно, и нечётной, если - нечётно.

ОПРЕДЕЛЕНИЕ. Преобразование перестановки, при котором меняются местами два символа, называется транспозицией.

Теорема. Всякая транспозиция меняет чётность перестановки.

Две перестановки, записанные другом под другом, образуют подстановку. Канонической подстановкой называется подстановка вида

1	2	3	...	n
α1	α2	α3	...	.
α1	α2	α3	...	αn

Число инверсионных пар в обеих перестановках, образующих подстановку, определяет чётность подстановки. Справедливо утверждение: транспозиция не

изменяет четности подстановки.

Введённые выше понятия позволяют дать определение определителя любого порядка в общем виде:

ОПРЕДЕЛЕНИЕ. Определителем n-го порядка называется алгебраическая сумма n! слагаемых, каждое из которых есть произведение элементов матрицы, взятых по одному из каждой строки и каждого столбца, причём слагаемое входит со знаком плюс, если подстановка, образованная индексами элементов матрицы чётная, и со знаком минус – если нечётная.

Согласно этому определению определитель n-го порядка записывается в виде

	a11	a12	… a1n
	a11	a12	… a1n
	a21	a22	… a21		= ∑(−1)s(π )a1α1 a2α2 …anαn ,
	…	… … …				π
	an1	an2	… an3
				1		2	3	...	n
где s(π)- чётность подстановки				α1		α2	α3	...	.
				α1		α2	α3	...	αn

1.2.2. Свойства определителей

Перечислим свойства определителей, которые справедливы для определителей любого порядка. Для наглядности эти свойства проиллюстрированы на примерах определителей третьего порядка.

Свойство 1 . Определитель матрицы А не меняется при ее транспонировании: AT = A .

Свойство 2 . При перестановке местами двух строк (столбцов) определитель меняет знак:

a11	a12	a13	(α1 )	a21	a22	a23	(α2 )

a21	a22	a23	(α2 )= −	a11	a12	a13	(α1 )
a31	a32	a33	(α3 )	a31	a32	a33	(α3 ) .

Свойство 3 . Определитель, содержащий две одинаковые строки (два одинаковых столбца), равен нулю.

Свойство 4. Общий множитель для элементов некоторой строки (столбца) определителя можно вынести за знак определителя:

k a1 1	a1 2	a1 3		a1 1	a1 2	a1 3
k a1 1	a1 2	a1 3		a1 1	a1 2	a1 3
k a 2 1	a 2 2	a 2 3	= k	a 2 1	a 2 2	a 2 3	, k = const .
k a3 1	a3 2	a3 3		a3 1	a3 2	a3 3

Это свойство можно сформулировать иначе: умножение всех элементов некоторой строки (столбца) определителя на число k равносильно умножению определителя на это число.

Свойство 5. Если все элементы некоторой строки (столбца) определителя равны нулю, то и определитель равен нулю,

a11	a12	a13	= 0 .
0	0	0	= 0 .
a31	a32	a33

Это свойство вытекает из предыдущего при k = 0 .

Свойство 6. Если элементы двух строк (столбцов) определителя пропорциональны, то определитель равен нулю.

aij :

Свойство 7. Если каждый элемент некоторой строки (столбца) определителя представляет собой сумму двух слагаемых, то такой определитель можно представить в виде суммы двух определителей:

		a/	+a//	a	a		a/	a		a			a//	a		a
		11	11	12	13		11	12		13			11	12		13
Α	=	a/	+a//	a	a	=	a/	a		a		+	a//	a		a		.

		21	21	22	23		21		22		23		21		22		23

		a/	+a//	a	a		a/	a	32	a	33		a//	a	32	a	33
		31	31	32	33		31						31

Свойство 8 . Если к элементам какой-нибудь строки (столбца) определителя прибавить соответствующие элементы другой строки (столбца), умноженные на произвольный множитель k, то величина определителя не изменится:

a11	+k a12	a12	a13		a11	a12	a13
a11	+k a12	a12	a13		a11	a12	a13
a21	+k a22	a22	a23	=	a21	a22	a23	.
a31	+k a32	a32	a33		a31	a32	a33

Замечание: пользуясь свойством 8, можно, не меняя величину определителя, все элементы некоторой строки (столбца) определителя, кроме одного, сделать равными нулю.

Свойство 9 . Определитель произведения матриц равен произведению их определителей.

ОПРЕДЕЛЕНИЕ. Минором Mij элемента aij определителя |A| называется определитель матрицы, полученной из матрицы A вычеркиванием i-й строки и j-го столбца, на пересечении которых стоит элемент aij.

ПРИМЕР: Найдите минор M22 элемента a22 определителя 3-го порядка

a11 a12 a13

A = a21 a22 a23 . a31 a32 a33

Решение: M22 =	a11	a13	.
	a31	a33

ОПРЕДЕЛЕНИЕ. Алгебраическим дополнением Aij элемента aij определи-

теля |A| называется минор Mij этого элемента со знаком (–1)i+j, где i – номер строки, а j – номер столбца, на пересечении которых стоит элемент

				A =		(−1)i + j M		ij .
				ij				ij .
ПРИМЕР:
	1	2	3	: M22 =	1	3	= −12, A22 = (−1)4		M22 = −12 .


Для определителя	4	5	6
	7	8	9		7	9
	7	8	9

ТЕОРЕМА. Определитель численно равен сумме произведений элементов любой его строки (столбца) на соответствующие им алгебраические дополнения

1 / 111 2 3 4 5 6 7 8 9 10 11 > Следующая >>>

Соседние файлы в папке Arkhiv_ZIP_-_WinRAR

#
29.05.20151.95 Mб18Chast_1_Opredeliteli_Matritsy_Sistemy.pdf
#
29.05.20154.52 Mб26Chast_2_Vekt_i_anal_2010_07_29.pdf
#
29.05.20154.89 Mб19Chast_3__Mat_an_2010_23_09.pdf
#
29.05.20151.09 Mб37Chast_5_DifUr.pdf
#
29.05.2015934.06 Кб26Chast_6_FNP.pdf
#
29.05.2015608.76 Кб16Модуль 2_4 Формулы пр.pdf