2012_phys_lp

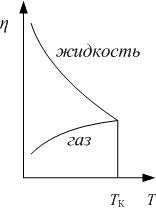
Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.

121

него трения в 1 Н на 1 м2 площади слоев. Эта единица называется паскальсекундой (Па.с). В некоторые формулы (например, число Рейнольдса, формула Пуазейля) входит отношение коэффициента вязкости к плотности жидкости ρ. Это отношение получило название коэффициента кинематической вязкости ν :

Для жидкостей, течение которых подчиняется уравнению Ньютона (16.1), вязкость не зависит от градиента скорости. Такие жидкости называются ньютоновскими. К неньютоновским (то есть не подчиняющимся уравнению (16.1)) жидкостям относятся жидкости, состоящие из сложных и крупных молекул, например, растворы полимеров.

Вязкость данной жидкости сильно зависит от температуры: при изменениях температуры, которые сравнительно нетрудно осуществить на опыте, вязкость некоторых жидкостей может изменяться в миллионы раз. При понижении температуры вязкость некоторых жидкостей настолько возрастает, что жидкость теряет текучесть, превращаясь в аморфное твердое тело.

Я.И. Френкель вывел формулу, связывающую коэффициент вязкости жидкости с температурой:

где А – множитель, который зависит от расстояния между соседними положениями равновесия молекул в жидкости и от частоты колебаний молекул, Е – энергия, которую надо сообщить молекуле жидкости, чтобы она могла перескочить из одного положения равновесия в другое, соседнее (энергия активации). Величина Е обычно имеет порядок (2÷3) .10-20 Дж, поэтому, согласно формуле (16.3), при нагревании жидкости на 100С вязкость её уменьша-

внутреннего трения в жидкостях и газах. Молекулярно-кинетическая теория

объясняет вязкость газов переносом импульса из одного слоя в другой слой, происходящим за счет переноса вещества при хаотическом движении мо-

Вологодский государственный технический университет

Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.

122

лекул газа. В результате в слое газа, движущемся медленно, увеличивается доля быстрых молекул, и его скорость (средняя скорость направленного движения молекул) возрастает. Слой газа, движущийся медленно, увлекается более быстрым слоем, а слой газа, движущийся с большей скоростью, замедляется. С повышением температуры интенсивность хаотического движения молекул газа возрастает, и вязкость газа увеличивается.

Вязкость жидкости имеет другую природу. В силу малой подвижности молекул жидкости перенос импульса из слоя в слой происходит из-за взаимодей-

ствия молекул. Вязкость жидкости в основном определяется силами взаи-

модействия молекул между собой (силами сцепления). С повышением температуры взаимодействие молекул жидкости уменьшается, и вязкость также уменьшается.

Несмотря на различную природу вязкость жидкостей и газов с макроскопической точки зрения описывается одинаковым уравнением (16.1). Величину импульса p , перенесенного из одного слоя газа или жидкости в другой слой за

время t, можно найти из второго закона Ньютона:

Тогда физический смысл коэффициента динамической вязкости можно сформулировать так: коэффициент вязкости численно равен импульсу, пере-

несенному между слоями жидкости или газа единичной площади за единицу времени при единичном градиенте скорости. Знак «минус» показывает,

что импульс переносится из более быстрого слоя в более медленный.

При движении тела в вязкой среде возникают силы сопротивления. Происхождение этого сопротивления двояко.

При небольших скоростях, когда за телом нет вихрей (то есть обтекание тела ламинарное), сила сопротивления обуславливается вязкостью среды. Между движущимся телом и средой существуют силы сцепления, так что непосредственно вблизи поверхности тела слой газа (жидкости) полностью задерживается, как бы прилипая к телу. Он трется о следующий слой, который слегка отстает от тела. Тот, в свою очередь, испытывает силу трения со стороны еще более удаленного слоя и т.д. Совсем далекие от тела слои можно считать покоящимися. Для ламинарного потока сила трения пропорциональна скорости тела: F ~ v . Теоретический расчет внутреннего трения для движения шарика в вязкой среде с небольшой скоростью, когда нет вихрей, приводит к формуле Стокса:

Вологодский государственный технический университет

Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.

ческой вязкости среды.

Второй механизм сил сопротивления включается при больших скоростях движения тела, когда поток становится турбулентным. При увеличении скорости тела вокруг него возникают вихри. Часть работы, совершаемой при движении тела в жидкости или газе, идет на образование вихрей, энергия которых переходит во внутреннюю энергию. При турбулентном потоке в некотором интервале скоростей сила сопротивления пропорциональна квадрату скорости тела: F ~ v2 .

Экспериментальная часть

Приборы и оборудование: лабораторная установка, микрометр, линейка, штангенциркуль, секундомер, шарики.

Методика измерений

Этот метод основан на измерении скорости установившегося движения твердого шарика в вязкой среде под действием постоянной внешней силы, в простейшем случае – силы тяжести.

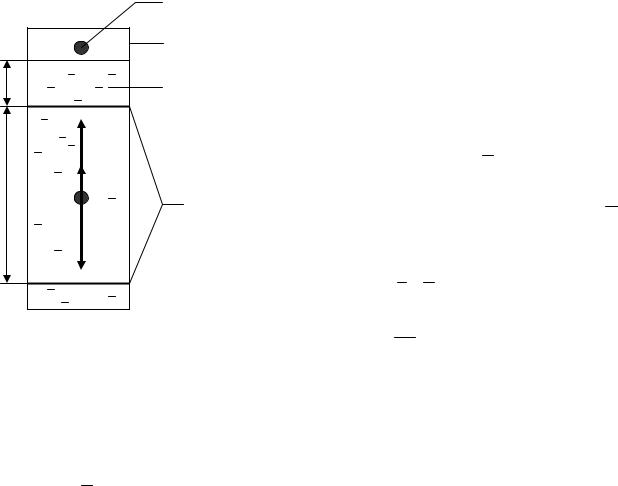
Выведем рабочую формулу для определения коэффициента вязкости методом Стокса. Если взять шарик большей плотности, чем плотность жидкости, то он будет тонуть, опускаясь на дно сосуда. На падающий шарик действуют три силы (рис.16.3):

1.Сила вязкого трения FС по закону Стокса (16.6), направленная вверх, навстречу скорости: Fc = 6 × π ×η × r × v ;

2.Сила тяжести, направленная вниз:

где ρж – плотность жидкости.

Вологодский государственный технический университет

Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.

124

Запишем уравнение движения (второй закон Ньютона) для падающего шарика в проекциях на вертикальную ось:

Сила тяжести и выталкивающая сила не зависят от скорости движения шарика. Сила трения в законе Стокса прямо пропорциональна скорости. Поэтому на некотором начальном участке l0 (рис.16.3) падения шарика в жидкости, пока скорость мала, сила трения меньше разности сил тяжести и выталкивающей, и шарик в результате движется с ускорением. Величину участка l0 можно оце-

нить из уравнения движения.

По мере нарастания скорости падения шарика растет сила вязкого трения. С момента достижения равенства

Далее скорость v шарика выражаем через пройденный путь h и время па-

дения t : v = h : t

Вологодский государственный технический университет

Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.

125

Выведенная формула (16.14) для расчета коэффициента вязкости, как и формула Стокса (16.6), получены в предположении, что шарик движется в сосуде неограниченного объема.

Описание установки

Установка состоит из высокого цилиндрического прозрачного сосуда 1 (рис.16.3), по высоте которого на стенке нанесены на определенном расстоянии друг от друга метки 2. В сосуд налита исследуемая жидкость 3 с известной плотностью (машинное масло или растительное масло). Для определения ее вязкости в верхней части сосуда вблизи центра в жидкость опускают маленькие стальные шарики 4, плотность которых больше плотности жидкости.

Порядок выполнения работы

1.Штангенциркулем измерьте диаметр d шарика.

2.Измерьте линейкой расстояние h между метками.

3.Пинцетом или смоченной палочкой опустите шарик по центру сосуда.

4.Определите при помощи секундомера время t прохождения шарика между метками.

5.Повторите измерения диаметра и времени еще для четырех шариков.

6.Рассчитайте коэффициент вязкости по формуле (16.14) в каждом опыте. Плотности жидкости и шарика возьмите в приложении.

7.Найдите среднее значение коэффициента вязкости.

8.Рассчитайте погрешность η .

9.Сделайте выводы.

Замечание. Погрешность коэффициента вязкости η можно рассчитать

двумя способами:

а) по стандартной методике расчета погрешностей случайной величины:

где коэффициент Стьюдента для числа опытов n = 5 и доверительной вероят-

ности α=0.95 равен: tn, α=2.78; Δηi=|ηср.– ηi|.

б) исходя из формулы (16.14) по стандартной методике расчета погрешностей при косвенных измерениях относительная погрешность равна:

Вологодский государственный технический университет

Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.

Контрольные вопросы

1.Запишите формулу Ньютона для коэффициента динамической вязкости. Сделайте поясняющий рисунок.

2.Что называется коэффициентом динамической вязкости? Поясните его физический смысл и выведите его размерность.

3.Объясните механизм внутреннего трения для газов и жидкостей. Как зависит от температуры вязкость газов и жидкостей? Почему?

4.Какие силы действуют на шарик, падающий в жидкости? Сделайте рисунок, запишите второй закон Ньютона для шарика, падающего в вязкой жидкости.

5.Почему, начиная с некоторого момента, шарик движется равномерно?

6.Как зависит скорость падения шарика от его диаметра?

7.Выведите приближенную расчетную формулу (16.14) для коэффициента вязкости.

Используемая литература

[5] §9.4; [3] §10.7, 10.8; [1] §75, 76, 78, 130; [6] §5.6, 5.7; [7] §31, 33, 48; [10] §16.1; [11] §28.

Вологодский государственный технический университет

Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.

127

Лабораторная работа 1-17 Определение коэффициента вязкости воздуха капиллярным методом

Цель работы: изучение внутреннего трения (вязкости) в газах и определение коэффициента вязкости воздуха.

Теоретическое введение

Газы отличаются от упругих тел тем, что они оказывают сопротивление изменению объема (но не формы). Они всегда оказывают давление, стремясь расшириться и занять любой предоставленный объем.

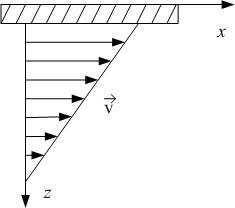
Если газ не находится в состоянии покоя, т.е. равновесие отсутствует, то говорят, что имеется поток газа, и состояние движущегося газа полностью определено, если известна скорость потока в каждой точке пространства в каждый момент времени. Газ рассматриваем как сплошную среду. Для неустановившегося движения газа следует различать два способа описания: вводятся траектории, т.е. пути, описываемые частицами газа с течением времени, и линии тока, которые получаются следующим образом. Представим себе, что в определенный момент в каждой точке потока в виде маленьких стрелок нарисованы векторы скорости частиц. Эти стрелки можно соединить кривыми, касательные к которым в каждой точке направлены вдоль стрелок. В неустановившемся потоке картина линий тока меняется со временем, и траектории частиц газа и линии тока не совпадают. В часто встречающихся на практике задачах рассматривается установившееся движение газа (стационарный поток), когда вектор скорости в каждой точке не меняется со временем, а линии тока совпадают с траекториями частиц. Примером стационарного потока является ламинарное течение. Ламинарным называется поток, в котором газ течет как бы параллельными слоями, скользящими друг относительно друга с различной скоростью. В простейшем случае все слои движутся в одинаковом направлении, например, вдоль оси X . Из-за взаимодействия между слоями (это взаимодействие называется еще внутренним трением) более быстротекущий слой оказывает воздействие на прилегающий к нему слой, пытаясь увлечь его за собой. И наоборот, более медленно текущий слой тормозит более быстрый. Уже Ньютон указал правильный вид этой тормозящей силы: она

должна быть пропорциональна площади S соприкасающихся слоев и спаду скорости в перпендикулярном к потоку направлении. Следовательно, если скорость v x уменьшается в направлении оси z (рис. 17.1), то на каждый слой действует

Вологодский государственный технический университет

Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.

Коэффициент пропорциональности η называется коэффициентом внут-

реннего трения или коэффициентом вязкости.

Ламинарный параллельный поток имеет место, например, при медленном протекании газа в цилиндрической трубе (капилляре) – в этом случае слои представляют собой совокупность бесконечно тонких цилиндрических поверхностей, вложенных одна в другую, имеющих общую ось, совпадающую с осью трубы.

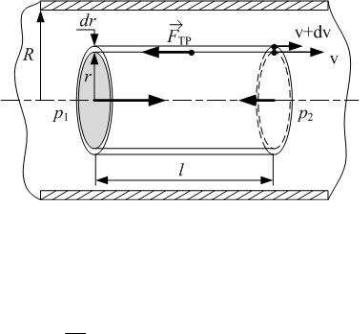
Выделим в капилляре воображаемый цилиндрический объем газа радиусом r и длиной l , как показано на рисунке 17.2. Обозначим давления на его торцах p1 и p2 . При установив-

Сила внутреннего трения определяется по формуле Ньютона (17.1). Учитывая, что S = 2π × r × l (площадь поверхности цилиндра) и скорость v(r ) уменьшается при удалении от оси тру-

бы, т.е. dv < 0 , можно записать: dr

Интегрируя это равенство, получим

v(r ) = - (p1 − p2 )r 2 + C , 4 ×η × l

где C – постоянная интегрирования, которая определяется граничными условиями задачи. При r = R скорость газа должна обратиться в нульv(R) = 0 , по-

Вологодский государственный технический университет

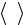
Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.

129

скольку сила внутреннего трения о стенку капилляра тормозит смежный с ней слой газа. Тогда

за единицу времени через поперечное сечение трубы. Через кольцевую пло-

Формулу (17.6), которая называется формулой Пуазейля, можно использовать для экспериментального определения коэффициента вязкости газа.

Формула Пуазейля была получена в предположении ламинарного течения газа или жидкости. Однако с увеличением скорости потока движение становится турбулентным и слои смешиваются. При турбулентном движении скорость в каждой точке меняет свое значение и направление, сохраняется только среднее значение скорости. Характер движения жидкости или газа в трубе определяется числом Рейнольдса:

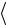где v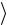 – средняя скорость потока; ρ – плотность жидкости или газа.

Вологодский государственный технический университет

Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.

130

В гладких цилиндрических каналах переход от ламинарного течения к турбулентному происходит при Re » 1000. Поэтому в случае использования формулы Пуазейля необходимо обеспечить выполнение условия Re < 1000 . Кроме этого, эксперимент необходимо проводить таким образом, чтобы сжимаемостью газа можно было пренебречь. Это возможно тогда, когда перепад давлений вдоль капилляра значительно меньше самого давления. В данной установке давление газа несколько больше атмосферного (103см водяного столба), а перепад давлений составляет от ~ 10 см вод.ст., т.е. приблизительно 1% от атмосферного.

Формула (17.6) справедлива для участка трубы, в котором установилось постоянное течение с квадратичным законом распределения скоростей (17.5) по сечению трубы. Такое течение устанавливается на некотором расстоянии от входа в капилляр, поэтому для достижения достаточной точности эксперимента

где ρ – плотность воды. Из (17.6) получим расчётную формулу для динамиче-

ской вязкости:

Вологодский государственный технический университет