2012_phys_lp

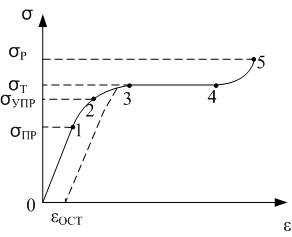
Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.

111

тел, как резина, которые значительно легче поддаются изменению своей формы, чем изменению своего объема.

Таким образом, упругие свойства твердого тела характеризуются двумя величинами: E и μ .

Отметим, что в наших рассуждениях мы подразумеваем, что твердое вещество изотропно – свойства его одинаковы во всех направлениях. Упругие свойства анизотропных тел – монокристаллов – характеризуются большим числом упругих постоянных (не 2, а 21 – в самом общем случае).

Упругие деформации, по определению, исчезают после снятия вызывающих их напряжений (абсолютно упругое тело). Конечно, реальные твердые тела вовсе не обладают этой способностью в полной мере. Только пока деформации тела не превосходят известных пределов, оно восстанавливает свою форму, и то лишь с известной степенью точности. Минимальное механическое напряжение, при котором реальные тела ведут себя приблизительно как тела абсолютно упругие, называется пределом упругости. Различные тела обладают различным пределом упругости, но для всех тел существует такое напряжение, что после снятия нагрузки тело уже не возвращается к исходному состоянию и сохраняет в заметной степени измененную форму. Такие деформации называются остаточными или пластическими.

Рассматривать тела как абсолютно упругие имеет смысл только при условии, что деформации тел заведомо не достигают предела упругости. При малых и медленных деформациях многие реальные твердые тела можно считать абсолютно упругими. Вопрос о том, как малы и медленны должны быть деформации, чтобы данное реальное тело можно было рассматривать как абсолютно упругое, должен быть решен на опыте путем изучения поведения тел при различных величинах деформаций.

Для этой цели применяются специальные машины, в которых образцы испытуемого материала подвергаются различным деформациям. Результаты испытаний материалов представляют в виде графиков, изображающих связь между деформациями образца и напряжениями (силами), в нем возникающими (рис.14.2). Как видно из рисунка 14.2, при малых

деформациях напряжение пропорционально деформации: σ ~ ε (участок 0-1). Это область пропорциональности. Максимальное напряжение, при котором выполняется закон Гука, называется пределом пропорциональности. Далее напряжения растут медленнее, чем деформации (1-3 на рис.14.2). В этой области

Вологодский государственный технический университет

Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.

112

и лежит предел упругости тела. Точного определения предела упругости дать вообще невозможно, так как малые остаточные деформации наблюдаются всегда. Пределом упругости можно считать такое наибольшее механическое напряжение, после снятия которого остаточные деформации невелики (они не превышают некоторой определенной условно выбранной доли от наибольшей деформации, которой подвергается образец, например, 0.001%). Предел упру-

гости σ лежит обычно близко за пределом пропорциональности σ . Дальше

У ПР

начинается область текучести (участок 3-4 на рис.14.2). Под действием напряжения, равного пределу текучести σ т , тело непрерывно увеличивает свою де-

формацию без увеличения нагрузки; оно будет течь как жидкость. При еще

больших деформациях наступает разрушение (точка 5). Предел прочности σ –

Р

минимальное напряжение, при котором начинается разрушение тела.

Область упругих деформаций в большинстве применяемых на практике материалов очень незначительна (например, для стали пределу упругости соответствует значение ε ≈ 0.01). Поэтому наибольшие деформации, которые может выдержать данный материал без разрушения, определяются главным образом величиной области текучести. Материалы, для которых эта область мала, способны выдерживать без разрушения только малые деформации – это хрупкие материалы. Те же, которые способны без разрушения выдерживать большие деформации – вязкие материалы. Например, чугун и сталь имеют примерно одинаковую область упругих деформаций и примерно одинаково ведут себя в этой области – они в одинаковой степени упругие. Но область текучести у чугуна гораздо меньше, чем у стали, поэтому он гораздо более хрупок.

Экспериментальная часть

Приборы и оборудование: лабораторная установка, набор грузов (гирь).

Лабораторная установка и методика измерений

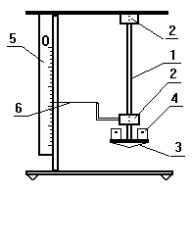
Установка для измерения схематически показана на рис. 14.3. Исследуемый образец (резиновый шнур) 1 имеет на концах металлические зажимы 2. Верхний зажим закреплен неподвижно к штативу, к нижнему зажиму подвешена платформа 3 для размещения гирь 4. Параллельно образцу закреплена линейка 5. На шкале линейки 5 находится стрелка 6, основание которой закреплено на нижнем зажиме. При растяжении образца стрелка перемещается на величину абсолютного удлинения.

Рис. 14.3

В нашем опыте роль внешней силы F играет

Вологодский государственный технический университет

Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.

Порядок выполнения работы

1.При свободной от гирь платформе штангенциркулем измерьте диаметр ненагруженного образца d0 . Следите, чтобы штангенциркуль не зажимал ре-

зину, а лишь только касался ее поверхности. Результаты всех измерений и вычислений записывайте в таблицу 14.1.

Таблица 14.1

Вологодский государственный технический университет

Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.

114

2.По шкале линейки найдите длину ненагруженного образца l0 . За концы об-

разца можно принимать внутренние концы зажимов. Оцените погрешность этой величины δ l0 .

3.Найдите начальное положение стрелки x0 . Положение стрелки отмечают с

точностью 0.5 мм, то есть погрешность измерения удлинения равна x = δ ( l ) = 0.0005 м .

4.Ставьте на платформу грузы парами (симметрично подвесу во избежание

перекоса). Каждый раз отмечайте показания стрелки x . Вычислите удлинения l = x − x0 .

5.При максимальной нагрузке штангенциркулем измерьте диаметр образца d .

6.Для проверки применимости закона Гука постройте графики зависимости модуля Юнга E от напряжений σ .

ляют определить истинное (среднее) значение модуля Юнга. С учетом этого определите среднее значение модуля Юнга.

9.Определите значение коэффициента Пуассона.

10.Сделайте выводы.

Замечание: относительная погрешность модуля Юнга может быть рассчитана по формуле:

Контрольные вопросы

1.Что такое модуль Юнга? От чего он зависит?

2.Как связаны жёсткость и модуль Юнга?

3.Что такое абсолютное и относительное удлинение образца?

4.Что такое механическое напряжение?

5.Что такое коэффициент Пуассона?

6.Что такое абсолютное и относительное поперечное сжатие?

7.Какие из перечисленных характеристик относятся к материалу?

8.Какие из перечисленных характеристик относятся к образцу?

9.Сформулируйте закон Гука.

Вологодский государственный технический университет

Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.

115

10.Нарисуйте кривую зависимости σ (ε ) и расскажите о ее характерных точках и участках.

11.Что такое деформация сдвига?

12.Что такое пластическая деформация? Поясните рисунком на примере деформации сдвига.

13.В чем состоит суть данного метода измерения модуля ЮнгаE ?

14.Какие размерности у E и μ ?

15.Каков порядок величин E для различных твердых тел?

16.Учитывается ли в опыте масса самого образца?

17.Почему в лабораторной работе используется резиновый образец, а, например, не стальной?

Используемая литература

[1] §14; [7] §21; [4] §48; [10] §29.

Лабораторная работа 1-15 Определение модуля Юнга методом прогиба

Цель работы: определение модуля Юнга материала путем измерения прогиба образца при нагрузке.

Теоретическое введение

Внимание! Перед выполнением работы 1-15 рекомендуется прочитать теоретическое введение к лабораторной работе 1-14.

Прочность, долговечность и надежность металлических изделий (твердых тел), работающих в различных условиях, во многом зависит от характеристик, определяющих упругие свойства материалов. Твердые тела при этом будем рассматривать как сплошную среду с определенной плотностью ρ . Под воздействием внешних сил твердые тела в той или иной степени деформируются, то есть изменяют свою форму и объем. При всем разнообразии деформаций тел любую деформацию можно свести к двум основным (элементарным): растяжению (сжатию) и сдвигу.

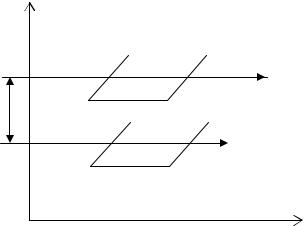
Сдвигом называется такая деформация твердого тела, при которой все его плоские слои, параллельные некоторой неподвижной плоскости, называемой плоскостью сдвига, не искривляясь и не изменяясь в размерах, смещаются па-

Вологодский государственный технический университет

Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.

116

где F|| – сила, параллельная поверхности твердого тела площадью S и вызы-

вающая сдвиг. При малых деформациях закон Гука в этом случае имеет вид, аналогичный (14.3):

лом сдвига γ – называется модулем сдвига. Итак, упругие свойства деформируемого упругого тела характеризуются двумя основными модулями упругости

– модулем Юнга E и модулем сдвига G . Еще одна упругая константа – коэффициент Пуассона μ . В изотропных твердых телах (у таких тел свойства оди-

наковы во всех направлениях) эти три константы E , G и μ не являются независимыми, а связаны между собой соотношением

Из (15.3) следует, что в твердых телах G < E .

Экспериментальная установка и методика измерений

В работе определяется модуль Юнга предложенных образцов и проверяется зависимость деформации от нагрузки. Используется установка, которая показана на рис. 15.2 и 15.3. На исследуемый образец надевается подвеска для

Рис. 15.2

Вологодский государственный технический университет

Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.

117

грузов, а образец кладется на острые металлические опоры. Подвеска с грузами находится на одинаковом расстоянии от точек опоры стержня. Стрела прогиба h образца измеряется индикатором часового типа. Изгиб представляет собой более сложный вид деформации, чем деформация растяжения или сжатия. Нижние слои стержня при этом испытывают деформацию растяжения, верхние

– деформацию сжатия, а средний слой, длина которого не изменяется, нагрузок не несет и называется нейтральным. При так называемом чистом изгибе напряжения, которые испытывают слои материала при деформации, имеют прямую зависимость от их деформации: сжатию соответствуют отрицательные напряжения, растяжению – положительные.

Величина прогиба h при этом оказывается прямо пропорциональной нагрузке F , а коэффициент пропорциональности зависит от модуля Юнга образ-

ца E : h ~ F , где F = mg . Вывод формулы для модуля Юнга по этому методу

E

относительно сложен. Окончательно формула имеет вид:

рина образца, b – толщина образца.

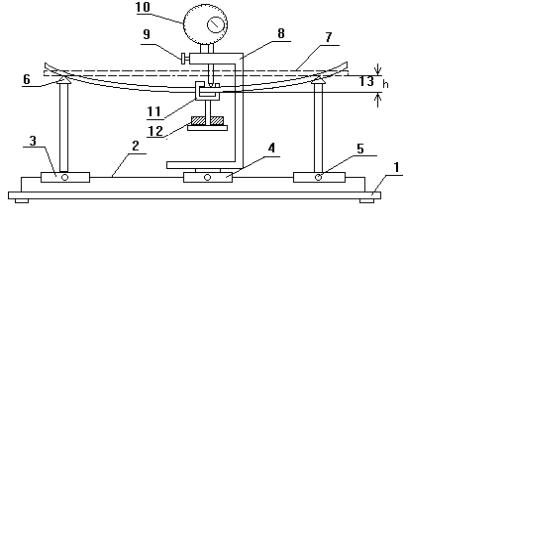
Схема установки для определения модуля Юнга по прогибу представлена на рис. 15.3. На основании 1 закреплена массивная направляющая 2. По ней могут перемещаться стойки 3 и кронштейн 4, зажимаемые в необходимом положении винтами 5 (вручную).

Стойки вверху оканчиваются призмами 6, на параллельные острия которых устанавливается измеряемый образец 7. В гнезде 8 кронштейна зажимается вручную винтом 9 индикатор перемещения 10. На образце напротив индикатора подвешена серьга 11 с платформой для специальных (с прорезью) гирь 12. При нагружении платформы гирями образец прогибается. Стрела прогиба 13 регистрируется перемещением стрелки индикатора.

Рис. 15.3

Вологодский государственный технический университет

Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.

118

Порядок выполнения работы

1.Ослабив винты 5, установите призмы 6 на заданное (преподавателем) расстояние. Закрепите винты.

2.Установите кронштейн 4 на одинаковом расстоянии от стоек. Закрепите винты.

3.Расположите образец на призмах так, чтобы гнездо индикатора находилось над средней частью по ширине образца.

4.Вставьте индикатор в гнездо, осторожно утопив его так, чтобы стрелка малой шкалы оказалась около метки 5 мм. Аккуратно зажмите индикатор винтом 9.

5.Измерьте штангенциркулем толщину b и ширину a образца.

6.Все результаты заносите в таблицу 15.1.

7.Измерьте линейкой расстояние между ребрами призм l.

8.Установите поворотом кольца нуль на индикаторе. Определите цену деления индикатора.

9.Аккуратно поставьте на платформу гирю массой m. Определите стрелу прогиба h по красной шкале индикатора.

10.Снимите с платформы гирю. Если стрелка сместилась с нулевой отметки, установите нуль. Повторите для контроля несколько раз измерения с тем же грузом.

11.Проведите аналогично пункту 9 измерения прогиба с гирями большей массы.

12.Рассчитайте модуль Юнга при каждом измерении и усредните результат.

13. Рассчитайте ошибку определения модуля Юнга E (достаточно рассчитать для одного опыта).

Вологодский государственный технический университет

Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.

рабочей формулы (15.4):

Контрольные вопросы

1.Что такое модуль Юнга?

2.Что такое абсолютное и относительное удлинение образца?

3.Что такое механическое напряжение?

4.Что такое коэффициент Пуассона?

5.Что такое абсолютное и относительное поперечное сжатие?

6.Какие из перечисленных характеристик относятся к материалу?

7.Какие из перечисленных характеристик относятся к образцу?

8.Сформулируйте закон Гука для деформации сжатия (растяжения).

9.Нарисуйте кривую зависимости σ (ε ) и расскажите о ее характерных точках

иучастках.

10.Что такое деформация сдвига? Сформулируйте закон Гука для деформации сдвига.

11.Что такое пластическая деформация? Поясните рисунком на примере деформации сдвига.

12.В чем состоит суть данного метода измерения Е?

13.Зависит ли модуль Юнга от нагрузки и стрелы прогиба?

14.Чем отличается деформация прогиба от деформации растяжения?

Используемая литература

[1] §14; [7] §21; [4] §48; [10] §2.9.

Вологодский государственный технический университет

Физические основы механики, физика колебаний и волн, термодинамика: лабораторный практикум / под ред. Богданова В.И.

120

Лабораторная работа 1-16 Определение коэффициента вязкости жидкости методом Стокса

Цель работы: ознакомление с методом Стокса и определение коэффициента вязкости различных жидкостей.

Теоретическое введение

Во всех реальных жидкостях и газах при перемещении одного слоя относительно другого возникают силы трения. Со стороны слоя, движущегося более быстро, на слой, движущийся медленнее, действует ускоряющая сила. Наоборот, со стороны слоя, движущегося медленнее, на более быстрый слой действует тормозящая сила. Эти силы, носящие название сил внутреннего трения, на-

щей между слоями, пропорциональна площади соприкосновения движущихся слоёв и градиенту скорости (закон Ньютона):

что сила направлена противоположно градиенту скорости, то есть быстрый слой тормозится, а медленный – ускоряется .

Единицей измерения коэффициента вязкости в СИ служит такая вязкость, при которой градиент скорости, равный 1 м/с на 1м, приводит к силе внутрен-

Вологодский государственный технический университет