2.2. Случайная погрешность

Наличие случайных погрешностей в результате при повторении изме- рений в неизменных условиях эксперимента объясняется самой природой этих погрешностей. Строго говоря, условия не остаются неизменными и их колебания вызывают непостоянство результата, т.е. случайные погрешности всегда будут присутствовать в результате измерений.

Характером проявления случайной погрешности определяется и способ их учета. Учесть влияние случайных погрешностей на результат измерения можно только путем анализа всей совокупности случайных погрешностей.

Случайная погрешность считается случайной величиной, и поэтому ее оценивают методами математической статистики и теории вероятности. Наи- более полной характеристикой случайной погрешности является закон рас- пределения, представляющий собой зависимость вероятности появления случайной погрешности от величины этой погрешности. Большинство ре- зультатов измерений содержит случайную погрешность, подчиняющуюся нормальному закону распределения:

x

1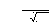

x_i

2

_{W е} ²

2

_{, (2.5)}

2

x

x

i

где W( ) – плотность вероятности случайной погрешности отдельного измерения _i , это отклонение может быть вычислено для каждого измерения. Следует помнить, что сумма отклонений ре- зультата измерений от среднего значения равна нулю, а сумма их квадратов минимальна. Эти свойства используются при обработке результатов измерений для контроля правильности вычислений;

– параметр, характеризующий степень случайного разброса ре- зультатов отдельных измерений относительно истинного значения Х₀, называют средним квадратическим отклонением случайной ве- личины измерения;

Х ^{- математическое ожидание результатов наблюдений.}

Х ^{, – являются точечными оценками случайной погрешности.}

При случайных погрешностях результат каждого измерения Х_i будет отличаться от истинного значения Х₀ измеряемой величины:

_(2.6)

Х _i X ₀

Эту разность называют случайной погрешностью отдельного измере- ния (результата наблюдения).

Истинное значение Х₀ неизвестно, поэтому на практике его заменяют наиболее достоверным значением измеряемой величины, определяемым на основании экспериментальных данных.

Если проводить серию измерений исследуемой величины и определить среднее арифметическое значение, то оно является наиболее достоверным значением измеряемой величины. При вычислении среднего арифметическо- го большого числа измерений погрешности отдельных измерений, имеющие разный знак, взаимно компенсируются.

_{Среднее арифметическое значение принимают за результат измерения:}

i

_Х Х ₁ Х ₂

^Х 3 ^{ Х} n i 1

n

Х

_{n n}

(2.7)

где x_i – численный результат отдельного измерения;

n – число измерений.

В теории случайных погрешностей вводится понятие о среднем квадратическом отклонении результата отдельного измерения (средняя квадратическая погрешность результата наблюдения)

(

n