--II семестр-- / Лекции1 / Лекция 8

Лекция 8

Алгоритмы, использующие

непрерывно – дискретные методы оптимизации.

При использовании данных методов оптимизации задача размещения решается в два этапа:

• на первом этапе определяют координаты место­положения центров элементов, при которых целевая функция F имеет экстремальное значение;

• на втором - полученные координаты "округляют­ся" в фиксированные целочисленные значения координатной сетки, нане­сенной на поверхность коммутационной платы,

Алгоритмы, использующие градиентные методы.

При использовании градиентных методов для отыскания оптимального размещения элементов на плате по критерию минимума суммарной взвешен­ной длины соединений решение задачи сводится к минимизации целевой функции

где (x_i,y_j) и (x_j,y_j)- координаты I-ой и j-ой позиции коммутационной платы;

с_ij -весовые оценки связей.

При ограничениях:

x* x_i a-x* для 1 i q;

x_i=x* для q+1 i h;

y*y_i b-y* для 1 i h;

x _i _i; y_i =_i для h+1 i n.

где x* и y* - координаты центра левой нижней позиции; _i и _i - координаты центра i-го фиксированного элемента. Так как целевая функция является многомерной, то градиент аналити­чески выражают в виде суммы частных производных по всем нефиксирован­ным координатам x_i (i=1,2,3…,q) и y_i(i=1,2,3,…,h)

где - орты (qh) – мерного пространства.

Движение по координатам x_i и y_i осуществляют до тех пор, пока на очередной итерации не будут выполняться соотношения:

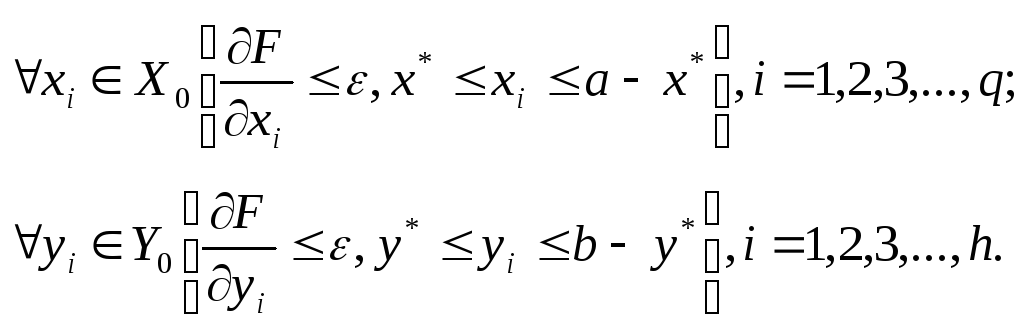
где - ранее заданная погрешность нахождения экстремума F.

При использовании градиентных методов местоположение конструк­тивных элементов на плате получается в непрерывных координатах. Поэ­тому на втором этапе проводят "округление" полученных величин до ближайших целочисленных координат, т.е. все нефиксированные элементы сдвигаются в фиксированные позиции координатной сетки платы. При этом для оценки оптимальности сдвига используют критерий минимума суммы квадратов приращения координат:

где (x_i, y_i) и (A_i,B_i) - координаты центра i -го элемента и i -ой позиции соответственно.

К достоинствам градиентных методов относятся сравнительно небольшие затраты времени на отыскание экстремума целевой функции, а также наличие стандартных программ для решения данного класса задач. Недостатками этой группы алгоритмов являются:

• возмож­ность получения лишь локального экстремума;

• большая неравномерность распределения элементов на плате до "округления" координат.

В связи с указанными недостатками в чистом виде градиентные мето­ды для решения задач размещения не используют. Их применяют в сочета­нии с методами случайного поиска, отыскивая при этом глобальный экст­ремум целевой функции.

Алгоритмы, использующие динамические модели.

В основу этой группы алгоритмов положен динамический метод B.C. Линского. Процесс размещения элементов на плате представляется как движение к состоянию равновесия системы материальных точек (эле­ментов), на каждую из которых действуют силы притяжения и отталкива­ния, интерпретирующие связи между размещаемыми элементами. Если силы притяжения, действующие между любыми двумя материальными точками r_i и r_j. пропорциональны числу электрических связей между данными конструктивными элементами, то состояние равновесия такой системы со­ответствует минимуму суммарной длины всех соединений. Введение сил отталкивания материальных точек друг от друга и от границ платы исключает возможность слияния двух любых точек и способствует их равномерному распределению по поверхности монтажного поля. Чтобы устранить возникновение в системе незатухающих колебаний, вводят силы сопротивления среды, пропорциональные скорости движения мате­риальных точек. Задача оптимального размещения элементов сводится к нахождению такого местоположения точек, при котором равнодействующие всех сил обращаются в нуль. Решение задачи осуществляется в три этапа. На первом этапе, используя критерий минимума суммарной взвешенной длины связей, производят размещение материальных точек на условном поле позиций без учета требовании равномерности их распределения по по­верхности и попадания точек в фиксированные позиции поля. Полученное решение используют в качестве начального размещения на вто­ром этапе, где на материальные точки начинают действовать силы при­тяжения и отталкивания. Под влиянием этих сил точки начинают переме­щаться к положению равновесия системы, при котором обеспечивается при­емлемая степень равномерности их размещения на поле позиций. На третьем этапе точки сдвигаются в фиксированные позиции платы при минимально возможных изменениях их взаиморасположения.

Рассмотрим отдельные этапы работы данного алгоритма. Пусть необ­ходимо минимизировать целевую функцию (1) при ограничениях (2). Для получения начального размещения точек приравняем все частные производные по нефиксированным координатам нулю и решим систему (q+h) линейных уравнений:

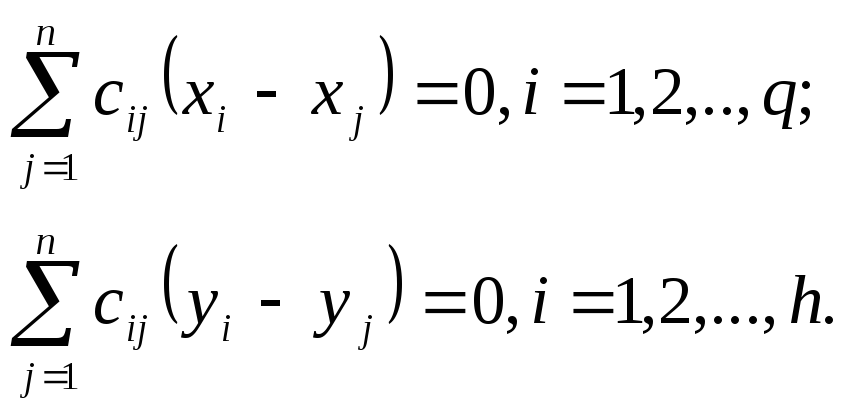
Однозначное решение может быть получено лишь при наличии в каждой связной компоненте не менее двух фиксированных точек (каждое урав­нение должно иметь не менее двух данных значений координат). Если какая-либо связная компонента имеет только одну фиксированную точку, то в результате минимизации длины связей все точки этой компоненты сольются с фиксированной. Отсутствие фиксированных точек в любой связной компоненте приведет не только к слиянию всех ее точек, но и к неопределенности ее местоположения. Как правило» одна из таких фиксированных точек имеется в каждой цепи на разъеме, другую фикси­руют искусственно, причем желательно, чтобы ее местоположение было как можно дальше от разъема.

Затем рассматривают движение материальных точек из полученного первоначального размещения к положению равновесия системы. Для каждой пары точек r_i и r_j вводят силы притяжения:

и отталкивания:

Кроме того, к каждой точке r_i прикладывают силы отталкивания от границ платы:

и сопротивления среды:

,

где k - некоторый положительный коэффициент;

- скорость движения i -ой точки.

Движение нефиксированных материальных точек описывается системой дифференциальных уравнений:

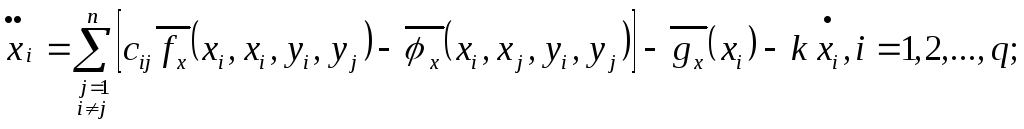
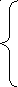
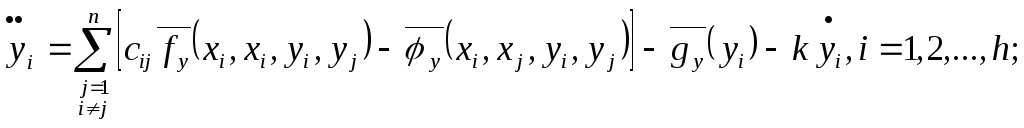
Для решения данной системы уравнений можно использовать метод Эйлера, который позволяет выполнить последовательные вычисления значений произвольной функции:

по уравнению

;

где h (z^(t),x^(t)) - значения на t -oм шаге;

х^(t) ,х^(t+1),z^(t),z^(t+1) - значения аргументов и искомой функции на t-ом и на (t+1) -ом шагах соответственно.

Выражения для сил, действующих на материальные точки, определя­ются разработчиком, исходя из требований к размещению элементов на плате. В качестве примера рассмотрим один из возможных вариантов этих выражений.

Силы притяжения:

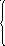
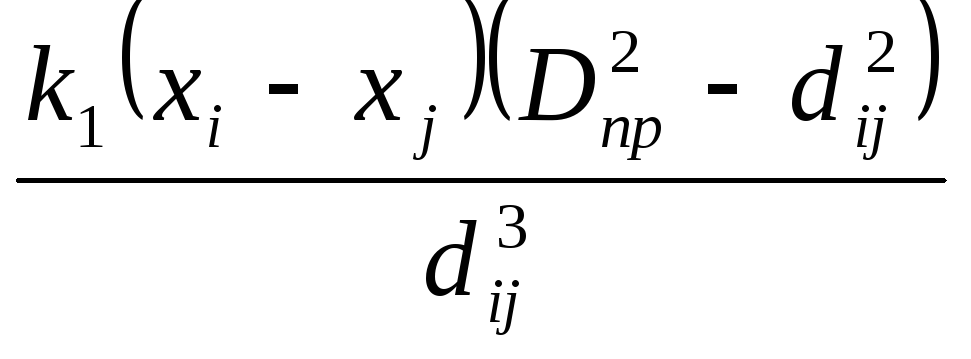, если ;

0 – в противном случае

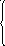
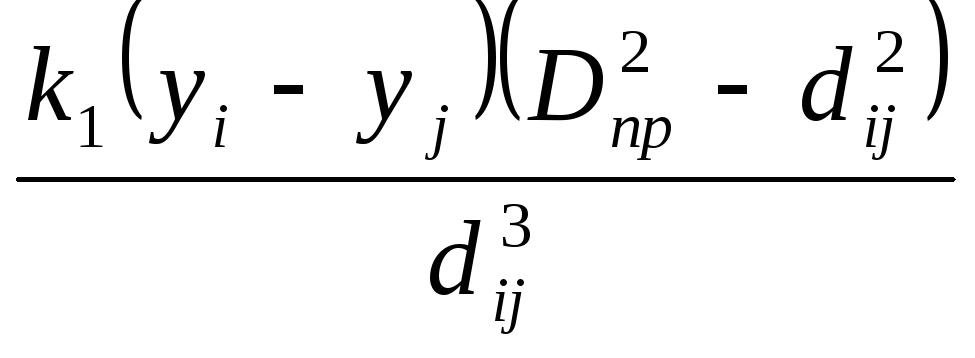, если ;

0 – в противном случае

где k₁ - коэффициент пропорциональности;

;

D_np - коэффициент, учитывающий диапазон действия сил притяжения.

Силы отталкивания точек друг от друга:

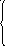
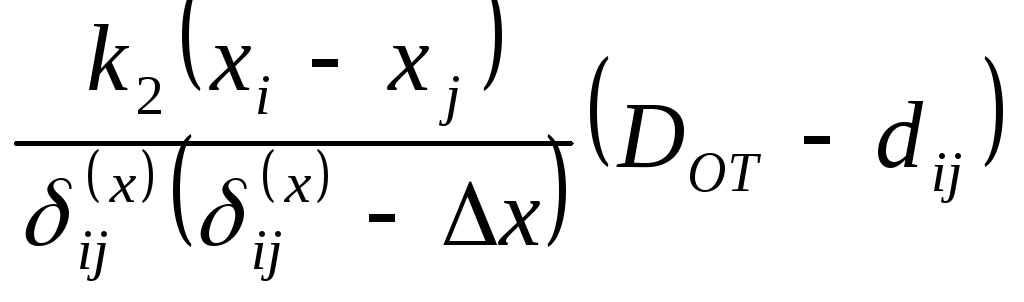, если ;

0 – в противном случае

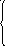
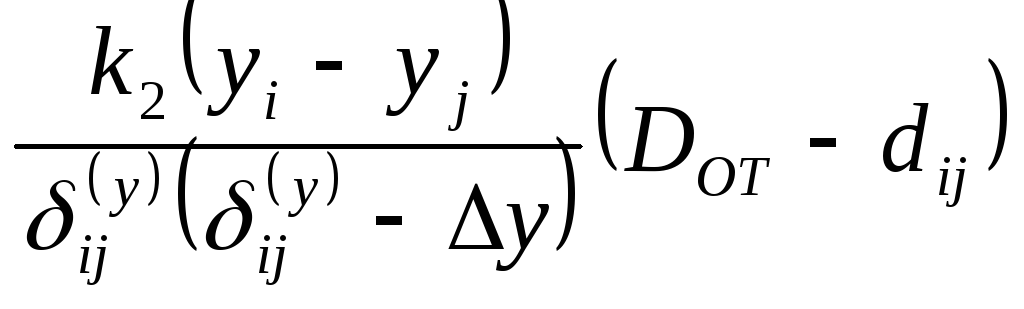, если ;

0 – в противном случае

где k₂- коэффициент пропорциональности;

;

;

x, y- величины возможного сближения конструктивных элементов по осям X и Y ;

D_OT - коэффициент, учитывающий диапазон действия сил отталкивания.

Силы отталкивания от границ платы:

;

,

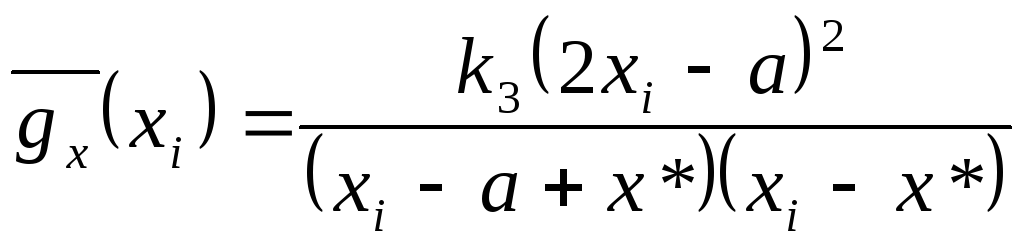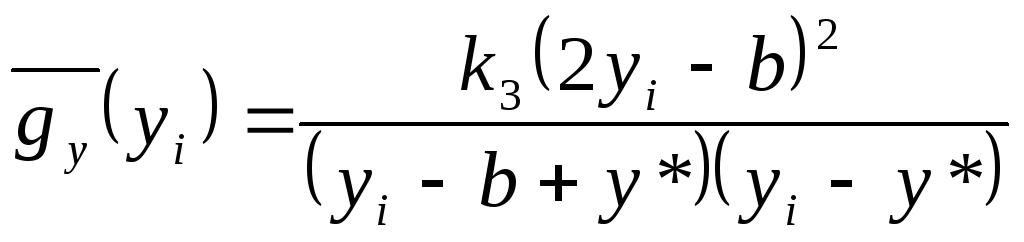где k₃ - коэффициент пропорциональности.

Вычисления продолжаются до тех пор, пока будет выполняться ус­ловие:

где  - допустимая погрешность нахождения оптимального решения.

"Округление" полученных координат производят до ближайших цело­численных величин, соответствующих фиксированным позициям монтажно­го поля. Для оценки оптимальности сдвига элементов используют кри­терий, что и в градиентных методах.

Достоинства метода:

• возможность получения глобального экстремума целевой функции,

• сведение поиска к вычислительным процедурам, для которых имеются разработанные численные методы.

Недостатки:

• тру­доемкость метода и сложность его реализации /подбора коэффициентов для силовых связей;

• необходимость фиксирования местоположения некото­рого числа конструктивных элементов на плате для предотвращения боль­шой неравномерности их размещения на отдельных участках платы.

Данный метод целесообразно использовать в тех случаях, когда позиции для установки элементов на коммутационной плате заранее не фиксированы, что имеет место при размещении разногабаритных элемен­тов

41