
--II семестр-- / Лекции1 / Лекция 4
.docЛекция 4.
Алгоритмы покрытия.
В основе построения большинства алгоритмом покрытия используется идея выделения из заданной функциональной схемы подсхем (групп максимально связанных между собой логических элементов), перебора всех или достаточно большого их числа и проверки на совпадение логических функций элементов подсхем и компонентов модулей, используемого набора. Подсхема закрепляется затем модулем, в состав которого входит наибольшее количество ее логических функций. Процесс продолжается до полного распределения элементов функциональной схемы по модулям.
Рассмотрим эвристический алгоритм, являющийся типичным для приближенных алгоритмов покрытия, используемых в системах проектирования РЭА. Исходная функциональная схема представляется множеством связанных между собой логических элементов
М={m1,m2,…,mn},
каждый
из которых
![]() реализует
некоторую функцию
реализует
некоторую функцию
![]() (И,
ИЛИ, НЕ, исключающее ИЛИ, запоминание и
т.д.) а их множество М определяет
совокупность всех логических операций
выполняемых
в схеме.
(И,
ИЛИ, НЕ, исключающее ИЛИ, запоминание и
т.д.) а их множество М определяет
совокупность всех логических операций
выполняемых
в схеме.
=U i = {1, 2,…, n}
Имеется ограниченный набор типов модулей
N={n1,n2,…,ne},
на
базе которого необходимо выполнить
заданную схему. Каждый модуль
![]() реализует одну или несколько логических
операций
реализует одну или несколько логических
операций
![]() ,
,
а полный набор модулей N определяет совокупность всех логических операций
j
=Uj
j
={![]() ,
,![]() ,
,![]() },
},
которые могут быть получены с их помощью.
При этом могут иметь место два случая:
-
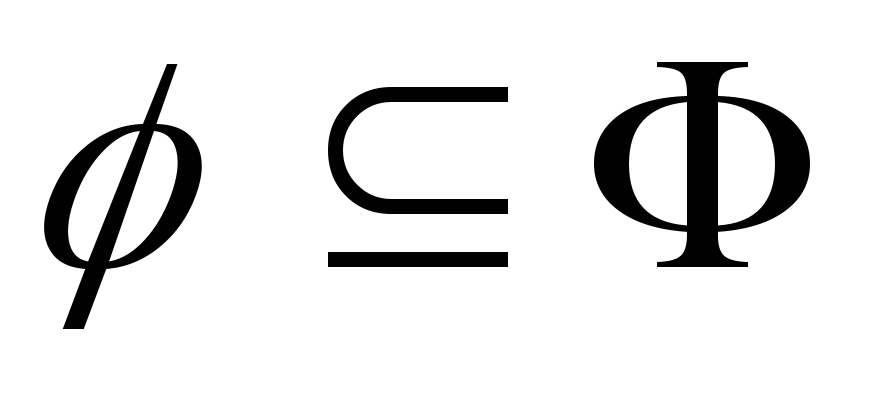 ,
т.е. для каждого элемента функциональной
схемы существует соответствующий
аналог среди компонентов набора модулей;
,
т.е. для каждого элемента функциональной
схемы существует соответствующий
аналог среди компонентов набора модулей; -
 ,
т.е. компоненты набора модулей реализуют
не все функциональные схемы.
,
т.е. компоненты набора модулей реализуют
не все функциональные схемы.
В
первом случае, функциональную схему
устройства можно полностью покрыть
модулями заданного набора, во втором –
требуется доработка покрытия, связанная
с подбором дополнительных модулей,
позволяющих покрыть элементы из
подмножества
![]() ,
выполняющие операцию \Ф,
при этом процесс покрытия схемы
разбивается на два этапа:
,
выполняющие операцию \Ф,
при этом процесс покрытия схемы
разбивается на два этапа:
-
предварительный
-
окончательный
Алгоритм предварительного покрытия работает следующим образом:
-
Из списка элементов схемы, подлежащих покрытию, выбирают очередной элемент
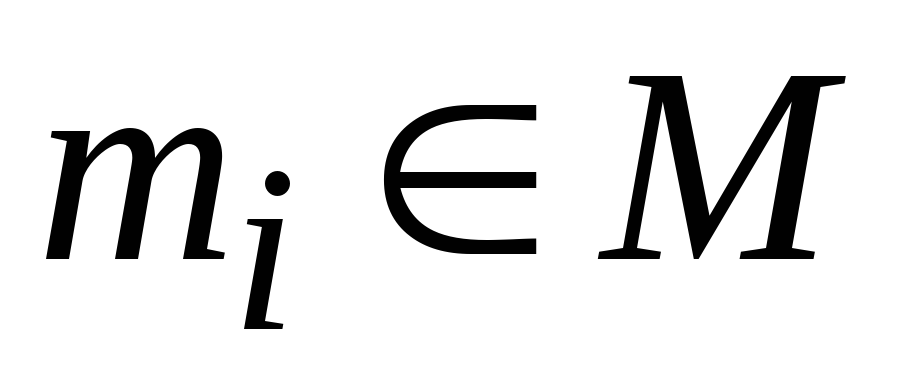 .
Если список пуст, то переходим к пункту
8.
.
Если список пуст, то переходим к пункту
8. -
Определяем все логические элементы
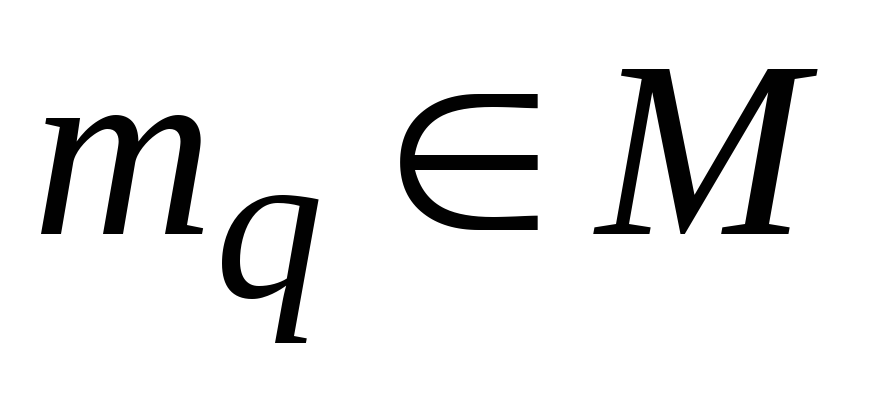 из
числа непокрытых, связанные с mi
и формируем множество Мi
=
mi
U
mq.
из
числа непокрытых, связанные с mi
и формируем множество Мi
=
mi
U
mq. -
Производим сравнение функции h, реализуемых в каждой из конструктивных модулей
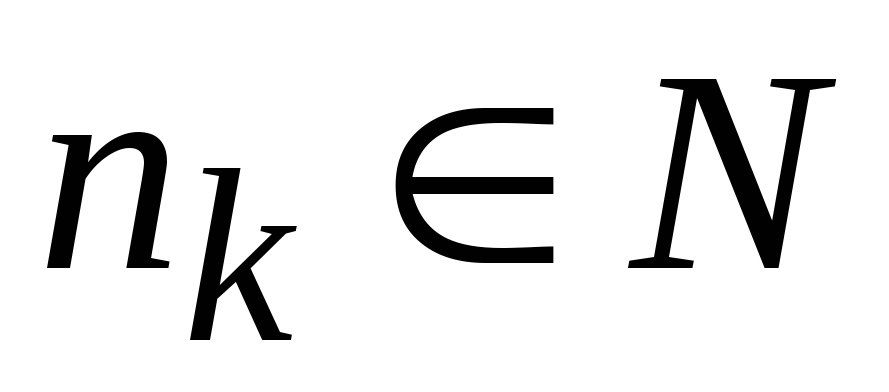 и
логических функций
и
логических функций
![]() .
.
Выбираем
модуль
![]() ,
для которого
,
для которого
i ∩q = max[i ∩h],
если таких модулей несколько, то выбираем модуль наименьшей стоимости. Если при пересечении этих множеств образуется пустое множество i ∩q = 0, то переходим к пункту 7.
-
Если эти множества равны (i ∩q), то переходим к пункту 6.
-
Из Mi удаляем элементы
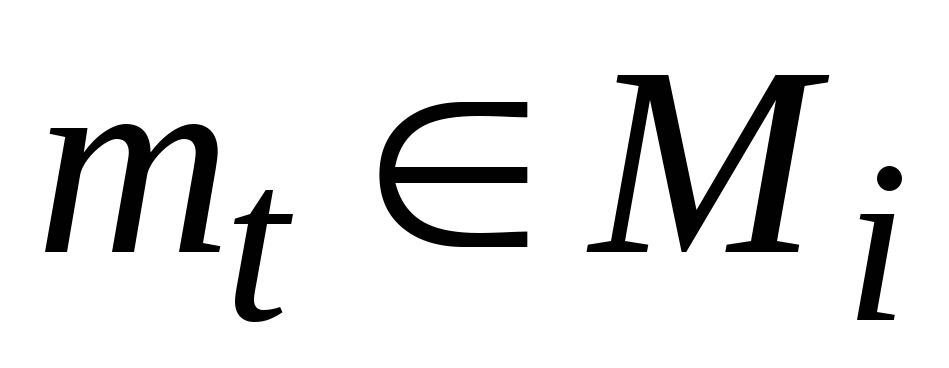 ,
наименее связанные с оставшимися и
выполняющие операции i
\
q
.
Получаем множество элементов
,
наименее связанные с оставшимися и
выполняющие операции i
\
q
.
Получаем множество элементов
 ,
которые целесообразно скомпоновать в
едином корпусе nq.
,
которые целесообразно скомпоновать в
едином корпусе nq. -
Закрепляем все выбранные логические элементы за модулем nq и переходим к пункту 1.
-
Составляем список элементов функциональной схемы, которые не могут быть реализованы с помощью заданного набора модулей (требуется доработка). Переходим к пункту 1.
-
Конец работы алгоритма.
Для улучшения полученного результата осуществляют парные перестановки однотипных логических элементов различных модулей.

