теория

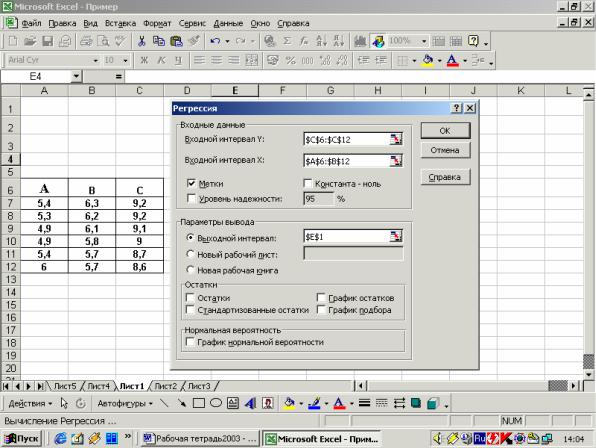
Вычисление параметров линейного уравнения парной регрессии проводится с помощью инструмента анализа данных Регрессия. Порядок действий следующий: в главном меню последовательно выберите пункты Сервис/Анализ данных/Регрессия, после чего щелкните по кнопке Ок.

Заполните диалоговое окно ввода данных и параметров вывода.

Результаты множественного регрессионного анализа представлены ниже:

Согласно расчетам, полученным в Excel, зависимость доходов по акции С от доходов по акциям А и В имеет вид:

что означает, что при увеличении доходов по акции А на 1% доходы по акции С уменьшатся на 0,24%, а при увеличении доходов по акции B на 1% доходы по акции С увеличатся на 0,77%.

Оценка тесноты связи дает следующие результаты:

R ≈ 0.98 , R 2 ≈ 0.96 ,

т.е. связь между доходами по акции С и доходами по акциям А и В сильная и 96% изменения доходов по акции С объясняется изменением доходов по акциям А и В.

Уравнение значимо на 5% уровне, т.к. значение «значимость F» меньше 0,05. Кроме того, на 6% уровне значимы оба коэффициента, ошибка первого коэффициента чуть больше 5%, а у второго – меньше 1%. Доверительный

интервал для коэффициента a 2 можно проинтерпретировать так: при увеличении доходов по акции В на 1% доходы по акции с увеличатся на величину от 0,41% до 1,14%.

Таким образом, нами продемонстрирован один из многочисленных инструментов анализа данных, имеющихся в ППП MS Excel. Ознакомиться с другими инструментами можно самостоятельно.

Практика построения множественных регрессионных моделей взаимосвязи показывает, что реально существующие взаимосвязи между социально-экономическими явлениями можно описать следующими типами моделей:

1.Линейная: y = a 0 +a1 x1 +...+a n x n .

2.Степенная: y = a 0 x1a1 x a22 ...x ann .

3.Показательная: y = ea0 +a1x1 +...+a n xn .

4.Параболическая: y = a 0 + a1x12 +... + a n x 2n .

Примером множественной нелинейной степенной регрессии является производственная функция Кобба-Дугласа:

Y = AKa Lb ,

показывающая зависимость реального объема выпуска Y от капитальных затрат K и затрат труда L . Для нахождения коэффициентов функции КоббаДугласа a и b прологарифмируем обе части равенства:

ln Y = ln(AKa Lb ),

ln Y = ln A + a ln K + b ln L .

Заменим:

ln Y = y ,

ln K = k , ln L =l , ln A = c .

Получим множественную линейную регрессию y = c + ak + bl . Коэффициенты a,b,c этой регрессии можно найти, решив систему трех линейных уравнений с тремя неизвестными, как было написано выше.

Экономическая интерпретация коэффициентов а и b функции Кобба-

Дугласа Y = AKa Lb : при увеличении капиталовложений на 1% от своего среднего значения реальный объем выпуска увеличится на a% от своего среднего значения, а при увеличении затрат труда на 1% от своего среднего значения реальный объем выпуска увеличится на b% от своего среднего значения.

2.2.Решение типовых задач

Задача 1. По группе стран мира имеются данные о средней ожидаемой продолжительности жизни населения, величине ВВП на начало 2003 года, суточной калорийности питания на душу населения, а также о коэффициенте младенческой смертности и численности населения. Данные представлены в приложении 1. Требуется:

1.На основании матрицы парных коэффициентов корреляции выделить два наиболее существенных фактора, от которых зависит средняя ожидаемая продолжительность жизни.

2.Написать уравнение множественной регрессии и вычислить его параметры.

3.Проинтерпретировать полученные коэффициенты уравнения.

4.Оценить значимость полученного уравнения и его коэффициентов.

5.Сделать выводы о возможности прогнозирования по данной модели.

Решение:

1. Матрица парных коэффициентов корреляции имеет вид:

Коэффициент корреляции R x1y ≈ 0.1154. Это говорит о том, что связь между средней ожидаемой продолжительностью жизни и величиной ВВП отсутствует (0,1154<0.3), а значит, величина ВВП не влияет на среднюю продолжительность жизни.

Коэффициент корреляции Rx 2 y ≈ 0.3109 . Это значит, что связь между средней ожидаемой продолжительностью жизни и суточной калорийностью питания прямая, но очень слабая (0,3<0.3109<0.5), следовательно, суточная калорийность питания влияет на среднюю ожидаемую продолжительность жизни очень незначительно, но в целом при увеличении (уменьшении) суточной калорийности питания средняя продолжительность жизни увеличивается (уменьшается).

Коэффициент корреляции показывает, что между средней продолжительностью жизни и коэффициентом младенческой смертности существует сильная обратная связь (0.7< |-0.74| ). Это говорит о том, что, в целом, при увеличении (уменьшении) коэффициента младенческой смертности средняя ожидаемая продолжительность жизни уменьшается (увеличивается).

Коэффициент корреляции Rx 4 y ≈ −0.2055 не значителен. А значит, связи между средней продолжительностью жизни и численностью населения нет (|-0.2055| < 0.3). Следовательно, изменение численности населения не отражается на средней продолжительности жизни.

На основании матрицы корреляции видно что, факторами, влияющими на среднюю продолжительность жизни, являются суточная калорийность питания и коэффициент младенческой смертности, а значит, для построения модели нужно использовать именно эти признаки. Но для правильного построения модели нужно проверить ее на мультиколлинеарность.

мультиколлинеарность в модели отсутствует.

Уравнение регрессии с учетом выбранных признаков имеет вид:

y = a 0 +a1x 2 +a 2 x3

Для нахождения коэффициентов a0, a1 и a2 необходимо решить следующую систему:

Решив систему получаем результат: a0=68.102, a1=0.0033,

a2=-0.262.

Коэффициент a0 не поддаётся интерпретации, поскольку сам по себе в данной модели он не имеет смысла (так как он показывает, что при нулевой суточной калорийности питания и нулевым коэффициентом младенческой смертности средняя ожидаемая продолжительность жизни была бы равна 68,102 года, а это невозможно).

Коэффициент а1 показывает что при увеличении (уменьшении) суточной калорийности питания на 1 кал. средняя ожидаемая продолжительность жизни в участвующих в исследовании странах увеличивается (уменьшается)

на 0,0033 года.

Коэффициент а2 показывает что при уменьшении (увеличении) коэффициента младенческой смертности на 1 единицу средняя продолжительность жизни в странах участвующих в исследовании увеличится (уменьшится) на 0,262 года.

Для оценки значимости уравнения регрессии необходимо оценить F- критерий Фишера:

Fрас=20,31,

Fтабл.=3,35,

Fрас> Fтабл, следовательно уравнение регрессии статистически значимо.

Для оценки статистической значимости коэффициентов a1 и a2 воспользуемся t – критерием Стьюдента:

ta1рас =1,89 ,

ta2рас = 5,84,

tтабл=2.05.

Проверка на значимость коэффициентов а1, а2 показала коэффициент а2 статистически значим (5,84>2.05), а коэффициент а1 статистически не значим(1,89<2.05). Такой результат, возможно, получился от того, что связь между суточной калорийностью питания и средней ожидаемой продолжительностью жизни слабая. В целом же уравнение статистически значимо.

Пример 2. Построить производственную функцию Кобба-Дугласа для оценки национального дохода США по следующим данным: Y – национальный доход США, млрд. долл., K – капиталовложения, млрд. долл., L – общее число занятых в экономике, тыс. чел.

Источник данных: www.bls.gov, www.economagic.com.

Произведем все необходимые вычисления в Excel, используя Сервис/ Анализ данных/Регрессия. В диалоговом окне ввода данных и параметров вывода входной интервал Y – колонка «lnY», а входной интервал X –

колонки «lnK» и «lnL».

Результаты множественной линейной регрессии ln Y = ln A + a ln K + b ln L представлены ниже:

Возвращаясь к исходным коэффициентам функции Кобба-Дугласа

Y = AKa Lb , получим:

lnA=0,862, A= 2,367.

Таким образом, производственная функция имеет вид: Y = 2,367 K0,956L0,129 . Это означает, что увеличении капиталовложений на 1% от своего среднего значения национальный доход США увеличивается на 0,956% от своего среднего значения, а при увеличении численности занятых в экономике на 1% от своего среднего значения национальный доход увеличится на 0,129 от своего среднего значения.

2.3. Задачи для самостоятельного решения

Задача 1. По статистической выборке данных с сайта www.vladhome.ru введите фиктивные переменные в исследование, опишите их. Вычислите матрицу парных корреляций, проанализируйте ее. На основании матрицы парных коэффициентов корреляции выделите два наиболее существенных фактора, от которых зависит цена квартиры. Напишите уравнение множественной регрессии. Вычислите его параметры. Проинтерпретируйте коэффициенты регрессии. Вычислите коэффициент множественной корреляции. Оцените с помощью коэффициента множественной детерминации качество построенной модели. Оцените значимость полученного уравнения регрессии. Оцените значимость коэффициентов регрессии. Сделайте вывод о возможности прогнозирования по данной модели. Проделайте расчеты в ППП MS Excel.

Задача 2. В результате исследования факторов, определяющих экономический рост, по 73 странам получено следующее уравнение регрессии:

где ~y - темпы экономического роста (темпы роста среднедушевого ВВП в % к базисному периоду); P – реальный среднедушевой ВВП, %; S – бюджетный дефицит, % к ВВП; I – объем инвестиций, % к ВВП; D – внешний долг, % к ВВП; In – уровень инфляции, %. Проверьте гипотезу о достоверности полученной модели в целом. До получения результатов этого исследования ваш однокурсник заключил с вами пари, что эмпирические результаты по данной модели покажут наличие обратной связи между темпами экономического роста и объемом внешнего долга страны (% к ВВП). Выиграл ли это пари ваш однокурсник?

Задача 3. По 20 предприятиям легкой промышленности получена следующая информация, характеризующая зависимость объема выпуска продукции y (млн. руб.) от количества отработанных за год человеко-часов x1 (тыс.чел.час.) и среднегодовой стоимости производственного оборудования x2 (млн. руб.):

Определите коэффициент детерминации в этой модели. Составьте таблицу результатов дисперсионного анализа. Проанализируйте полученные результаты регрессивного анализа.

Задача 4. По 50 семьям изучалось потребление мяса – y (кг на душу населения) от дохода – x1 (руб. на одного члена семьи) и от потребления рыбы – x2 (кг на душу населения). Результаты оказались следующими:

Используя t-критерий Стьюдента, оцените значимость параметров уравнения. Рассчитайте F-критерий Фишера. Оцените по частным F-критериям Фишера целесообразность включения в модель а) фактора x1 после фактора x2; б) фактора x2 после фактора x1.

Задача 5. Имеются следующие данные о ценах и дивидендах по обыкновенным акциям, а также данные о доходности компании. Построить линейное уравнение множественной регрессии и пояснить экономический смысл его параметров

Задача 6. Бюджетное обследование пяти случайно выбранных семей дало следующие результаты (в ден. ед.)

Оцените регрессию накоплений на доход и имущество. Спрогнозируйте накопления семьи, имеющей доход 40 ден. ед. и имущество стоимостью 25 ден. ед. Предположим, что доход семьи возрос на 10 ден. ед., в то время как стоимость имущества не изменилась. Оцените, как изменятся ее накопления. Оцените, как возрастут накопления семьи, если ее доход вырос на 5 ден. ед., а стоимость имущества увеличилась на 15 ден. ед.