
теория
.pdf
ДАЛЬНЕВОСТОЧНЫЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ТИХООКЕАНСКИЙ ИНСТИТУТ ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ И ТЕХНОЛОГИЙ
А. А. Кравченко
ЭКОНОМЕТРИКА
Владивосток
2005
Предисловие
В современных программах подготовки экономистов курс эконометрики занял одно из ключевых мест, поскольку сегодня деятельность в любой области экономики требует от специалиста применения современных методов оценки, анализа и интерпретации экономических данных.
Сегодня эконометрические методы применяются в качестве стандартных в различных отраслях прикладной экономики, изучающей все, начиная от расходов домашних хозяйств и предпринимательских инвестиций и заканчивая организацией производств, рынков труда и эффектами государственной политики.
Наиболее важная задача эконометрики состоит в том, чтобы количественно измерить связи между различными экономическими процессами и явлениями на основе имеющихся данных при помощи статистических методов, а также соответствующим образом интерпретировать и использовать полученные результаты. Следовательно, эконометрика – это взаимодействие экономической теории, наблюдаемых данных и статистических методов. Именно взаимодействие этих трех составляющих делает эконометрику интересной, многообещающей и, не самой легкой в понимании.
Свидетельством всемирного признания эконометрики является присуждение шести нобелевских премий по экономике за разработки в этой области: премия 1969 г. была присуждена Р. Фишеру и Я. Тинбергену за разработку математический методов анализа экономических данных; премия 1980 г. – Л.Клейну за построение макроэконометрических моделей, основанных на системах эконометрических уравнений; премия 1981 г. – Д. Тобину за регрессию с цензурированной зависимой переменной, которую по его имени называют тобит; премия 1989 г. – Т. Хаавелмо за анализ и оценивание систем одновременных уравнений; премия 2000 г. – Дж. Хекману и Д. Макфаддену за разработку теорию и методов, широко использующихся
встатистическом анализе поведения индивидуумов и семейных хозяйств; премия 2003 г. – Р. Энглу и К. Грэнжеру за работы в области коинтеграции временных рядов.
Учебное пособие составлено на основе курса лекций, читаемых автором
вИнституте менеджмента и бизнеса Дальневосточного государственного университета. Каждая глава учебного пособия состоит из теоретических основ, решения типовых задач и задач для самостоятельного решения. Некоторые задачи требуют творческого, исследовательского подхода.
Учебное пособие предназначено студентам, впервые приступающим к изучению эконометрики.

Глава 1. Парная регрессия и корреляция
1.1.Теоретические основы
Парной регрессией называется уравнение связи двух переменных y и х: y = f (x) ,
где y – зависимая переменная (результативный признак), x – независимая, объясняющая переменная (факторный признак). По форме связи регрессии делятся на линейные и нелинейные, а по числу входящих переменных – на парные и множественные.
В случае парной линейной регрессии рассматривается простейшая
модель
~ = + y ax b ,
где a, b - коэффициенты (параметры) регрессии. Для оценки этих коэффициентов пользуются самым популярным в эконометрике методом наименьших квадратов (МНК), суть которого состоит в минимизации суммы квадратов остатков:
n |
n |
~ |
2 |
n |
2 |
|
2 |
|
= ∑(yi − axi − b) |
→ min |
|||
S = ∑ei |
= ∑(yi − yi ) |
|
|
|||
i=1 |
i=1 |
|
|
i=1 |
|
, |
где y - фактическое |
значение результативного |
|
~ |
|||
|
признака; y - значение |
|||||
результативного признака, полученное путем подстановки в уравнение регрессии факторного признака.
Искомые коэффициенты являются решением системы нормальных уравнений:
∂S |
= −2( |
|
|
y |
|
− |
∑ |
ax |
|
− |
∑ |
b)= 0, |
|
||||||
|
∂a |
∑ |
|
|
i |
|
|
|
i |
|
|
|
|
||||||
|
∂S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−∑bx i |
)= 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||||||
|
|
= −2(∑yi x i − ∑axi |
|
||||||||||||||||
деля каждое уравнение на∂b |
(− 2n) и переходя к средним, получим систему двух |
||||||||||||||||||
линейных уравнений с двумя неизвестными: |
|
|
|
||||||||||||||||
|
|
|
|
|
− a |
|
− b = 0, |
|
|
|
|
||||||||
|
|
|
y |
x |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
yx − ax |
− bx |
= 0. |
|
|||||||||||||
|
|
|
|
|
|||||||||||||||
Выразим из системы двух уравнений с двумя неизвестными параметры a и b. Из первого уравнения
b = y − ax .
Подставив выражение для b во второе уравнение системы и выразив a, получим следующую формулу:
a = |
|
|
|
− |
|
|
|
|
|
|
|
||
xy |
y |
x |
|
||||||||||
|
|
|
|
− |
|
|
2 . |
|
|||||
|
|
|
x 2 |
|
|
||||||||
|
|
|
x |
|
|||||||||
~ |
= ax + b , где x и y – |
||||||||||||
Пусть получено следующее уравнение регрессии y |
|||||||||||||
переменные с простыми естественными единицами измерения. Тогда: увеличение x на 1 единицу (в единицах измерения x) приведет к увеличению значения y на a единиц (в единицах измерения y).

Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции для линейной регрессии:
r = |
xy |
− x y |
|
|
σxσy . |
||||
|
||||
Свойства коэффициента корреляции:
1.Абсолютная величина коэффициента корреляции не превосходит единицы: r ≤1.
2.Условие r = ±1 является необходимым и достаточным, чтобы y и x были связаны линейной функциональной зависимостью. Если регрессия является точно линейной и r = 0 , то между y и х нет линейной корреляционной зависимости.
3.Если коэффициент корреляции положительный, то связь между признаками прямая, т.е. с увеличением (уменьшением) x признак y увеличивается (уменьшается). Если коэффициент корреляции отрицательный, то связь между признаками обратная, т.е. с увеличением (уменьшением) x признак y уменьшается (увеличивается).
4.Если |r| от 0 до 0,3, то связь между признаками практически отсутствует; если от 0,3 до 0,5, то – слабая; если от 0,5 до 0,7, то – умеренная; если от 0,7 до 1, то сильная.
Одним из недостатков линейного регрессионного анализа является то,
|
|
~ |
= ax + b . |
что он может быть применен только к линейным уравнениям вида y |
|||
Например, уравнения вида y = a + |
b |
и y = ax b является нелинейным. Все |
|
x |
|||
нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.
Регрессии, нелинейные по объясняющим переменным: 9 полиномы разных степеней y = a +b1 x +b2 x 2 +b3 x 3 ,
y = a + b
9 равносторонняя гипербола x .
Регрессии, нелинейные по оцениваемым параметрам:
9степенная y = ax b ,
9показательная y = abx ,
9экспоненциальная y = ea+bx .

y y
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
|||
|
|
|
|
|
|
|
|
|
|
|
|
y= x |
|
|
|
|
|
|
|
|
|
a b |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
y= + /x |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
x |
0 |
|
|
x |
||||||||
|
|
|
|
|
|
|
|
y = a + |
b |
|
|
|
||||
Рассмотрим подробнее зависимости |
|
и y = ax b . |
Графически эти |
|||||||||||||
x |
||||||||||||||||
зависимости имеют вид, показанный на рисунке: |
|
|
|
|||||||||||||
|
y = a + |
b |
|
|
|
|
|
|
|
|
|
|
|
|||
1. |
x |
- это обратная зависимость между x и y. Это регрессия на |
||||||||||||||
|
|
|
||||||||||||||
основе гиперболы. Выведем оценки коэффициентов. Составляем функцию суммы квадратов остатков.
2 |
2 |
|
|
2 |
|
n |
2 |
n |
~ 2 |
n |
|
|
b 2 |
||||||
S = e1 |
+e2 |
+... +en |
= ∑ei |
= ∑(y − y ) = |
∑ y −a − |
|
|
= |
|||||||||||
|
|||||||||||||||||||
|
|
|
|
|
|
|
i =1 |
|
i =1 |
|
|
i =1 |
|
x |
|
||||
|
n |
|
2 |
|
2 |
|
b2 |
|
|
b |
|
b |
|
|
|
|
|
||
|
|
|
|
+ a |
|
+ |
|
|
− |
2ya − 2y |
|
+ 2a |
|
|
|
→ min |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||
|
= ∑ y |
|
|
x |
x |
x |
|
|
|
|
|||||||||
|
i =1 |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
||||
Для определения параметров a и b необходимо решить систему нормальных уравнений:
|
∂S |
= 0, |
|
|
|
|
|
|
|
|
|
|
|
∂a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂S |
= 0. |
|
|
|
|
|
|
|
|
|
|
|
∂b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂S |
|
|
|
|
n |
|
n |
1 |
|
|
|
|
|
= 2an − 2∑y + 2b∑ |
|
=0, |
|
|||||||
∂a |
x |
|
||||||||||
|
|
|
|
i =1 |
|
i=1 |
|
|
|
|||
|
∂S |
n |
1 |
|
n |
y |
|
|
n |
1 |
|
|
|
|
|
|
|
||||||||
|
|
= 2b∑ |
|
|
|
− 2∑ |
|
+ 2a∑ |
|
=0. |
||
∂b |
x |
2 |
|
x |
x |
|||||||
|
i=1 |
|
|
i =1 |
|
|
i =1 |
|
||||
Деля уравнение на 2n, получим:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||
a − y +b |
|
|
|
= 0, |
|
|
|
|
||||||||||
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
y |
|
|
1 |
|
|
||||||||||
b |
|
|
|
− |
|
|
|
+ a |
|
|
= 0. |
|||||||
|
2 |
|
|
|
||||||||||||||
|
x |
|
|
x |
|
|
x |
|
|
|||||||||
Решая систему двух уравнений с двумя неизвестными, получим

a= y −b 1 ,
x
|
1 |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
1 |
|
||||||||||
b |
|
|
|
|
− |
|
|
+ y −b |
|
|
= 0, |
||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
|
x2 |
|
|
|
x |
|
|
x |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
y |
− y |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
b = |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
|
1 |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||||
|
|
|
x |
|
x |
|
|
|
|
|
|||||||||||||||||
2. Рассмотрим |
теперь функцию y = ax b (это степенные функции). |
||||||||||||||||||||||||||
Обнаружим, |
что соотношение y = ax b может быть преобразовано в линейное |
||||||||||||||||||||||||||
уравнение путем использования логарифмов. Прологарифмируем обе части этого тождества:
ln y = ln ax b = ln y + b ln x .
Заменим ln y = y′, ln x = x′, ln a = a′, тогда y′= a′+ bx′, т.е. получим линейную функцию. В этом случае процедура оценивания параметров состоит в следующем:
1. Вычислить y′ и x′ для каждого наблюдения путем взятия логарифмов от исходных данных.
2. Оценить линейную зависимость y′= a′+ bx′, в результате чего получим оценки a′ и b. Здесь b является непосредственной оценкой, а a′ является оценкой ln a .
3. Переход к прежним переменным: a′ ln a , ea′ a - оценка a. Тесноту связи между признаками для нелинейных регрессий оценивает
индекс корреляции для нелинейной регрессии (0 ≤ ρ ≤1):
∑( − ~)2
y y
ρ = 1 − ∑(y − y)2 .
При анализе можно также рассчитывать среднюю ошибку аппроксимации – среднее отклонение расчетных значений от фактических:
|
|
|
|
|
|
~ |
|
|
|
||
|
|
|
|
|
|
|
|
||||
|
|
= |
1 |
∑ |
|
|
y − y |
|
|
100% |
|
A |
|||||||||||
|
|
~ |
|||||||||
|
|
|
n |
|
|
|
y |
|
|
. |
|
|
|
|
|
|
|
|
|||||
Допустимый предел значений A – не более 8-10%.
Проверить значимость уравнения регрессии значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных для описания зависимой переменной.
F-тест – оценивание качества уравнения регрессии – состоит в проверке
гипотезы H0 о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического
и критического (табличного) значений F-критерия Фишера. определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:
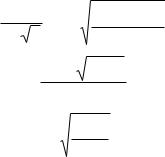
|
|
~ |
2 |
/ m |
|
2 |
|
||
F |
= |
∑(y |
− y) |
|
= |
rxy |
(n −2) |
||
~ |
|
−m −1) |
|
||||||
факт |
|
2 |
2 |
, |
|||||
|
|
∑(y − y ) /(n |
1−rxy |
||||||
где n – число единиц совокупности, m – число параметров при переменных x.
Fтабл - это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости α . Уровень значимости α - вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно α принимается равной 0.05 или 0.01.
Если Fтабл < Fфакт , то гипотеза H0 - гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая
значимость и надежность. Если же Fтабл > Fфакт , то гипотеза H0 не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стьюдента и доверительные
интервалы для каждого показателей. Выдвигается гипотеза H0 о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью t-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки:
tb = |
b |
|
t а = |
а |
|
t r = |
r |
|
|
mb , |
mа , |
mr . |
|||||||
|
|
|
|||||||
Случайные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам:
|
S |
ост |
|
|
|
|
|
~ |
2 |
|
ma = |
|
S = |
∑(y − y) |
|
|
|||||
σx |
n |
, |
|
n |
− 2 |
, |
|
|||
|
|
|
|
|
||||||
|
mb = |
Sост |
∑x 2 |
|
|
|
||||
|
|
|
σx n |
|
, |
|
|
|||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1−r2 |
|
|
|
|
|
|
|
mrxy |
= |
|
|
xy |
|
|
|
|
|
|
|
n −2 . |
|
|
|
||||
|
|
|
|
|
|
|
|
|||
Сравнивая фактическое и критическое (табличное) значения t- |
||||||||||
статистики - tтабл (при n-2 степенях свободы) |
и |
tфакт - принимаем или |
||||||||
отвергаем гипотезу H0 . |
|
|
|
|
|
|
|
|
|
|
Если tтабл < tфакт , то H0 отклоняется, т.е. a, b, |
rxy |
не случайно отличаются |
||||||||
от нуля и сформировались под влиянием систематически действующего фактора x. Если tтабл > tфакт , то гипотеза H0 не отклоняется и признается
случайная природа формирования a, b, rxy .
Для расчета доверительного интервала определяем предельную ошибку ∆ для каждого показателя:
∆a = tтабл ma , ∆b = tтабл mb .

Формулы для расчета доверительных интервалов имеют следующий
вид:
|
γa = a ± ∆a , γaьшт |
= a −∆a , γaьфч |
= a ± ∆a , |
|
||||||||
|
γ |
b |
= b ± ∆ |
b , |
γb |
= b −∆b |
, |
γb |
= b ± ∆b |
. |
|
|
|
|
|
|
ьшт |
|
ьфч |
|
|
||||
Прогнозное значение |
yp определяется путем подстановки в уравнение |
|||||||||||
~ |
+ b соответствующего (прогнозного) значения xp . |
|
||||||||||
регрессии y = ax |
|
|||||||||||
Экстраполяция кривой регрессии, т.е. ее использование вне пределов |
||||||||||||
обследованного |
диапазона |
значений объясняющей переменной |
может |
|||||||||
привести к значительным погрешностям, поэтому при определении прогнозного значения строят и доверительные интервалы прогноза.
Вычисляется средняя ошибка прогноза m :
|
|
|
1 |
|
(x p − x)2 |
|
|
|
|
|
|
|
|
|
m = s 1 + |
|
+ |
∑(x − x)2 |
|
|
|
|
|
|
|
∑(y − y ) |
n |
, |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
s = |
~ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
γ |
~ |
|
± ∆~ |
|
где |
|
n − m −1 ; и строится доверительный интервал прогноза |
= y |
p |
|||||||
|
|
|
y p , |
||||||||
где ∆н~з |
= tтабл m . |
|
|
|
|
|
|
|
|
|
|
Величина стандартной ошибки достигает минимума при и возрастает по мере удаления от среднего значения в обе стороны. Результаты прогноза ухудшаются в зависимости от того, насколько прогнозное значение отклоняется от области наблюдений значений фактора x.
На графике доверительные границы для прогноза представляют собой гиперболы, расположенные по обе стороны от линии регрессии.
Экстраполяция кривой регрессии, т.е. ее использование вне пределов обследованного диапазона значений объясняющей переменной может привести к значительным погрешностям, поэтому при определении прогнозного значения строят и доверительные интервалы прогноза:
|
|
|
|
* |
|
|
|
2 |
|
|
1 |
|
(x* − x)2 |
|
|
|
* |
|
|
2 |
|
|
1 |
|
(x* − x)2 |
|
|
|
|
|
y |
|
− t1−α,т−2 |
|
s |
|
1 |
+ |
|
+ |
|
2 |
|
; y |
|
+ t1−α,т−2 |
s |
|
1 |
+ |
|
+ |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
∑(x − x) |
|
|
|
|
|
|
|
|
n ∑(x − x) |
|
||||
|
|
2 |
|
∑(y − y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
||||||
|
s |
|
= |
|
~ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
|
|
n − 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
В |
|
силу воздействия |
неучтенных |
случайных |
факторов и |
причин |
||||||||||||||||||||
отдельные наблюдения y будут в большей или меньшей степени отклоняться от функции регрессии f(x). В этом случае в общем виде уравнение взаимосвязи двух переменных может быть представлено в виде:
y = f (x) + u ,
где u – случайная переменная, характеризующая отклонение от функции регрессии. В случае парной линейной зависимости модель имеет вид:
y = ax + b + u .
Гомоскедастичность – условие «одинакового разброса», т.е. вероятность того, что величина u примет какое-то положительное (отрицательное)

данное значение, будет одинаковой для всех наблюдений, т.е. σ 2 (ui ) = const ,
i . Гетероскедастичность – условие «неодинакового разброса», σ2 (ui ) =σi2 - дисперсия не обязательно одинакова для всех наблюдений i.
Если СКО остатков растет по мере увеличения x. Поле корреляции такой
y
0 |
|
x |
гетероскедастичной модели представлено ниже:
Вариация y при больших значениях х гораздо больше, чем при малых значениях х. Зависимость y от x может вполне пригодиться для практических приложений, но результаты, связанные с анализом точности модели, оценкой значимости и построением доверительных интервалов, могут оказаться непригодными. Например, при небольших выборках есть риск получить оценку параметров, существенно отличающуюся от истинного параметра.
Очень часто проявление проблемы гетероскедастичности можно предвидеть заранее, основываясь на знании характера статистических данных. В таких случаях можно предпринять соответствующие действия по устранению этого эффекта еще на этапе спецификации модели, т.е. на этапе формулировки вида модели.
Рассмотрим два теста, в которых делаются различные предположения о зависимости между средним квадратическим отклонением случайного члена и величиной объясняющей переменной.
1. Тест ранговой корреляции Спирмена. При выполнении теста Спирмена предполагается, что среднее квадратическое отклонение случайной переменной либо увеличивается, либо уменьшается по мере увеличения x.
Этапы проведения теста:
1.Ранжируются значения x. Ранг – порядковый номер значения x. Ранжирование – упорядочивание. Если значения совпадают, то им присваивается ранг, равный среднему арифметическому из суммы мест, которые они занимают.
2.Вычисляются отклонения фактических значений от расчетных (остатки). Ранжируются остатки.

3. |
Вычисляется |
коэффициент |
ранговой |
корреляции |
по |
формуле |
||
|
r |
=1− |
6∑Di2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x,e |
|
n(n2 −1) , где Di - разность между рангом x и рангом остатков. |
|||||
|
|
|
||||||
4. |
Вычисляется |
t-статистика |
rx,e n −1 . |
Определяется |
по |
таблицам |
||
|
критерия Стьюдента при уровне значимости α табличное значение |
|||||||
|
при бесконечном числе степеней свободы. |
|
|
|||||
5.По этому критерию гипотеза об отсутствии гетероскедастичности будет отклонена при уровне значимости α, если тестовая статистика
rx,e  n −1 превышает табличное значение.
n −1 превышает табличное значение.
2. Тест Голдфелда-Квандта. При проведении проверки по этому критерию, предполагается, что стандартное отклонение σi распределения
вероятностей случайного члена ui пропорционально значению xi в этом наблюдении. Предполагается, что случайный член распределен нормально и не подвержен автокорреляции.
Все n наблюдений упорядочиваются по x. Оцениваются отдельные
регрессии для |
первых |
n′ |
и последних |
n′наблюдений, |
а |
средние |
||||
n − 2n′наблюдений |
отбрасываются. Если |
предположение |
о |
природе |
||||||
гетероскедастичности верно, |
то дисперсия случайного члена в последних n′ |
|||||||||
наблюдениях будут больше, |
чем в первых n′. Обозначая сумму квадратов |
|||||||||
|
|
|
|
|
|
|
RSS1 |
|
|
|
остатков через |
RSS |
и |
RSS |
2 , рассмотрим их отношение |
RSS2 |
. |
Эта величина |
|||
1 |
|
|
||||||||
имеет F-распределение с n′− k −1 и n′− k −1 степенями свободы, где k |
– число |
|||||||||
объясняющих переменных в регрессионном уравнении.
Для оценки коэффициентов регрессии с гетероскедастичностью применяется взвешенный метод наименьших квадратов, этапы которого следующие:
1.Оценивают обычным методом наименьших квадратов регрессию y на x. Вычисляют столбец квадратов остатков.
2. |
Оценивают |
коэффициенты |
регрессии квадратов |
остатков на |
x2 : |
|||||
|
e2 = a0 + a1 x2 . |
Вычисляют набор значений, каждое из которых равно |
||||||||
|
корню из соответствующего расчетного значения |
~ |
2 |
. Этот вектор |
||||||
|
e |
|
||||||||
|
называется набор весов, на эти значения делятся исходные значения |
|||||||||
|
y и x . |
|
|
|
|
|
|
|
|
|
|
|
X = |
x |
Y = |
y |
|
|
|
|
|
3. |
Вычисляют |
|
~2 |
, |
~2 |
. Оценивают регрессию Y на |
X. |
|||
|
e |
e |
||||||||
Оценивают регрессию методом наименьших квадратов.
1.2.Решение типовых задач
Пример 1. По данным приложения 6 о прожиточном
минимуме (x), среднемесячной заработной плате (y) построить
