дискретка / Лекция 7

Лекция 7.

п.7. Графы. Орграфы.

7.5. Представление графов в компьютере.

Известны различные способы представления графов в памяти компьютера, которые различаются объемом занимаемой памяти и скорости выполнения операций над графами. Преставление выбирается, исходя из потребностей конкретной задачи. В подавляющем большинстве случаев граф задается матрицей. Чаще всего графы представляют либо матрицей смежности, либо матрицей инциденций.

Определение 7.12. Матрица смежности вершин орграфа G, содержащего n вершин- это квадратная матрица A=a_ij n-го порядка, у которой строки и столбцы матрицы соответствуют вершинам орграфа. Элементы a_ij матрицы A равны числу дуг, направленных из i-й вершины в j-ю. Если орграф состоит из однократных дуг, то элементы матрицы равны либо 0, либо 1.

Матрицей смежности вершин неориентированного графа G, содержащего n вершин, называют квадратную матрицу A=a_ij n-го порядка, у которой строки и столбцы матрицы соответствуют вершинам неориентированного графа. Элементы a_ij матрицы A равны числу ребер, направленных из i-й вершины в j-ю. В случае неориентированного графа G ему вместе с ребром (v_i, v_j) принадлежит и ребро (v_j, v_i), поэтому матрица смежности вершин A=a_ij будет симметрична относительно главной диагонали.

Определение 7.13. Матрица смежности дуг орграфа - это квадратная матрица B=b_ij m-го порядка, у которой строки и столбцы матрицы соответствуют дугам орграфа. Элементы b_ij матрицы B равны 1, если дуга e_i непосредственно предшествует дуге e_j и 0 в остальных случаях.

Матрицей смежности ребер неориентированного графа является матрица B=b_ij m-го порядка, у которой строки и столбцы матрицы соответствуют ребрам графа. Элементы b_ij матрицы B равны 1, если ребра e_i и e_j имеют общую вершину, и 0 в остальных случаях.

Определение 7.14. Матрицей инциденций (инцидентности) неориентирован-ного помеченного графа с вершинами и ребрами называется матрица размерности , строки которой соответствуют вершинам, а столбцы – ребрам. Элементы матрицы инциденций неориентированного графа равны 1, если вершина инцидентна ребру , и 0 в противном случае.

Матрицей инциденций (инцидентности) орграфа с вершинами и дугами называется матрица размерности nm, строки которой соответствуют вершинам, а столбцы -дугам орграфа. Элементы c_ij равны 1, если дуга e_j исходит из i-й вершины; -1, если дуга e_j заходит в i-ю вершину; 0, если дуга не инцидентна i-й вершине:

Если каждому ребру графа приписано некоторое положительное число, то такое число называется весом, а сам граф называется взвешенным графом. Простой взвешенный граф (сеть) может быть представлен также своей матрицей весов , где _ij – вес ребра, соединяющего вершины v_i и v_j. Весы несуществующих ребер (дуг) полагают равными нулю или бесконечности в зависимости от приложений.

Пример 7.7. 1) Для заданного неориентированного графа построить матрицы смежностей и матрицы инциденций.

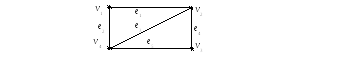
2) Для заданного ориентированного графа построить матрицы смежностей и матрицы инциденций.

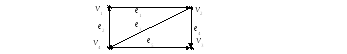
Решение. 1) Строим матрицу смежности вершин, которая будет размерности 44. Строим матрицу смежности ребер, которая будет размерности 55.

, .

Строим матрицу инциденций, которая будет размерности 45.

.

2) Строим матрицу смежности вершин, которая будет размерности 44. Строим матрицу смежности ребер, которая будет размерности 55.

,

Строим матрицу инциденций, которая будет размерности 45.

.



7.6. Выявление маршрутов с заданным количеством ребер (дуг).

С помощью матрицы смежности вершин можно найти все маршруты, содержащие заданное количество ребер (дуг). Справедлива следующая теорема, которую примем без доказательства.

Теорема 7.3. Для определения маршрутов, состоящих из k ребер (дуг), необходимо возвести в k-ю степень матрицу смежности вершин P. Тогда элемент матрицы даст количество маршрутов длины k (состоящих из k ребер) из вершины в вершину .

Пример 7.8. Для неориентированного графа, изображенного на рисунке, найти все маршруты длины 2.

Решение. Составим матрицу смежности вершин P и возведем ее в квадрат. Результат возведения:

.

Рассмотрим первую строку. Например, элемент . Это значит, что существует три маршрута из v₁ в v₁ длиной в два ребра. Действительно, это маршруты . Из v₁ в v₂ существует два маршрута: .

Если использовать числовую матрицу смежности вершин, то для нахождения самих маршрутов необходимо работать с графом. Если воспользоваться модифициро-ванной матрицей смежности, в ячейки которой записаны названия ребер, то можно получить не только количество маршрутов, но и сами маршруты.

Действительно, для данного примера имеем



Аналогично обстоит дело с орграфом, хотя у него матрица смежности вершин несимметрическая.

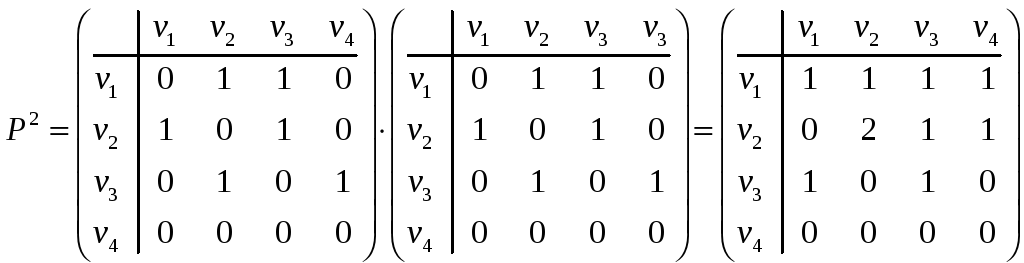
Пример 7.9. Для орграфа, изображенного на рисунке, найти все маршруты с тремя дугами.

Решение. Матрица смежности P и результаты ее возведения в квадрат и куб имеют следующий вид:

,

.

Рассмотрим, например, элемент после возведения матрицы смежности вершин в квадрат. Это значит, из вершины v₂ в вершину v₂ есть два маршрута длиной две дуги. Это маршруты и . После возведения матрицы в куб сохраняется та же картина. Например, . Это значит, что есть два маршрута длиной три дуги из вершины v₁ в вершину v₂. Это маршруты и . 

Для получения цепей (маршрутов, в которых каждое ребро встречается один раз) нужно в модифицированной матрице P ³ вычеркнуть те слагаемые, в которых какой-либо сомножитель встречается более одного раза.

7.7. Упорядочивание вершин и дуг орграфа.

Расчеты в задачах, связанных с графами, заметно упрощаются, если их элементы упорядочены. Под упорядочиванием вершин связного орграфа без циклов понимают такое разбиение его вершин на группы, при котором:

1) вершины первой группы не имеют предшествующих вершин, а вершины последней группы последующих;

2) вершины любой другой группы не имеют предшествующих в следующей группе;

3) вершины одной и той же группы дугами не соединяются.

Аналогичным образом вводится понятие упорядочения дуг. В результате упорядочения элементов получают орграф, изоморфный исходному. Упорядочение элементов выполняется графическим или матричным способом. Графический способ упорядочивание вершин, дуг орграфа носит название алгоритма Фалкерсона.

Алгоритм Фалкерсона для упорядочения вершин:

1. Находят вершины графа, в которые не входит ни одна дуга. Они образуют первую группу. Нумеруют вершины группы в натуральном порядке 1, 2, ... . При этом присвоение номеров вершинам внутри группы может быть сделано не единственным образом, что не имеет значения.

2. Мысленно вычеркиваем все пронумерованные вершины и дуги, из них выходящие. В получившемся графе найдется, по крайней мере, одна вершина, в которую не входит ни одна дуга. Этой вершине, входящей во вторую группу, присваивается очередной номер и т.д. Этот шаг повторяется до тех пор, пока все вершины не будут упорядочены (пронумерованы).

Алгоритм Фалкерсона для упорядочения дуг:

1. Найти дуги, не имеющие непосредственно предшествующих (они образуют I группу).

2. Вычеркнуть найденные дуги; после этого появится, по крайней мере, одна новая дуга, не имеющая непосредственно предшествующей (в графе без дуг I группы). Такие дуги составляют II группу. Повторять этот шаг, пока все дуги не будут разбиты на группы. В заключение упорядочения дугам присваивают новые обозначения с индексами 1, 2, ... .

__________________________________

Пример 7.11. Графическим способом упорядочить вершины и дуги заданного орграфа.

Решение. Используя алгоритм Фалкерсона, упорядочим вершины и дуги заданного орграфа.

_________________________________