Практикум по электричеству и электротехнике / LAB10

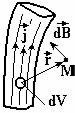
Б.Н. Сипливый, В.К. Михайлов,

В.В. Подгорный, П.И. Поленичкин.

Практикум по электричеству

Лабораторная работа №10

Исследование механического

взаимодействия контуров с токами

Целью работы является экспериментальная проверка закона Био-Савара путем исследования механического взаимодействия контуров с токами, а также измерение тока на основе этого взаимодействия (абсолютный метод).

5.2.1. Теоретические сведения

Если точечный заряд q движется равномерно со скоростью v относительно выбранной системы координат, то в точке наблюдения М возникает магнитное поле В:

где r — радиус-вектор, проведенный от заряда к точке наблюдения; k — размерный коэффициент, зависящий от выбора системы единиц. В системе СИ:

C другой стороны, если в некоторой области пространства на точечный заряд q, движущийся в выбранной системе координат со скоростью v, действует сила:

то говорят, что в этой области существует магнитное поле B. Сила, определяемая выражением

(3) называется магнитной составляющей силы Лоренца. Таким образом, магнитное поле определяется выражениями (1), (3). Существенно, что это определение имеет смысл только по отношению к конкретной системе, так как в другой системе, движущейся относительно выбранной, магнитное поле будет уже другим и, в частности, может вообще отсутствовать.

Из определения (1) легко получить выражение для магнитного поля провода с током, как результат векторного сложения магнитных полей дрейфующих в проводе электрических зарядов. Пусть dV — элементарный объем металлического проводника, в котором протекает электрический ток плотности j:

где n — концентрация свободных электронов; e — заряд электрона; vd — скорость дрейфа электронов. Проведем радиус-вектор r от объема dV к точке наблюдения М магнитного поля В, как показано на рис.5.2.1. Объем dV можно считать точкой по сравнению с r, поэтому для каждого электрона проводимости внутри dV справедливо выражение (1). Применяя принцип суперпозиции ко всем

зарядам внутри dV, с учетом (4) получим выражение для магнитного поля dB элемента тока объемом dV:

Выражение (5) называется законом Био-Савара для массивного проводника. Магнитное поле всего проводника находится с помощью принципа суперпозиции интегрированием (5) по объему проводника с током плотности j.

Аналогичным образом, из определения (3) легко получить выражение для силы, действующей со стороны магнитного поля В на элемент провода с током, как сумму сил, дейст-

2

вующих на отдельные движущиеся в проводе заряды. Пусть dV — элементарный объем проводника с током плотности j, который находится в магнитном поле B (поле В может быть как собственным, так и полем внешних источников) Тогда сила dF, действующая на элемент dV провода согласно (3) и (4), будет:

Выражение (6) называется законом Ампера для массивного проводника. Полная сила в соответствии с принципом суперпозиции находится интегрированием по объему про-

где: dl — элемент линейного провода, направленный вдоль вектора плотности тока j; I — полный ток в проводе; r — вектор, проведенный от dl к точке наблюдения магнитного поля dB

(рис.5.2.2).

Закон Ампера для линейного проводника примет вид:

Заметим, что закон Био-Савара, записанный в виде (7) недоступен для опытной проверки, так как реально стационарный ток может протекать лишь в замкнутом контуре. Применим принцип суперпозиции к замкнутому контуру с током I. Тогда выражение (7) примет вид:

Формулы (8) и (9) совместно определяют характер взаимодействия двух проводников с токами. Рассмотрим представляющий в данной работе интерес частный случай взаимодействия двух прямых параллельных отрезков тонкого провода одинаковой длины l на расстоянии h друг от друга, по которым текут одинаковые токи I (рис.5.2.3). Пусть некоторый элемент dl1 первого провода имеет координату x1, а элемент dl2 второго — x2. Элемент dl1 согласно (7) создает в точке (x2,h) магнитное поле:

где r12={x2 x1,h}. В этом поле, согласно (8) на элемент dl2 действует сила:

Из анализа двойного векторного произведения (10) можно заключить, что если элементы dl1 и dl2 параллельны, т.е. токи текут в одну сторону, то сила dF21 антипараллельна оси z, а аналогичная сила dF12, действующая на элемент dl1 в магнитном поле В2 верхнего провода и равная по величине dF21 направлена по оси z (см. рис.5.2.3). Таким образом, параллельные отрезки провода с одинаково направленными токами притягиваются. Если же dl1 dl2, то силы dF12 и dF21 меняют направления на противоположные, что соответствует отталкиванию отрезков провода с антипараллельными токами.

Чтобы определить величину силы взаимодействия между отрезками l1 и l2, сначала раскроем двойное векторное произведение

(10):

dl1 r12 eydl1r12 sin ey dl1h;

3

dl2 dl1 r12 ex ey dl2dl1h ez hdl1dl2 ,

где ex, ey, ez — орты декартовых координат. Введем обозначения: dl1=dx1, dl2=dx2. Тогда (10) можно переписать в виде:

Опуская далее знаки векторов, вычислим модуль полной силы, действующей на отрезки l1 и l2:

Интеграл от f(x1) теперь легко берется , так что окончательно для модуля силы F21 c учетом (2) получится:

Из формулы (12) видно, что при l два тонких параллельных провода, по которым текут одинаковые токи I, притягиваются (или отталкиваются) в вакууме с силой

на каждый метр длины (здесь h — расстояние между проводами). Ток, который при h=1 м вызывает взаимодействие тонких параллельных бесконечно длинных проводов в вакууме с силой F*=2 10 7 Н/м, называется Ампером, (это определение единицы тока в системе СИ).

В работе измеряется сила отталкивания двух квадратных рамок, расположенных параллельно друг против друга, по которым текут одинаковые и противоположно направленные токи (рис.5.2.4). Пусть I — ток, обтекающий каждую из рамок, h — расстояние между ними, l — длина стороны рамки. Будем интересоваться силами, имеющими ненулевые проекции на ось z (силы, направленные вдоль x и y, компенсируются силами реакции подвеса рамок и в работе не измеряются).

Рассмотрим взаимодействие одной из сторон нижней рамки с параллельными по отношению к ней сторонами верхней. Сторона 1 отталкивается от 1 с силой F1 1, определяемой из (12). Сторона 3 притягивается к 1, т. к. токи в них текут в одну сторону. Для вычисления модуля в формулу (12) вместо h следует подставить (h2+l2)1/2, тогда:

Но нас интересует нормальная к обеим рамкам компонента F3 1 (z-компонента), поэтому:

4

Подсчитаем z-компоненту силы взаимодействия F2 1 перпендикулярно скрещенных сторон 2 и 1. Раскрывая (10) и учитывая, что dl1 dl2 , для двойного векторного произведения получаем:

0тсюда видно, что сила F2 1, действующая на сторону 2 направлена вдоль dl1 и не имеет z- компоненты. То же самое справедливо по отношению к стороне 4 . Таким образом, верхняя рамка в целом отталкивается вверх от стороны 1 нижней рамки с силой F1 =F1 1 F3 1(z), а так как все стороны нижней рамки эквиваленты, то общая сила отталкивания двух рамок будет:

Формула (13) неудобна для экспериментальной проверки, поэтому целесообразно ограничиться приближением:

Так как в формуле (13) отношение l/h везде входит в квадрате, то можно считать, что условие (14) выполняется даже при h 0,2l.

Задачей экспериментальной части работы является проверка соотношения (15), вытекающего из определения магнитного поля (1-3), а также законов (7), (8) и определяющего зависимости F(I) и F(h).

5.2.2. Экспериментальная установка

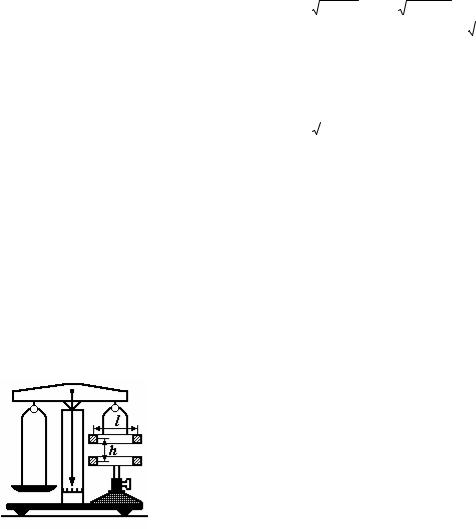
Экспериментальная установка представляет собой коромысловые весы, к одному плечу которых подвешена чашка для гирь, а к другому - одна из квадратных рамок с несколькими десятками витков провода (рис.5.2.5). Точно такая же рамка закреплена на стойке. Ослабив стопорный винт, стойку вместе с нижней рамкой можно перемещать по вертикали, изменяя тем самым расстояние h между рамками. Параллельность рамок устанавливается юстировочными винтами в основании стойки. Измерение именно отталкивания рамок и как следствие — выбор именно такого их взаимного расположения, как показано на рис.5.2.5, связаны с тем, что притягивающиеся рамки не удалось бы устойчиво уравновесить.

Линейные размеры поперечного сечения обмоток рамок можно считать малыми по сравнению с длиной стороны l и расстоянием h. Такое приближение хотя и приводит к определенной ошибке, особенно при небольших h, но без него расчет силы взаимодействия рамок неоправданно бы усложнился. Размеры l и h берутся между центрами сечений обмоток, как показано на рис. 5.2.5.

Рамки соединяются друг с другом последовательно, но так, чтобы токи в них протекали в противоположных направлениях, что легко устанавливается по характеру взаимодействия рамок. Рамки питаются от источника постоянного тока; величина тока определяется амперметром. Число витков в рамках N и длина стороны l указаны на установке; расстояние h фиксируется по прикрепленной линейке.

Устройства, подобные описанному выше, находят применение в так называемых токовых весах, служащих для измерения тока абсолютным методом в метрологических лабораториях.

6

5.2.5.Контрольные вопросы и задания

1.Определение магнитного поля.

2.Определение единицы тока в системе СИ.

3.Вывести закон Био-Савара из определения магнитного поля.

4.Вычислить на основе формулы (10) характер и силу взаимодействия двух параллельных и перпендикулярно скрещенных отрезков проводов с токами.

5.Вычислить магнитное поле в центре квадратной рамки.

6.Какие силы будут действовать на рамку с током, помещенную в однородное магнитное поле, параллельное плоскости рамки?

7.Почему два параллельных электронных пучка в вакууме отталкиваются, а два провода с одинаково направленными токами притягиваются?

5.2.6.Литература

1.С.Г. Калашников. Электричество. М.: Наука, 1985. §§ 75, 76,78-80,83,85.

2.Р. Фейнман и др. Фейнмановские лекции по физике. Т.5. Электричество и магнетизм. М.:

Мир, 1977. гл. 13: §§ 1,3,4,6.

3.Э. Парселл. Электричество и магнетизм. (Берклеевский курс физики, т.3) М.: Наука, 1983. § 6.1.