Downloads / Статы (1) / Статы / помощь предков / Минимум

9

Экзаменационная программа курса

«Статистическая радиофизика»

1. Минимальные требования

1. Дать определение частоты появления события и сформулировать аксиому измерений.

Если серии из N экспериментов с определённым комплексом условий событие А, соответствующее определённому результату, появилось n раз, то отношение  = n/N называется частотой появления события A при N экс­пе­ри­ментах. Для количественной характеристики статистической закономерности вво­дит­ся число р, мало отличающееся от  при больших N и называемое веро­ят­ностью случайного события А. Утверждение, что для каждого случайного события А существует определённая вероятность p = P{A}, означает, что в любых достаточно длинных сериях экспериментов частоты  появления события А будут приблизительно одинаковы и близки к р.

Предположение, что , называется аксиомой измерения. Естественно, 0  P{A}  1.

2. Записать формулу полной вероятности и формулу Байеса.

можно ввести условную вероятность P{A|B} события A при условии, что произошло событие B

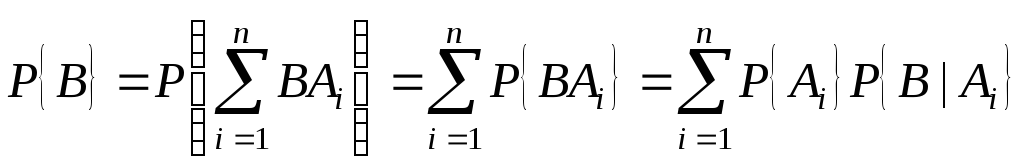формула полной вероятности. получаем формулу Байеса:

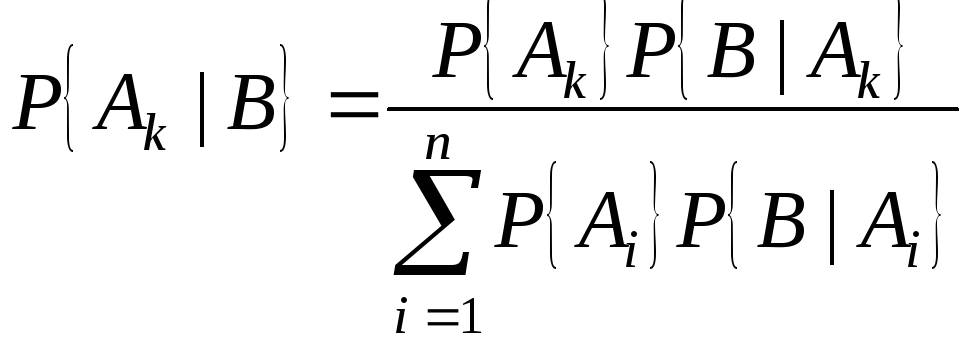. (Ошибка! Текст указанного стиля в документе отсутствует..0)

3. Сформулировать закон больших чисел и теорему Бернулли.

Значит, теорема Чебышева, или закон больших чисел

теорема Бернулли.

_N – среднее арифметическое из N случайных попарно независимых величин, имеющих равномерно ограниченную дисперсию, то есть D(_i)  С

4. Записать формулы для распределений Гаусса, Релея и Пуассона.

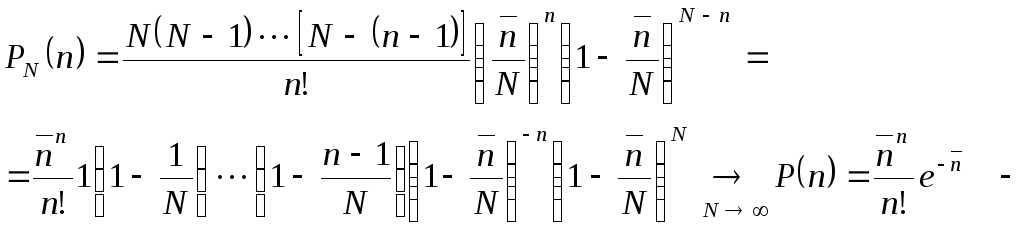распределение Пуассона.

–распределение Муавра – Лапласа

– нормальное распределение, или распределение Гаусса

5. Дать определение характеристической функции и записать выражения, связывающие ее с функцией плотности вероятности

Характеристической функцией случайной величины  называется среднее значение случайной величины exp(iu): .

6. Сформулировать центральную предельную теорему.

Пусть ₁, …, _N – независимые случайные величины, <_i> = a_i,

M₂(_i) = _i² < C < . Если для любого  > 0

,

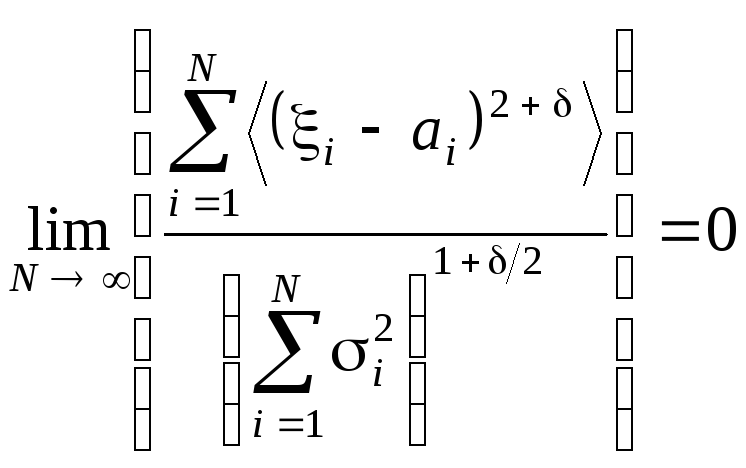то случайная величина имеет распределение, равномерно стремящееся к нормальному при N  , независимо от распределения слагаемых

7. Записать выражение для плотности вероятности одномерной функции случайной величины.

8. Привести вид пуассоновского импульсного процесса, сформулировать предположения, при которых он рассматривается и записать выражение для вероятности появления n импульсов на интервале [0, t].

9. Сформулировать условия, при которых распределение пуассоновского импульсного процесса близко к нормальному.

10. Сформулировать теорему Кемпбелла для пуассоновского импульсного процесса.

11. Дать определения непрерывности, дифференцируемости, интегрируемости и стационарности случайной функции.

Случайная функция (t) называется непрерывной в среднеквадратичном, если , то есть ; непрерывной по вероятности, если , и непрерывной почти наверняка, если . так же определяется и дифференцируемость случайной функции, как существование в каком-либо смысле предела . В тех же трех смыслах можно понимать существование интеграла, как предела суммы вида 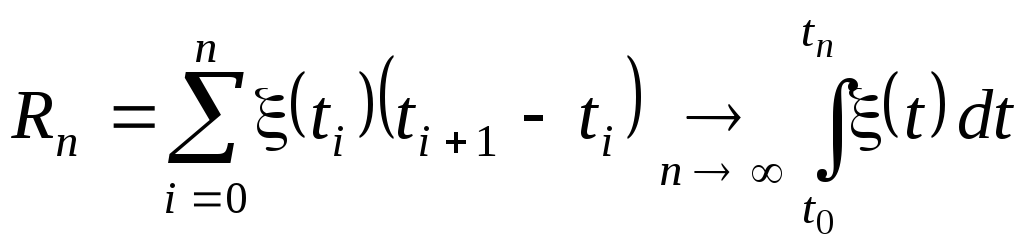. Случайная функция (t) называется стационарной, или однородной по t, если для всех ее конечномерных распределений при любом  выполняется условие

_n(t₁ + , x₁, …, t_n + , x_n) = _n(t₁, x₁, …, t_n, x_n)

12. Дать определение коэффициента корреляции случайной функции.

Часто упо­т­реб­ля­ется также нормированный коэффициент корреляции

.

D[(t)] дисперсия случайного процесса. Центральный смешанный момент второго порядка (t₁, t₂)

13. Дать определение среднего по времени и записать условие Слуцкого для эргодичности случайного процесса.

находить среднее по времени за интервал Т вида:

Условие называется условием эргодичности Слуцкого для стационарных процессов

14. Доказать, что функция автокорреляции стационарного случайного процесса ограничена по модулю.

Кроме того, автокорреляционная функция ограничена по модулю. Положим B(t₂, t₁) = |B|exp(i) и рассмотрим при произвольном a величину

Так как это равенство выполняется при произвольном a, и |cos( – a)|  1, то

.

15. Сформулировать соотношение неопределенностей и привести минимизирующие его функции.

()²()²  1/2 – соотношение неопределенностей.

Заметим, что равенство в формуле имеет место лишь для гауссовых кривых:.To есть гауссовы кривые вида (4.9) являются минимизирующими.

G(i) называется спек­т­ра­льной плотностью интенсивности случайного процесса. Функция автокорреляции В()

16. Дать определение белого шума и привести его функцию автокорреляции и спектральную плотность интенсивности.

Случайный процесс, для которого спектральная плотность интенсивности постоянна, называется белым шумом.

B() = 2G₀() дельта-коррелированный процесс.

17. Записать спектральную плотность интенсивности процесса на выходе линейной системы, на вход которой воздействует случайный процесс.

где – частотная характеристика системы

18. Сформулировать теорему о нормализации.

Пусть теперь процесс на входе ₁(t) не гауссов, но система узкополосная, то есть  << ₁, где  – интервал частот, на котором отлична от нуля АЧХ системы k(); ₁ – интервал частот, на котором отлична от нуля спектральная интенсивность G₁(i) случайного процесса на входе. С учётом соотношения неопределённостей (4.8) это условие с учетом формулы (4.17) принимает вид: _k << _p, где _k – интервал корреляции процесса ₁(t); _p – интервал релаксации, определяемый условием h( > _p) = 0. Выберем интервал , удовлетворяющий ус­ловию _k <<  << _p, и перепишем интеграл Дюамеля (5.1) в виде:

,

где .

Поскольку  >> _k, можно считать, что величины _n некоррелированы, по­э­то­му процесс ₂(t) представляет собой сумму большого числа не­кор­ре­ли­ро­ван­ных случайных величин и в силу центральной предельной теоремы является га­ус­сов­ым (нормальным) процессом. Это утверждение называется теоремой о нор­мализации.

19. Записать выражение для спектра колебаний с флуктуирующей частотой и привести формулы для случаев, когда наблюдаются медленные и большие или малые и быстрые флуктуации частоты.

?????

где (t) = d(t)/dt – девиация мгновенной частоты

20. Записать выражения для смещенной и несмещенной оценок автокорреляционной последовательности.

Оценка G_Т(i) называется несмещенной, если и состоятельной, если .

21. Записать выражения для периодограмм Даньелла и Уэлча.

22. Дать определение марковского процесса и получить уравнение Смолуховского.

Тот факт, что для задания марковской случайной функции достаточно двух детерминированных функций, позволил значительно развить теорию марковских случайных процессов и получить ряд фундаментальных результатов, например связи между вероятностями перехода для трех каких-либо последовательных моментов времени t₁ < t₂ < t₃. Для момента t₃ условие согласования (3.2) и определение (7.2) марковского процесса позволяют записать соотноше­ние:

.

Если известно, что (t₁) = x₁, то это соотношение принимает вид:

.

Но по определению марковского процесса v(t₃, x₃|t₁, x₁, t₂, x₂) = v(t₃, x₃|t₂, x₂), сле­довательно:

. (Ошибка! Текст указанного стиля в документе отсутствует..0)

Соотношение (7.6) называется уравнением Смолуховского.

23. Записать уравнение ФПК, пояснить смысл его коэффициентов и привести условия, при котором оно существует.

уравнение Фоккера – Планка – Колмогорова

,

Начальные условия его v(t₀, x|t₀, x₀) = (x – x₀). При этом функция v(t, x|t₀, x₀) должна быть неотрицательна и нормирована к единице

24. Записать распределение стационарного случайного процесса с независимыми прираще­ниями и выражение для его дисперсии.

является стационарной случайной функцией с независимыми приращениями. (t) – случайная дельта-коррелированная сила с нулевым средним значением

25. Записать дифференциальное уравнение для среднего функции F(x).

– дифференциальное уравнение для средних значений функции F(x).

26. Записать теорему Найквиста и сформулировать условия ее применимости.

G_e() = kTR()/ = kTRe[Z()]/ – теорема Найквиста.

27. Записать выражение для спектральной плотности интенсивности дробового шума.

28. Записать соотношения для спектральной плотности интенсивности шумов полупроводникового диода, биполярного и полевого транзисторов.

29. Привести выражение для дисперсии напряжения на выходе усилителя. Дать определение отношения сигнал/шум.

Поскольку случайный процесс u_2n(t) и детерминированный отклик не коррелированы, для среднего квадрата (дисперсии) выходного напряжения u₂(t), полагая u_2n(t) = u_2s(t) = 0, получаем:

n = [u_s(t)]²/[u_n(t)]² – отношение сигнал/шум

30. Записать связь функции автокорреляции и спектральной плотности интенсивности однородного стационарного случайного поля.