
MATLAB_Lab_pdf_only / Лабораторная работа 5 matlab
.pdf
Лабораторная работа №5
Использование MatLab\SciLab при решении задач вычислительной математики
Системы MatLab\SciLab обладают большими возможностями программирования и визуализации результатов научных исследований при решении задач вычислительной математики. Численные методы в этих системах предлагаются уже в виде готового инструментария — набора функций, их реализующих. Задачей данной работы является ознакомление с наиболее часто встречающимися на практике численными методами, которые используются при решении обыкновенных дифференциальных уравнений.
Исследование поведения систем и устройств в динамике, а также решение задач теории колебаний обычно базируется связано с решением обыкновенных дифференциальных уравнений (ОДУ) или их систем с начальными или граничными условиями. Одним из самых распространѐнных случаев является задача о решении системы дифференциальных уравнений первого порядка (кроме того, многие задачи можно свести к ней)
с граничными условиями , где – начальные и конечные точки интервала, на котором нужно найти решение. Решением такой задачи является векторная функция , удовлетворяющая как уравнению (1), так и граничным условиям. Независимая переменная х необязательно означает одну из пространственных координат, в общем случае решение дифференциальных уравнений может зависеть от произвольных переменных (обобщенных координат) или как зависимость от времени. На практике часто встречается система дифференциальных уравнений в форме Коши, которая записывается аналогично (1), но граничные условия задаются только на одной из границ – начальные условия, т.е. вектор вида .
Для решения дифференциальных уравнений второго и более высоких порядков их необходимо представить в виде системы дифференциальных уравнений первого порядка. Возможны дифференциальные уравнения, не разрешенные относительно производной:
. (2)
Такие уравнения либо трудно, либо невозможно, либо нежелательно приводить аналитическими методами к форме (1). Тем не менее, при их решении численными методами можно сначала разрешить уравнение (2) численно относительно производной для определения при заданных х и y, а далее воспользоваться одним из методов решения ОДУ.
Кроме ОДУ MatLab также может оперировать и с дифференциальными алгебраическими уравнениями (ДАУ, или differential-algebraic equations – DAEs). Методы решения ОДУ и ДАУ являются основой математического моделирования динамических линейных и нелинейных систем. Автоматическое их составление и решение реализованы в пакетерасширении Simulink.
Для решения систем ОДУ в MatLab реализованы различные численные методы в виде функций, называемых решателями – solvers. С их помощью можно найти решение в виде таблицы значений функции-решения в заданных точках на заданном интервале между граничными значениями. В частности, имеются следующие функции:
•ode45 – одношаговые явные методы Рунге-Кутта 4-го и 5-го порядков
вмодификации Дорманда и Принца. Это классический метод, рекомендуемый для начальной пробы решения. Во многих случаях он дает хорошие результаты, если система решаемых уравнений нежесткая.
•ode23 – одношаговые явные методы Рунге-Кутта 2-го и 4го порядков
вмодификации Богацки и Шампина. При умеренной жесткости системы ОДУ и низких требованиях к точности этот метод может дать выигрыш в скорости решения.
•ode113 – многошаговый метод Адамса–Башворта–Мултона переменного порядка класса предиктор–корректор. Это адаптивный метод, который может обеспечить высокую точность решения.
•ode15s – многошаговый адаптивный метод переменного порядка (от 1 до 5, по умолчанию 5), использующий формулы численного «дифференцирования назад». Его стоит применять, если решатель ode45 не обеспечивает решения и система дифференциальных уравнений жесткая.
•ode23s – одношаговый метод, использующий модифицированную формулу Розенброкка 2-го порядка. Может обеспечить высокую скорость вычислений при низкой точности решения жесткой системы дифференциальных уравнений.
•ode23t – неявный метод трапеций с интерполяцией. Этот метод дает хорошие результаты при решении задач, описывающих колебательные системы с почти гармоническим выходным сигналом. При умеренно жестких системах дифференциальных уравнений может дать высокую точность решения.
•ode23tb – неявный метод Рунге–Кутта в начале решения и метод, использующий формулы «дифференцирования назад» 2-го порядка в последующем.
•bvp4c – служит для проблемы граничных значений систем дифференциальных уравнений вида (1). Решаемые им задачи называют двухточечными краевыми задачами, поскольку решение ищется при задании граничных условий как в начале, так и в конце интервала решения.
Все перечисленные солверы могут решать системы уравнений явного вида , причем для решения жестких систем уравнений рекомендуется использовать только специальные решатели ode15s, ode23s, ode23t, ode23tb.
Синтаксис вызова функций для решения систем дифференциальных уравнений (под именем solver подразумевается любая из представленных выше функций) имеет следующий вид:
[X, Y] = solver(@F, tspan, y0) интегрирует систему дифференциальных уравнений вида на интервале tspan с начальными условиями y0. @F – дескриптор ODE-функции (можно также задавать функцию в виде 'F'). Каждая строка в массиве решений Y соответствует значению времени, возвращаемому в векторе-столбце T.
[X,Y] = solver(@F, tspan, y0, options) дает решение, подобное описанному выше, но с параметрами, определяемыми значениями аргумента options. options – аргумент, создаваемый функцией odeset. Она позволяет вывести или изменить параметры, установленные по умолчанию или с помощью функции odeset. Обычно используемые параметры включают допустимое значение относительной погрешности RelTol (по умолчанию 1e– 3) и вектор допустимых значений абсолютной погрешности AbsTol (все компоненты по умолчанию равны 1e–6).
Пример.
Решить задачу Коши dy/dx = 2(x2 + y2), y(0) = 1, 0<x<1.
Выполним решение данной задачи с помощью программы ode45. Вначале в М-файл записываем правую часть уравнения, сам М-файл оформляется как файл - функция, даем ему имя RHP:
function dydx = RHP(x, у)
dydx = zeros(l,l);
dydx = 2*(х^2+у^2);
return
Для численного решения задачи Коши в окне команд набираются следующие операторы:
>>[Х Y] = ode45(@F, [0 1], [1]);
>>plot (X,Y);
Уравнение решено, график построен!
В SciLab решение систем ОДУ производится с помощью функции
[y, w, iw] = ode([type],y0,x0,x [,rtol [,atol]],f [,jac] [,w,iw])
в которой y0 – вектор начальных условий, y – вектор для возврата решения, x0 – начальная точка интервала интегрирования, x – вектор координат узлов сетки, в которых производится поиск решения, f – функция правой части системы – это обязательные параметры. Т.е. для решения уравнения (1) с начальным условием y(x0) = y0, надо использовать команду:
y=ode(y0, x0, x, f).
Необязательные параметры этой функции:
type – задает метод решения или тип решаемой задачи. Возможные значения: stiff – решение жесткой задачи; adams – метод предикторкорректор Адамса; rk – метод Рунге-Кутта 4-го порядка; rkf – пятиэтапный метод Рунге-Кутта 4-го порядка; fix - метод Рунге-Кутта 4-го порядка с фиксированным шагом. Примечание: эти параметры являются строками, их необходимо взять в кавычки, например, 'fix'.
rtol, atol – относительная и абсолютная погрешности вычислений, вектор, размерность которого совпадает с размерностью вектора y; по умолчанию rtol=0.00001, atol=0.0000001, при использовании параметров rkf и fix - rtol=0.001, atol=0.0001.
jac – матрица, представляющая собой якобиан правой части жесткой системы ОДУ, задают матрицу в виде внешней функции вида J = jak(t, y).
w, iw – векторы для хранения информации о параметрах интегрирования, которые применяют для того, чтобы последующие вычисления выполнялись с теми же параметрами.
Рассмотрим использование функции на примере следующих задач.
Пример 1.
Решить задачу Коши dy/dx + y = sin(xy), y(x = 0) = 1.5.
Перепишем уравнение следующим образом: dy/dx = - y + sin(xy). Далее представим его в виде внешней функции и применим функцию:
y = ode(y0, x0, x, f),
в качестве параметров которой будем использовать:
f - ссылка на предварительно созданную функцию f(x, y) правой части; t - координаты сетки; x0, y0 - начальное условие y(x = 0) = 1.5; y - результат работы функции, т.е. решение задачи.
Код:
-->function yd = f(x, y), yd = -y+sin(y*x); endfunction;
-->y0 = 1.5; x0 =0; x = 0:1:35;
-->y = ode(y0, x0, x, f);
-->plot(x, y)
Пример 2.
Решить задачу Коши
на интервале [0; 10].
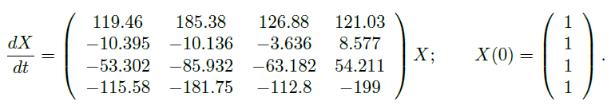
Сначала определяем файл-функцию правой части: //Функция, описывающая правую часть системы ОДУ function dy=syst(t,y)
dy = zeros(2,1);
dy(1) = cos(y(1)*y(2)); dy(2) = sin(y(1) + y(2)*t); endfunction
Далее в командной строке (или в файле) находим решение системы аналогично примеру 1:
--> x0=[0;0];
--> t0 = 0; t = 0:0.1:10; --> y = ode(x0, t0, t, syst); --> plot(t,y)
Пример 3.
Решить жесткую задачу Коши для системы из четырех ОДУ :
Решение системы в командной строке будет выглядеть следующим образом: -->B=[119.46 185.38 126.88 121.03;-10.395 -10.136 -3.636 8.577;
-->-53.302 -85.932 -63.182 -54.211;-115.58 -181.75 -112.8 -199]; -->function dx=syst1(t,x), dx=B*x,endfunction
-->function J=Jac(t,y),J=B,endfunction -->x0=[1;1;1;1]; t0=0; t=0:0.01:5; -->y=ode("stiff",x0,t0,t,syst1,Jac); plot(t,y); xgrid();

Задания.
1.Найти решение ОДУ вида x'' + x = 0 на отрезке [0, 2π] с начальным условием x(0) = 0 и x’(0) = 1 методом Рунге-Кутта 4–го порядка. Вывести таблицу значений и график. Сравнить с аналитическим решением.
2.Найти решение ОДУ со следующими правой частью и начальными условиями
