Вектор Шепли

Материал из Википедии — свободной энциклопедии

Перейти к: навигация,поиск

Вектор Шепли— принцип оптимальности распределения выигрыша между игроками в задачах теориикооперативных игр. Представляет собой распределение, в котором выигрыш каждого игрока равен его среднему вкладу в благосостояние тотальной коалиции при определенном механизме ее формирования.

Формальное определение

Для кооперативной игры рассмотрим некоторое упорядочение множества игроков N. Обозначим черезподмножество, содержащееiпервых игроков в данном упорядочении. Вкладомi-го по счету игрока назовем величину, гдеv— характеристическая функция кооперативной игры.

Вектором Шепли кооперативной игры называется такое распределение выигрыша, в котором каждый игрок получает математическое ожидание своего вклада в соответствующие коалиции , при равновероятном возникновении упорядочений:

где n— количество игроков,T— множество упорядочений множества игроковN,— распределение выигрыша, в котором игрок, стоящий на местеiв упорядочении, получает свой вклад в коалицию(точка Вебера).

Более распространенная формула для вычисления вектора Шепли, не требующая нахождения n! точек Вебера, имеет вид:

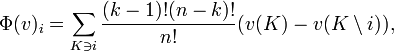
где n— количество игроков,k— количество участников коалицииK.

Аксиоматика вектора Шепли

Вектор Шепли удовлетворяет следующим свойствам:

1. Линейность.Отображениепредставляет собой линейный оператор, то есть для любых двух игр с характеристическими функциямиvиw

и для любой игры с характеристической функцией vи для любого

2. Симметричность.Получаемый игроком выигрыш не зависит от его номера. Это означает, что если играwполучена из игрыvперестановкой игроков, то ее вектор Шеплиесть векторс соответствующим образом переставленными элементами.

3. Аксиома болвана.Болваномв теории кооперативных игр называется бесполезный игрок, не вносящий вклада ни в какую коалицию, то есть игрокi, такой что для любой коалицииK, содержащейi, выполнено:.

Аксиома болвана состоит в том, что если игрок i— болван, то.

4. Эффективность.Вектор Шепли позволяет полностью распределить имеющееся в распоряжении тотальной коалиции благосостояние, то есть сумма компонент вектораравна.

Теорема Шепли.Для любой кооперативной игрыvсуществует единственное распределение выигрыша, удовлетворяющее аксиомам 1 — 4, задаваемое приведенной выше формулой.

Литература

1. Васин А. А., Морозов В. В. Теория игр и модели математической экономики - М.: МГУ, 2005, 272 с.

2. Воробьев Н. Н. Теория игр для экономистов-кибернетиков — М.: Наука, 1985

3. Мазалов В. В. Математическая теория игр и приложения — Изд-во Лань, 2010, 446 с.

4. Петросян Л. А., Зенкевич Н. А., Шевкопляс Е. В. Теория игр — СПб: БХВ-Петербург, 2012, 432 с.

5. Печерский С. Л., Яновская Е. Б. Кооперативные игры: решения и аксиомы — Изд-во Европейского ун-та в С.-Петербурге, 2004, 459 с.

Антагонистическая игра

Антагонистическая игра(игра с нулевой суммой,англ.zero-sum) — терминтеории игр. Антагонистической игрой называетсянекооперативная игра, в которой участвуют дваигрока, выигрыши которых противоположны.

Формально антагонистическая игра может быть представлена тройкой <X,Y,F>, гдеXиY— множествастратегийпервого и второго игроков, соответственно;F— функция выигрыша первого игрока, ставящая в соответствие каждой паре стратегий (ситуации) (x,y),действительное число, соответствующее полезности первого игрока при реализации данной ситуации. Так как интересы игроков противоположны, функцияFодновременно представляет и проигрыш второго игрока.

Исторически антагонистические игры являются первым классом математических моделей теории игр, при помощи которых описывались азартные игры. Считается, что благодаря этому предмету исследования теория игр и получила свое название. В настоящее время антагонистические игры рассматриваются как часть более широкого класса некооперативных игр.

Пример

X \ Y	Орел	Решка
Орел	-1, 1	1, -1
Решка	1, -1	-1, 1

Простейшим примером антагонистической игры является игра «Орлянка». Первый игрок прячет монету орлом или решкой вверх, а второй пытается угадать, как она спрятана. Если он не угадывает — он платит первому одну денежную единицу, если угадывает — первый платит ему одну денежную единицу.

В данной игре каждый участник имеет две стратегии: «орел» и «решка». Множество ситуаций в игре состоит из четырех элементов. В строках таблицы указаны стратегии первого игрока х, в столбцах — стратегии второго игрокаy. Для каждой из ситуаций указаны выигрыши первого и второго игроков.

В аналитическом виде функция выигрыша первого игрока имеет следующую форму:

где x∈Xиy∈Y— стратегии первого и второго игроков, соответственно.

Так как выигрыш первого игрока равен проигрышу второго, то .

Если результат полностью определяется игроком, совершившим последний ход (если правила хода идентичны для игроков), стратегия может быть найдена с помощью функции Гранди.