
- •Теория игр
- •. Содержание
- •История исследований по теории игр
- •Представление игр
- •Экстенсивная форма
- •Нормальная форма
- •Характеристическая функция в игре
- •Применение теории игр
- •Описание и моделирование
- •Нормативный анализ (выявление наилучшего поведения)
- •Типы игр Кооперативные и некооперативные
- •Симметричные и несимметричные
- •С нулевой суммой и с ненулевой суммой
- •Параллельные и последовательные
- •С полной или неполной информацией
- •Игры с бесконечным числом шагов
- •Дискретные и непрерывные игры
- •Метаигры
- •Стохастическая игра
- •История исследований стохастических игр
- •Применение стохастических игр
- •Некооперативная игра
- •Некооперативная игра в нормальной форме
- •Некооперативная игра в развернутой форме
- •Принципы оптимальности Эффективность по Парето
- •Равновесие Нэша: формальное определение
- •Равновесии дрожащей руки: формальное определение
- •Собственное равновесие
- •Определение
- •Сильное равновесие
- •Равновесие в доминирующих стратегиях
- •Равновесие, совершенное по под-играм
- •Кооперативная игра
- •Математическое представление кооперативной игры
- •Свойства характеристической функции
- •Примеры кооперативных игр
- •Решение кооперативных игр
- •Свойства
- •Формальное определение
- •История возникновения
- •Дальнейшие свойства
- •Вектор Шепли
- •Формальное определение
- •Аксиоматика вектора Шепли
- •Литература
- •Антагонистическая игра
- •Дифференциальные игры
- •Сетевые игры
- •Кооперативные стохастические игры
- •Марковский процесс принятия решений
- •Определение
- •Классическая дилемма заключённого
- •Обобщённая форма
- •Примеры из реальной жизни
- •Повторяющаяся дилемма заключённого
- •Психология обучения и теория игр
- •Восточная философия
- •Генетика
- •Игрок в теории игр
- •Типы стратегий
- •Терминология
- •Формальные определения
- •Доминирование и равновесие Нэша
- •Последовательное исключение доминируемых стратегий
- •Литература
Свойства
Эквивалентным является определение С-ядра кооперативной игры в терминах блокирования распределений выигрыша коалициями. Говорят, что коалиция Kблокирует распределение выигрышаx, если найдётся другое распределение выигрышаy, такое, что
![]() ,
,
и для любого участника
![]() выполнено
выполнено![]() .
.
Тогда С-ядром кооперативной игры называется множество распределений выигрыша, которые не могут быть заблокированы ни одной коалицией.
С-ядро задаётся системой линейных уравнений и нестрогих линейных неравенств, в связи с чем оно является выпуклыммногогранником.
С-ядро может быть пустым. Достаточные условия непустоты ядра были сформулированы Л.Шепли:
Теорема.Кооперативная игра ссупермодулярнойхарактеристической функцией имеет непустое ядро.
Необходимые и достаточные условия непустоты ядра были сформулированы О.Бондаревойи, позднее,Л.Шепли:
Теорема.Ядро кооперативной игры непусто тогда и только тогда, когда онасбалансирована.
Любое равновесие Вальрасапринадлежит ядру, однако обратное неверно. Однако, при некоторых предположенях, если количество агентов в экономике стремится к бесконечности, ядро стремится ко множеству равновесий Вальраса (гипотезаЭджворта).
N-ядро
N-ядро,пред-N-ядро(nucleolus,prenucleolus) —решениякооперативных игр, основанные на минимизации степени неудовлетворённости выигрышем подмножеств участников игры (коалиций).
|
|
Формальное определение
Обозначим через e(x)для каждого допустимого распределения выигрышей x в кооперативной игре (N,v) векторэксцессоввсех коалиций, с элементами, упорядоченными по возрастанию.
Рассмотрим некоторое множество распределений выигрышей A. N-ядромкооперативной игры относительно множества Aназывается точка x, соответствующая минимуму отношениялексикографического порядкана множестве всевозможных векторовe(x)для x принадлежащих A.
В случае когда множество A совпадает с множеством всех допустимых распределений выигрышей, соответствующее N-ядро называется пред-N-ядром игры (N,v). Если же A совпадает с множеством дележей, то соответствующее N-ядро называется N-ядром игры (N,v).
Интуитивно N-ядро представляет распределение выигрыша, на котором степень неудовлетворённости самых неудовлетворенных коалиций, измеряемая величиной их эксцесса, будет наименьшей.
История возникновения
Впервые N-ядро было введено Шмайдлером (Schmeidler) в 1969 году. Шмайдлер рассматривал именно N-ядро (то есть лексикографичекий минимум на множестве дележей, а не всех распределений выигрышей). Впоследствии большее распространение получило пред-N-ядро, ввиду большого количества интересных свойств, однако, так как термин «N-ядро» уже был занят, оно стало называться «пред-N-ядром».
Шмайдлер доказал существование и единственность N-ядра, также показал, что оно лежит в K-ядре и непрерывно зависит от значений характеристической функции игры v.
Дальнейшие свойства
Характеризация посредством сбалансированности
В 1971 году Колберг доказал элегантную характеризацию пред-N-ядра в терминах сбалансированных наборов коалиций.
Его теорема гласит, что данное распределение
выигрышей является N-ядром тогда и только
тогда, когда для любого вещественного
числа
![]() верно,
что набор коалиций с эксцессом больше
верно,
что набор коалиций с эксцессом больше![]() является
сбалансированным набором.
является
сбалансированным набором.
Связь с другими решениями
1. Пред-N-ядро всегда содержится в K-ядре. Обычно именно так показывают непустоту K-ядра для любой игры.
2. Если C-ядро непусто, то пред-N-ядро содержится в С-ядре.
Другие свойства
Пред-N-ядро обладает свойствами анонимности,ковариантности, удовлетворяетаксиоме болванаи являетсясогласованным решениемв смыслеДевиса-Машлера.
Вычислительная сложность
Пред-N-ядро отличается от других известных
решений неконструктивностью своего
определения. Нахождение N-ядра с помощью
его определения является весьма
трудоемким даже для игр с небольшим
числом игроков (так как речь идет о
поиске лексикографического минимума
на множестве векторов в пространстве
размерности
![]() ,
где n равно количеству игроков в игре).
,
где n равно количеству игроков в игре).
Из-за этого большое распространение в последние годы получили задачи, связанные с нахождением пред-N-ядра за ограниченное число действий (полиномиально зависящее от количества игроков в игре) для отдельных классов игр.
K-ядро
Материал из Википедии — свободной энциклопедии
Перейти к: навигация,поиск
K-ядро(от англ.kernel) — принцип оптимальности вкооперативных играх, впервые введен в работе М. Дэвиса и М. Машлера (1965).
Пусть задана кооперативная игра с
характеристической функцией
![]() и
и![]() —эффективныйвектор выигрышей.Максимальный излишекигрока
—эффективныйвектор выигрышей.Максимальный излишекигрока![]() над
игроком
над
игроком![]() по
отношению к
по
отношению к![]() определяется
как
определяется
как
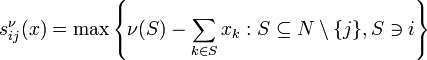 .
.
Максимальный излишек представляет
собой наибольший выигрыш, который игрок
![]() может
получить, войдя в какую-либо частичную
коалицию
может
получить, войдя в какую-либо частичную
коалицию![]() без
кооперации с игроком
без
кооперации с игроком![]() ,
в предположении, что остальные игроки
в составе коалиции
,
в предположении, что остальные игроки
в составе коалиции![]() удовлетворены
выигрышами, которые доставляет им
распределение
удовлетворены
выигрышами, которые доставляет им
распределение![]() .
Он представляет собой способ измерения
сравнительной переговорной силы игроков.K-ядромкооперативной игры
.
Он представляет собой способ измерения
сравнительной переговорной силы игроков.K-ядромкооперативной игры![]() называется
множестводележей
называется
множестводележей![]() ,
удовлетворяющих условиям:
,
удовлетворяющих условиям:
![]() ;
;
![]() ;
;
для всех пар игроков
![]() .
.
Интуитивно, игрок
![]() имеет
большую переговорную силу, чем игрок
имеет
большую переговорную силу, чем игрок![]() при
дележе
при
дележе![]() ,
если
,
если![]() ,
но игрок
,
но игрок![]() защищен
от угроз игрока
защищен
от угроз игрока![]() ,
если
,
если![]() ,
так как в этом случае он может получить
выигрыш
,
так как в этом случае он может получить
выигрыш![]() без
кооперации. K-ядро содержит все дележи,
при которых ни один игрок не имеет такой
переговорной силы ни над каким другим
игроком.
без
кооперации. K-ядро содержит все дележи,
при которых ни один игрок не имеет такой
переговорной силы ни над каким другим
игроком.
