 ЗАДАНИЕ N 9 сообщить об ошибке
ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Интервальные оценки параметров распределения
Дан доверительный интервал |
для оценки математического ожидания нормально |
распределенного количественного признака. Тогда при увеличении объема выборки этот доверительный интервал может принять вид :
 ЗАДАНИЕ N 10 сообщить об ошибке
ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Характеристики вариационного ряда
Мода вариационного ряда 1, 1, 2, 2, 2, 3, 3, 4, 5, 5, 5, , 7, 7, 7, 8, 8, 10, 11 равна 5. Тогда значение  равно :
равно :
5
6
19
7
 ЗАДАНИЕ N 11 сообщить об ошибке
ЗАДАНИЕ N 11 сообщить об ошибке
Тема: Сетевое планирование и управление
Матрица коэффициентов прямых затрат линейной статической модели Леонтьева имеет вид
, а объемы валовых выпусков представлены вектором |
. Тогда |
объемы конечного продукта будут представлены вектором :
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191832[05.04.2012 23:43:09]
Решение:
Статическая линейная модель Леонтьева в матричной форме моделируется системой , где - единичная матрица. Следовательно, объемы конечного продукта
определяются как |
, то есть |
ЗАДАНИЕ N 12 сообщить об ошибке |
|
Тема: Производственные функции |
|
Производственная функция |
характеризуется убывающей отдачей от масштаба. |
Тогда параметры  и
и  могут принимать значения :
могут принимать значения :
 ,
, 
 ,
, 
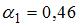 ,
, 
 ,
, 
 ЗАДАНИЕ N 13 сообщить об ошибке
ЗАДАНИЕ N 13 сообщить об ошибке
Тема: Функции спроса и предложения
Равновесный объем спроса-предложения равен , а равновесная цена спроса-предложения равна
 . Тогда функции спроса
. Тогда функции спроса  и предложения
и предложения  могут иметь вид :
могут иметь вид :
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191832[05.04.2012 23:43:09]
 ,
, 
 ,
, 
 ,
, 
 ,
, 
ЗАДАНИЕ N 14 сообщить об ошибке |
|
|
Тема: Функции полезности |
|
|
Функция полезности потребителя имеет вид |
, а бюджетное ограничение |
. |
Тогда оптимальный набор благ потребителя равен : |
|
|
, |
|
|
, |
|
|
, |
|
|
, |
|
|
 ЗАДАНИЕ N 15 сообщить об ошибке
ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Линейное программирование: графическое задание области допустимых решений
Область допустимых решений ABCDE задачи линейного программирования имеет вид:
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191832[05.04.2012 23:43:09]
Тогда минимальное значение функции  равно :
равно :
6
0
18
12
 ЗАДАНИЕ N 16 сообщить об ошибке
ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Транспортная задача
В транспортных задачах
A)
B)
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191832[05.04.2012 23:43:09]
оптимальное распределение поставок :

 имеет задача B
имеет задача B
 имеет задача A
имеет задача A
 имеет и задача A и задача B
имеет и задача A и задача B  не имеет ни одна из задач
не имеет ни одна из задач
Решение:
В оптимальном распределении сумма потенциалов для свободных клеток должна быть меньше или равна тарифу: . Для задачи A, например,  . То
. То
есть, решение неоптимальное. Для задачи B:
.
.
.
. То есть, решение оптимальное. Следовательно, оптимальное распределение имеет задача В.
 ЗАДАНИЕ N 17 сообщить об ошибке
ЗАДАНИЕ N 17 сообщить об ошибке
Тема: Сетевое планирование и управление
Для сетевого графика, изображенного на рисунке,
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191832[05.04.2012 23:43:09]
критический путь имеет вид  . Тогда значение параметра
. Тогда значение параметра  не может быть равно :
не может быть равно :
19
12
13
16
 ЗАДАНИЕ N 18 сообщить об ошибке
ЗАДАНИЕ N 18 сообщить об ошибке
Тема: Теория игр: игры с природой
Матрица выигрышей в игре с природой имеет вид:
Тогда соответствующая ей матрица рисков будет иметь вид :
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191832[05.04.2012 23:43:09]
 ЗАДАНИЕ N 19 сообщить об ошибке
ЗАДАНИЕ N 19 сообщить об ошибке
Тема: Свойства определенного интеграла
Определенный интеграл |
равен : |
0
1
 ЗАДАНИЕ N 20 сообщить об ошибке
ЗАДАНИЕ N 20 сообщить об ошибке
Тема: Асимптоты графика функции
Наклонная асимптота графика функции  задается уравнением вида :
задается уравнением вида :
Решение:
Прямая |
является наклонной асимптотой графика функции |
при |
( |
|
), если существуют конечные пределы: |
|
|
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191832[05.04.2012 23:43:09]
,  , или соответственно
, или соответственно
,  .
.
|
|
. |
Следовательно, прямая |
является наклонной асимптотой графика данной функции |
как при |
, так и при |
. |
 ЗАДАНИЕ N 21 сообщить об ошибке
ЗАДАНИЕ N 21 сообщить об ошибке
Тема: Основные методы интегрирования
Множество первообразных функции  имеет вид :
имеет вид :
Решение:
Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции. Тогда
Произведем замену  ,
,  ,
,  :
:
.
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191832[05.04.2012 23:43:09]
 ЗАДАНИЕ N 22 сообщить об ошибке
ЗАДАНИЕ N 22 сообщить об ошибке
Тема: Дифференциальное исчисление ФНП
Частная производная  функции
функции  имеет вид :
имеет вид :
Решение:
При вычислении частной производной |
по переменной , переменную рассматриваем |
как постоянную величину. Тогда |
|
|
. |
 ЗАДАНИЕ N 23 сообщить об ошибке
ЗАДАНИЕ N 23 сообщить об ошибке
Тема: Область определения функции
Область определения функции  имеет вид :
имеет вид :
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191832[05.04.2012 23:43:09]
Решение:
Данная функция определена, если определен |
|
, то есть |
, и подкоренное |
выражение в знаменателе положительно, то есть |
|
|
. Решив неравенство |
, получаем |
. Для решения неравенства |
|
|
найдем предварительно |
корни уравнения |
|
, а именно |
и |
. Тогда методом интервалов |
можем получить, что |
|
. Следовательно, область определения данной |
функции будет иметь вид |
. |
|
|
|
 ЗАДАНИЕ N 24 сообщить об ошибке
ЗАДАНИЕ N 24 сообщить об ошибке
Тема: Предел функции
Предел  равен :
равен :
4
1
 ЗАДАНИЕ N 25 сообщить об ошибке
ЗАДАНИЕ N 25 сообщить об ошибке
Тема: Производные первого порядка
Производная функции  равна :
равна :
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191832[05.04.2012 23:43:09]



 и
и  могут принимать значения :
могут принимать значения : ,
, 
 ,
, 
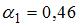 ,
, 
 ,
, 
 ЗАДАНИЕ N 13 сообщить об ошибке
ЗАДАНИЕ N 13 сообщить об ошибке . Тогда функции спроса
. Тогда функции спроса  и предложения
и предложения  могут иметь вид :
могут иметь вид :




 ЗАДАНИЕ N 19 сообщить об ошибке
ЗАДАНИЕ N 19 сообщить об ошибке ЗАДАНИЕ N 20 сообщить об ошибке
ЗАДАНИЕ N 20 сообщить об ошибке задается уравнением вида :
задается уравнением вида :


 ЗАДАНИЕ N 24 сообщить об ошибке
ЗАДАНИЕ N 24 сообщить об ошибке равен :
равен : ЗАДАНИЕ N 25 сообщить об ошибке
ЗАДАНИЕ N 25 сообщить об ошибке равна :
равна :


 равно :
равно :
 ,
, 
 ,
, 
 ,
, 
 ,
, 

 равно :
равно :

 имеет задача B
имеет задача B имеет задача A
имеет задача A имеет и задача A и задача B
имеет и задача A и задача B  не имеет ни одна из задач
не имеет ни одна из задач . То
. То
 . Тогда значение параметра
. Тогда значение параметра 

 , или соответственно
, или соответственно .
.
 имеет вид :
имеет вид : ,
,  ,
, 

 функции
функции  имеет вид :
имеет вид :
 имеет вид :
имеет вид :