Решение:
Если выразить матрицу  , то получим равенство:
, то получим равенство:  .
.
 ЗАДАНИЕ N 24 сообщить об ошибке
ЗАДАНИЕ N 24 сообщить об ошибке
Тема: Ранг матрицы
Ранг матрицы  равен двум, если значение
равен двум, если значение  не равно :
не равно :
- 1 0 - 2 1
Решение:
Рангом матрицы называется наибольший из порядков ее миноров, не равных нулю. Следовательно, если минор второго порядка не равен нулю, то ранг будет равен двум.
Вычислим  . То есть
. То есть  .
.
 ЗАДАНИЕ N 25 сообщить об ошибке
ЗАДАНИЕ N 25 сообщить об ошибке
Тема: Предел функции
Предел  равен :
равен :
0
1
Решение:
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191831[05.04.2012 23:49:30]
Для раскрытия этой неопределенности умножим числитель и знаменатель на выражение, сопряженное числителю, то есть на  :
:
ЗАДАНИЕ N 26 сообщить об ошибке |
|
|
Тема: Дифференциальное исчисление ФНП |
|
|
Приближенное значение функции |
в точке |
, |
вычисленное с помощью полного дифференциала, равно : |
|
|
Решение:
Воспользуемся формулой |
|
, |
где |
, |
, |
, |
. |
Вычислим последовательно |
; |
|
|
|
|
|
|
|
|
, |
; |
|
|
|
, |
. |
Тогда |
|
|
|
. |
|
|
|
|
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191831[05.04.2012 23:49:30]
 ЗАДАНИЕ N 27 сообщить об ошибке
ЗАДАНИЕ N 27 сообщить об ошибке
Тема: Приложения дифференциального исчисления ФОП
Наибольшее значение функции на отрезке
на отрезке  равно :
равно :
- 1
0
Решение:
Вычислим производную первого порядка |
|
и решим |
уравнение |
, а именно |
. Тогда |
. Так как |
|
, а |
, то вычислим |
|
|
, |
, |
. Тогда наибольшее значение данной функции |
равно |
. |
|
|
|
 ЗАДАНИЕ N 28 сообщить об ошибке
ЗАДАНИЕ N 28 сообщить об ошибке
Тема: Производные первого порядка
Производная функции  равна :
равна :
Решение:
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191831[05.04.2012 23:49:30]
 ЗАДАНИЕ N 29 сообщить об ошибке
ЗАДАНИЕ N 29 сообщить об ошибке
Тема: Свойства определенного интеграла
Среднее значение функции  на отрезке
на отрезке 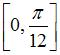 равно :
равно :
Решение:
Среднее значение функции 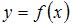 , непрерывной на отрезке
, непрерывной на отрезке  , вычисляется по формуле
, вычисляется по формуле
, где 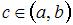 . Тогда
. Тогда
.
 ЗАДАНИЕ N 30 сообщить об ошибке
ЗАДАНИЕ N 30 сообщить об ошибке
Тема: Асимптоты графика функции
Вертикальная асимптота графика функции  задается уравнением вида :
задается уравнением вида :
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191831[05.04.2012 23:49:30]
Решение:
|
|
|
|
Прямая |
является вертикальной асимптотой графика функции |
, если эта |
функция определена в некоторой окрестности точки |
и |
, или |
. Вертикальные асимптоты обычно сопутствуют точкам разрыва второго рода. Определим точки разрыва данной функции. Это точки, в которых знаменатель равен
нулю. То есть |
, или |
, |
. |
|
|
Вычислим односторонние пределы функции |
|
в точке |
: |
|
|
|
|
|
. |
Аналогично и |
|
, то есть прямая |
не является вертикальной |
асимптотой. |
|
|
|
в точке |
: |
Вычислим односторонние пределы функции |
|
,
.
Следовательно, прямая  будет вертикальной асимптотой.
будет вертикальной асимптотой.
 ЗАДАНИЕ N 31 сообщить об ошибке
ЗАДАНИЕ N 31 сообщить об ошибке
Тема: Область определения функции
Область определения функции  имеет вид :
имеет вид :
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191831[05.04.2012 23:49:30]
Решение:
Область определения данной функции определяется как решение системы неравенств:
то есть  .
.
 ЗАДАНИЕ N 32 сообщить об ошибке
ЗАДАНИЕ N 32 сообщить об ошибке
Тема: Основные методы интегрирования
Множество первообразных функции  имеет вид :
имеет вид :
Решение:
Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции методом интегрирования по частям по формуле  . Тогда
. Тогда
.
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191831[05.04.2012 23:49:30]
Преподаватель: Базайкина О.Л.
Специальность: 080104.65 - Экономика труда
Группа: ЭЭТ-092 Дисциплина: Математика
Идентификатор студента: Захарова М.
Логин: 05ps191832
Начало тестирования: 2012-04-04 14:37:03 Завершение тестирования: 2012-04-04 15:35:36 Продолжительность тестирования: 58 мин. Заданий в тесте: 32 Кол-во правильно выполненных заданий: 18
Процент правильно выполненных заданий: 56 %
 ЗАДАНИЕ N 1 сообщить об ошибке
ЗАДАНИЕ N 1 сообщить об ошибке
Тема: Теоремы сложения и умножения вероятностей
Из урны, в которой лежат 3 белых и 7 черных шара, наудачу по одному извлекают два шара без возвращения. Тогда вероятность того, что только один из извлеченных шаров будет белым, равна
:
Решение:
Введем обозначения событий: - k-ый вынутый шар будет белым, A - только один из
извлеченных шаров будет белым. Тогда |
, и так как по условию задачи |
события |
и |
зависимы, то |
|
.
 ЗАДАНИЕ N 2 сообщить об ошибке
ЗАДАНИЕ N 2 сообщить об ошибке
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191832[05.04.2012 23:43:09]
Тема: Определение вероятности
При наборе телефонного номера абонент забыл две последние цифры и набрал их наудачу, помня только, что эти цифры нечетные и разные. Тогда вероятность того, что номер набран правильно, равна :
 ЗАДАНИЕ N 3 сообщить об ошибке
ЗАДАНИЕ N 3 сообщить об ошибке
Тема: Числовые характеристики случайных величин
Непрерывная случайная величина |
задана плотностью распределения вероятностей |
. Тогда математическое ожидание a и среднее квадратическое отклонение
этой случайной величины равны :
 ЗАДАНИЕ N 4 сообщить об ошибке
ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Законы распределения вероятностей дискретных случайных величин
Банк выдал пять кредитов. Вероятность того, что кредит не будет погашен в срок, равна 0,1. Тогда вероятность того, что в срок не будут погашены три кредита, равна :
0,0081
0,081
0,06
0,0729
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191832[05.04.2012 23:43:09]
Решение:
Воспользуемся формулой Бернулли: |
|
|
|
, где |
, |
, |
, |
. |
Тогда |
|
|
|
. |
ЗАДАНИЕ N 5 сообщить об ошибке |
|
|
Тема: Элементы корреляционного анализа |
|
|
Выборочное уравнение прямой линии регрессии |
на имеет вид |
. Тогда |
выборочный коэффициент корреляции может быть равен :
 ЗАДАНИЕ N 6 сообщить об ошибке
ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Точечные оценки параметров распределения
Если все варианты |
исходного вариационного ряда увеличить в два раза, то выборочная |
дисперсия |
: |
|

 увеличится в четыре раза
увеличится в четыре раза
 увеличится в два раза
увеличится в два раза
 не изменится
не изменится  увеличится на четыре единицы
увеличится на четыре единицы
Решение:
Для исходного вариационного ряда выборочную дисперсию можем вычислить по формуле
.
Тогда для нового вариационного ряда
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191832[05.04.2012 23:43:09]
,
то есть увеличится в четыре раза.
ЗАДАНИЕ N 7 сообщить об ошибке |
|
Тема: Проверка статистических гипотез |
|
Для проверки нулевой гипотезы |
при заданном уровне значимости |
выдвинута конкурирующая гипотеза |
. Тогда область принятия гипотезы может |
иметь вид : |
|
 ЗАДАНИЕ N 8 сообщить об ошибке
ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Статистическое распределение выборки
Статистическое распределение выборки имеет вид
Тогда значение относительной частоты  равно :
равно :
0,25
0,05
0,26
0,75
Решение:
Сумма относительных частот равна единице. Поэтому
.
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191832[05.04.2012 23:43:09]


 , то получим равенство:
, то получим равенство:  .
. ЗАДАНИЕ N 24 сообщить об ошибке
ЗАДАНИЕ N 24 сообщить об ошибке равен двум, если значение
равен двум, если значение  не равно :
не равно : . То есть
. То есть  .
. ЗАДАНИЕ N 25 сообщить об ошибке
ЗАДАНИЕ N 25 сообщить об ошибке равен :
равен :



 будет вертикальной асимптотой.
будет вертикальной асимптотой. ЗАДАНИЕ N 31 сообщить об ошибке
ЗАДАНИЕ N 31 сообщить об ошибке имеет вид :
имеет вид :







 на отрезке
на отрезке  равно :
равно :
 равна :
равна :
 на отрезке
на отрезке 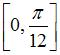 равно :
равно :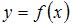 , непрерывной на отрезке
, непрерывной на отрезке  , вычисляется по формуле
, вычисляется по формуле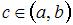 . Тогда
. Тогда
 задается уравнением вида :
задается уравнением вида : .
.
 имеет вид :
имеет вид : . Тогда
. Тогда





 увеличится в четыре раза
увеличится в четыре раза увеличится в два раза
увеличится в два раза не изменится
не изменится  увеличится на четыре единицы
увеличится на четыре единицы
 равно :
равно :