Решение:
Для вычисления события (среди отобранных деталей нет годных) воспользуемся формулой , где n - общее число возможных элементарных исходов испытания, а m - число
элементарных исходов, благоприятствующих появлению события . В нашем случае общее
число возможных элементарных исходов равно числу способов, которыми можно извлечь три детали из 12 имеющих, то есть . А общее число благоприятствующих исходов равно
числу способов, которыми можно извлечь три бракованные детали из пяти, то есть  .
.
Следовательно,
 ЗАДАНИЕ N 9 сообщить об ошибке
ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Законы распределения вероятностей дискретных случайных величин
Дискретная случайная величина  задана функцией распределения вероятностей
задана функцией распределения вероятностей
Тогда вероятность |
равна : |
0,54 |
|
0,38 |
|
0,70 |
|
0,86 |
|
Решение:
Так как по определению  , то случайную величину можно задать
, то случайную величину можно задать
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191831[05.04.2012 23:49:30]
законом распределения вероятностей вида
Следовательно,  .
.
 ЗАДАНИЕ N 10 сообщить об ошибке
ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Числовые характеристики случайных величин
Проводится n независимых испытаний, в каждом из которых вероятность появления события A постоянна и равна 0,6. Тогда математическое ожидание и дисперсия дискретной
случайной величины X - числа появлений события A в  проведенных испытаниях равны :
проведенных испытаниях равны :
 ,
, 
 ,
, 
 ,
, 
 ,
, 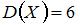
Решение:
Случайная величина X подчиняется биномиальному закону распределения вероятностей. Поэтому  , а
, а  .
.
 ЗАДАНИЕ N 11 сообщить об ошибке
ЗАДАНИЕ N 11 сообщить об ошибке
Тема: Функции полезности
Функция полезности потребителя имеет вид |
, а оптимальное потребление: |
, |
 . Тогда предельная полезность блага
. Тогда предельная полезность блага  равна :
равна :
0,8
6,25
0,16
1,25
 ЗАДАНИЕ N 12 сообщить об ошибке
ЗАДАНИЕ N 12 сообщить об ошибке
Тема: Сетевое планирование и управление
Объемы промежуточной продукции в линейной статической модели Леонтьева представлены
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191831[05.04.2012 23:49:30]
матрицей |
, а объемы валовых выпусков - вектором |
. Тогда объемы конечного |
продукта будут представлены вектором :
Решение:
В модели Леонтьева валовой выпуск , конечный продукт и промежуточное потребление связаны системой уравнений:
Тогда
 ЗАДАНИЕ N 13 сообщить об ошибке
ЗАДАНИЕ N 13 сообщить об ошибке
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191831[05.04.2012 23:49:30]
Тема: Функции спроса и предложения |
|
Даны функции спроса |
и предложения |
, где - цена товара. Тогда |
равновесная цена спроса-предложения равна : |
|
2 |
|
|
3
 ЗАДАНИЕ N 14 сообщить об ошибке
ЗАДАНИЕ N 14 сообщить об ошибке
Тема: Производственные функции
Неоклассическая производственная функция вида  не обладает свойством :
не обладает свойством :
Решение:
Неоклассическая производственная функция вида  обладает свойством
обладает свойством
, так как с ростом ресурсов выпуск растет;
обладает свойством |
, так как при отсутствии одного из ресурсов |
производство невозможно; |
, так как при неограниченном увеличении |
обладает свойством |
одного из ресурсов выпуск неограниченно возрастает.
Инеоклассическая производственная функция вида  не обладает свойством
не обладает свойством
,так как с увеличением ресурсов скорость роста выпуска замедляется, то
есть
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191831[05.04.2012 23:49:30]
 ЗАДАНИЕ N 15 сообщить об ошибке
ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Транспортная задача
Транспортная задача, заданная распределительной таблицей, имеет вид
Тогда первоначальное распределение поставок, осуществленное по методу <учета наименьших затрат> будет иметь вид :
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191831[05.04.2012 23:49:30]

Решение:
Метод <учета наименьших затрат> означает, что поставка всегда осуществляется в клетку с наименьшим тарифом. Первоначально поставку осуществляем в клетку с номером c
наименьшим значением тарифа, равным 1: выбираем наименьшее значение между мощностью поставщика и потребностью потребителя, то есть . Первому потребителю
больше везти не требуется, поэтому остальные клетки в столбце будут пустые, а у поставщика
|
|
|
|
|
|
осталось 14 - 10=4 единиц товара. Следующая клетка с номером |
(тариф равен 2): |
|
. От первого поставщику больше перевезти нельзя, |
поэтому клетка |
пустая, |
|
у третьего потребителя осталось потребность в 7 - 5=2 единицы товара. Следующая клетка |
|
(тариф равен 3): |
, клетка |
пустая, 12 - 4=8. Далее идет клетка |
|
(тариф равен 4): |
, 10-8=2. И последняя поставка осуществляется в клетку |
: |
. Следовательно, первоначальное распределение будет иметь вид:
 ЗАДАНИЕ N 16 сообщить об ошибке
ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Теория игр: игры с природой
Матрица рисков в игре с природой имеет вид:
Тогда средний риск игрока по критерию Байеса относительно рисков будет равен :
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191831[05.04.2012 23:49:30]
2,4
5
2
4,6
Решение:
Определим предварительно неизвестную вероятность |
и вычислим средние |
риски игрока: |
|
, |
|
, |
|
, |
|
. |
|
Тогда наименьший средний риск игрока будет равен 2,4. |
|
 ЗАДАНИЕ N 17 сообщить об ошибке
ЗАДАНИЕ N 17 сообщить об ошибке
Тема: Линейное программирование: графическое задание области допустимых решений
Область допустимых решений ABCD задачи линейного программирования имеет вид:
Тогда функция  достигает максимального значения :
достигает максимального значения :

 на отрезке AB
на отрезке AB
 на отрезке CD
на отрезке CD
 в точке D
в точке D  только в точке B
только в точке B
Решение:
Построим линию уровня  и градиент целевой функции
и градиент целевой функции
. Тогда целевая функция будет принимать наибольшее значение
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191831[05.04.2012 23:49:30]
в точках <выхода> линии уровня из области допустимых решений в направлении градиента.
|
|
|
Из рисунка видно, что точки максимума будут лежать на отрезке |
как на точках <выхода> |
линии уровня |
из области допустимых решений в направлении градиента. |
 ЗАДАНИЕ N 18 сообщить об ошибке
ЗАДАНИЕ N 18 сообщить об ошибке
Тема: Сетевое планирование и управление
Для сетевого графика, изображенного на рисунке,
длина критического пути равна 58. Тогда значение параметра может быть равно :
18
45
39
20
 ЗАДАНИЕ N 19 сообщить об ошибке
ЗАДАНИЕ N 19 сообщить об ошибке
Тема: Обратная матрица
Даны матрицы  и
и  . Тогда решение матричного уравнения
. Тогда решение матричного уравнения 
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191831[05.04.2012 23:49:30]
имеет вид :
Решение:
Решение матричного уравнения имеет вид: , где
, где
 - обратная матрица.
- обратная матрица.
Вычислим последовательно
Тогда Следовательно
 ЗАДАНИЕ N 20 сообщить об ошибке
ЗАДАНИЕ N 20 сообщить об ошибке
Тема: Определение линейного пространства
Аксиомой линейного пространства  не является :
не является :
 ,
, 
 ,
, 
 ,
, 
 ,
, 
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191831[05.04.2012 23:49:30]
 ЗАДАНИЕ N 21 сообщить об ошибке
ЗАДАНИЕ N 21 сообщить об ошибке
Тема: Системы линейных уравнений
Система  не имеет решений, если
не имеет решений, если  равно :
равно :
- 2 2 1 0
 ЗАДАНИЕ N 22 сообщить об ошибке
ЗАДАНИЕ N 22 сообщить об ошибке
Тема: Вычисление определителей
Определитель  равен :
равен :
ЗАДАНИЕ N 23 сообщить об ошибке |
|
Тема: Линейные операции над матрицами |
|
Матрицы |
имеют одинаковую размерность. Если - единичная матрица того же размера, |
что и матрицы |
, и матрица |
, тогда верно равенство : |
http://mypage.i-exam.ru/index.php?menu=show_test&login=05ps191831[05.04.2012 23:49:30]


 .
. ЗАДАНИЕ N 9 сообщить об ошибке
ЗАДАНИЕ N 9 сообщить об ошибке задана функцией распределения вероятностей
задана функцией распределения вероятностей , то случайную величину можно задать
, то случайную величину можно задать









 .
.
 проведенных испытаниях равны :
проведенных испытаниях равны : ,
, 
 ,
, 
 ,
, 
 ,
, 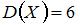
 , а
, а  .
.
 . Тогда предельная полезность блага
. Тогда предельная полезность блага  равна :
равна :



 обладает свойством
обладает свойством не обладает свойством
не обладает свойством


 достигает максимального значения :
достигает максимального значения :
 на отрезке AB
на отрезке AB на отрезке CD
на отрезке CD в точке D
в точке D  только в точке B
только в точке B и градиент целевой функции
и градиент целевой функции

 и
и  . Тогда решение матричного уравнения
. Тогда решение матричного уравнения 
 , где
, где - обратная матрица.
- обратная матрица.

 ,
, 
 ,
, 
 ,
, 
 ,
, 

 не имеет решений, если
не имеет решений, если  равно :
равно :
 равен :
равен :