
3
.pdf
Решение:
Обратная матрица имеет вид  , вычислим
, вычислим
 Получается, что
Получается, что

 ЗАДАНИЕ N 15 сообщить об ошибке
ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Системы линейных уравнений
Единственное решение имеет однородная система линейных уравнений …

Решение:
Однородная система линейных алгебраических уравнений имеет одно единственное решение, если ее определитель не равен нулю.
1. Из системы  , получим
, получим 
 ,
,
следовательно, система имеет единственное решение.
2.Из системы 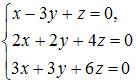 , получим
, получим  , так как последние две строки пропорциональны.
, так как последние две строки пропорциональны.
3.Из системы  , получим
, получим  , так как последние две строки пропорциональны.
, так как последние две строки пропорциональны.
4.Из системы  , получим
, получим  , так как первый и третий столбцы пропорциональны.
, так как первый и третий столбцы пропорциональны.
 ЗАДАНИЕ N 16 сообщить об ошибке
ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Ранг матрицы
Ранг матрицы  равен двум, если значение
равен двум, если значение  не равно …
не равно …
– 1

0
– 2
1

 ЗАДАНИЕ N 17 сообщить об ошибке
ЗАДАНИЕ N 17 сообщить об ошибке
Тема: Определение линейного пространства
Среди представленных множеств линейное пространство образует …
множество всех комплексных чисел
множество всех натуральных чисел
множество всех положительных иррациональных чисел
множество всех отрицательных рациональных чисел
Решение:
Множество  образует линейное пространство, если для любых 2-х его
образует линейное пространство, если для любых 2-х его
элементов 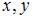 определены операции сложения
определены операции сложения  и умножения на действительное число
и умножения на действительное число  ;
;  со свойствами:
со свойствами:


Наладчик обслуживает три станка. Вероятность того, что в течение часа потребует его вмешательства первый станок, равна  ; второй –
; второй –  ; третий
; третий
–  . Тогда вероятность того, что в течение часа потребует вмешательства наладчика хотя бы один станок, равна …
. Тогда вероятность того, что в течение часа потребует вмешательства наладчика хотя бы один станок, равна …
0,49
0,51
0,6
0,25
Решение:
Введем обозначения событий: (вмешательства наладчика потребует
(вмешательства наладчика потребует  – ый
– ый
станок),  (вмешательства наладчика потребует хотя бы один станок). Тогда
(вмешательства наладчика потребует хотя бы один станок). Тогда
.

 ЗАДАНИЕ N 20 сообщить об ошибке
ЗАДАНИЕ N 20 сообщить об ошибке
Тема: Законы распределения вероятностей дискретных случайных величин
Банк выдал пять кредитов. Вероятность того, что кредит не будет погашен в срок, равна 0,1. Тогда вероятность того, что в срок не будут погашены три кредита, равна …
0,0081

0,081
0,06
0,0729
Решение:
Воспользуемся формулой Бернулли:  , где
, где  ,
, 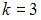 ,
,  ,
,  .
.
Тогда  .
.

 ЗАДАНИЕ N 21 сообщить об ошибке
ЗАДАНИЕ N 21 сообщить об ошибке
Тема: Определение вероятности
В партии из 12 деталей имеется 5 бракованных. Наудачу отобраны три детали. Тогда вероятность того, что среди отобранных деталей нет бракованных, равна
…

Решение:
Для вычисления события  (среди отобранных деталей нет бракованных)
(среди отобранных деталей нет бракованных)
воспользуемся формулой  , где n – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события
, где n – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события  . В нашем случае общее число возможных элементарных исходов равно числу способов, которыми можно
. В нашем случае общее число возможных элементарных исходов равно числу способов, которыми можно
извлечь три детали из 12 имеющих, то есть  . А общее число благоприятствующих исходов равно числу способов, которыми можно извлечь
. А общее число благоприятствующих исходов равно числу способов, которыми можно извлечь
три небракованные детали из семи, то есть  . Следовательно,
. Следовательно,

 ЗАДАНИЕ N 22 сообщить об ошибке
ЗАДАНИЕ N 22 сообщить об ошибке
Тема: Числовые характеристики случайных величин
Непрерывная случайная величина  задана плотностью распределения
задана плотностью распределения
вероятностей  . Тогда математическое ожидание a и среднее квадратическое отклонение
. Тогда математическое ожидание a и среднее квадратическое отклонение  этой случайной величины равны …
этой случайной величины равны …

Решение:
Плотность распределения вероятностей нормально распределенной случайной
величины  имеет вид
имеет вид  , где
, где  ,
,  . Поэтому
. Поэтому  .
.

 ЗАДАНИЕ N 23 сообщить об ошибке
ЗАДАНИЕ N 23 сообщить об ошибке
Тема: Точечные оценки параметров распределения
В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 15; 18; 21; 24. Тогда выборочная дисперсия равна …
11,25
19,5
15
21,25

Решение:
Выборочная дисперсия вычисляется по формуле
 , где
, где  . Вычислив предварительно
. Вычислив предварительно
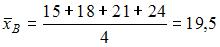 , получаем
, получаем
.

 ЗАДАНИЕ N 24 сообщить об ошибке
ЗАДАНИЕ N 24 сообщить об ошибке
Тема: Интервальные оценки параметров распределения
Дан доверительный интервал 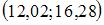 для оценки математического ожидания нормально распределенного количественного признака. Тогда при уменьшении объема выборки этот доверительный интервал может принять вид
для оценки математического ожидания нормально распределенного количественного признака. Тогда при уменьшении объема выборки этот доверительный интервал может принять вид
…
Решение:
Доверительный интервал для оценки математического ожидания нормально распределенного количественного признака можно представить в виде
симметричного интервала  , где точечная оценка
, где точечная оценка









 и
и  . Если
. Если 
 равен …
равен …

 , а точность оценки
, а точность оценки 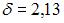 . В случае
. В случае будет больше 2,13.
будет больше 2,13.

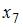 , 12, 13, 15, 16, 18 равна 10. Тогда значение варианты
, 12, 13, 15, 16, 18 равна 10. Тогда значение варианты  равно …
равно … , то медиана равна их средней арифметической, то есть
, то медиана равна их средней арифметической, то есть  . Тогда
. Тогда  .
.

 , полигон частот которой имеет вид:
, полигон частот которой имеет вид: