3

равен разности между и наибольшей длиной () пути, проходящей через эту работу. Следовательно, .

ЗАДАНИЕ N 10 сообщить об ошибке

Тема: Теория игр: игры с природой

Матрица выигрышей в игре с природой имеет вид:

Тогда оптимальной по критерию Байеса относительно выигрышей будет стратегия …

ЗАДАНИЕ N 11 сообщить об ошибке

Тема: Элементы корреляционного анализа

Выборочное уравнение прямой линии регрессии на имеет вид

. Тогда выборочное среднее признака равно …

ЗАДАНИЕ N 12 сообщить об ошибке

Тема: Проверка статистических гипотез

Двусторонняя критическая область может определяться из соотношения …

ЗАДАНИЕ N 13 сообщить об ошибке

Тема: Интервальные оценки параметров распределения

Точечная оценка математического ожидания нормально распределенного количественного признака равна 12,04. Тогда его интервальная оценка с точностью 1,66 имеет вид …

ЗАДАНИЕ N 14 сообщить об ошибке

Тема: Статистическое распределение выборки

Из генеральной совокупности извлечена выборка объема :

Тогда значение равно …

34

81

Медиана вариационного ряда 11, 13, 13, 14, 15, , 18, 19, 21, 24, 25, 25 равна

17. Тогда значение варианты равно …

16

17

18

15

ЗАДАНИЕ N 17 сообщить об ошибке

Тема: Основные методы интегрирования

Множество первообразных функции имеет вид …

Решение:

Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции методом интегрирования по частям по формуле

. Тогда

.

ЗАДАНИЕ N 18 сообщить об ошибке

Тема: Производные первого порядка

Производная функции равна …

ЗАДАНИЕ N 19 сообщить об ошибке

Тема: Дифференциальное исчисление ФНП

Частная производная функции имеет вид …

Решение:

При вычислении частной производной по переменной , переменную рассматриваем как постоянную величину. Тогда

.

ЗАДАНИЕ N 20 сообщить об ошибке

Тема: Область определения функции

Область определения функции имеет вид …

Решение:

Данная функция определена, если . Возведем обе части этого

неравенства в квадрат и получим , или . Решив последнее неравенство, например, методом интервалов, получаем:

.

ЗАДАНИЕ N 21 сообщить об ошибке

Тема: Предел функции

Предел равен …

0

1

Решение:

Для раскрытия этой неопределенности умножим числитель и знаменатель на выражение, сопряженное числителю, то есть на :

ЗАДАНИЕ N 22 сообщить об ошибке

Тема: Свойства определенного интеграла

Если функция непрерывна на отрезке , то интеграл можно представить в виде …

Решение:

Если функция непрерывна на отрезке и 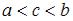, то справедливо следующее свойство определенного интеграла:

.

Тогда .

ЗАДАНИЕ N 23 сообщить об ошибке

Тема: Асимптоты графика функции

Наклонная асимптота графика функции задается уравнением вида …