3

для любого может существовать несколько противоположных элементов

для любого

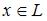
может существует несколько нейтральных элементов

ЗАДАНИЕ N 21 сообщить об ошибке

Тема: Обратная матрица

Для матрицы не существует обратной, если равно …

ЗАДАНИЕ N 22 сообщить об ошибке

Тема: Ранг матрицы

Ранг матрицы равен …

2

1

3

4

Решение:

Рангом матрицы называется наибольший из порядков ее миноров, не равных нулю. Существуют ненулевые миноры второго порядка, например:

.

Следовательно, ранг равен двум.

ЗАДАНИЕ N 23 сообщить об ошибке

Тема: Проверка статистических гипотез

Основная гипотеза имеет вид 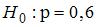. Тогда конкурирующей может являться гипотеза …

ЗАДАНИЕ N 24 сообщить об ошибке

Тема: Точечные оценки параметров распределения

Проведено пять измерений (без систематических ошибок) некоторой случайной величины (в мм): 4,5; 5,2; 6,1; 7,8, 8,3. Тогда несмещенная оценка математического ожидания равна …

6,38

6,42

6,1

6,4

ЗАДАНИЕ N 25 сообщить об ошибке

Тема: Интервальные оценки параметров распределения

Точечная оценка математического ожидания нормально распределенного количественного признака равна 12,04. Тогда его интервальная оценка с точностью 1,66 имеет вид …

ЗАДАНИЕ N 26 сообщить об ошибке

Тема: Характеристики вариационного ряда

Размах варьирования вариационного ряда –1, 0, 2, 3, 4, 5, 7, 8, 10, 12, 14 равен …

15

13

5

11

ЗАДАНИЕ N 27 сообщить об ошибке

Тема: Элементы корреляционного анализа

Выборочное уравнение прямой линии регрессии на имеет вид

. Тогда выборочный коэффициент корреляции может быть равен …

ЗАДАНИЕ N 28 сообщить об ошибке

Тема: Статистическое распределение выборки

Из генеральной совокупности извлечена выборка объема , полигон частот которой имеет вид:

Тогда число вариант в выборке равно …

32

Тогда минимальное значение функции достигается в точке …

B

О

C

D

ЗАДАНИЕ N 31 сообщить об ошибке

Тема: Транспортная задача

В транспортных задачах

A)

B)

оптимальное распределение поставок …

имеет задача B имеет задача A

имеет и задача A и задача B не имеет ни одна из задач

ЗАДАНИЕ N 32 сообщить об ошибке

Тема: Сетевое планирование и управление

Сетевой график изображен на рисунке

0

4

34

20

Решение:

Выделим полные пути: , , , ,

вычислим их длины: , , , . Тогда критическим будет путь с

наибольшей длиной . Так как работа располагается на критическом пути, то ее резервы равны нулю, то есть .

Точечная оценка вероятности биномиально распределенного количественного признака равна 0,38. Тогда его интервальная оценка может иметь вид …

Решение:

Интервальная оценка вероятности биномиально распределенного количественного признака симметрична относительно его точечной оценки, и

. Таким свойствам удовлетворяет интервал .

ЗАДАНИЕ N 4 сообщить об ошибке

Тема: Проверка статистических гипотез

Соотношением вида можно определить …

левостороннюю критическую область правостороннюю критическую область

двустороннюю критическую область область принятия гипотезы

Решение:

Данное соотношение определяет левостороннюю критическую область, так как левосторонней называют критическую область, определяемую соотношением

, где – положительное число, а – уровень значимости.

ЗАДАНИЕ N 5 сообщить об ошибке

Тема: Статистическое распределение выборки

Из генеральной совокупности извлечена выборка объема :

Тогда значение равно …

34

81

47

33

Решение:

Объем выборки вычисляется по формуле , где – частота варианты

. Тогда .

ЗАДАНИЕ N 6 сообщить об ошибке

Тема: Точечные оценки параметров распределения

В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 15; 18; 21; 24. Тогда выборочная дисперсия равна …

11,25

19,5

15

21,25

Решение:

Выборочная дисперсия вычисляется по формуле

, где . Вычислив предварительно

, получаем

.

ЗАДАНИЕ N 7 сообщить об ошибке

Тема: Транспортная задача