
3
.pdf
обладает свойством  , так как при неограниченном увеличении одного из ресурсов выпуск неограниченно возрастает.
, так как при неограниченном увеличении одного из ресурсов выпуск неограниченно возрастает.
И неоклассическая производственная функция вида 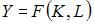 не обладает свойством
не обладает свойством  , так как с увеличением ресурсов скорость роста выпуска замедляется, то есть
, так как с увеличением ресурсов скорость роста выпуска замедляется, то есть 

 ЗАДАНИЕ N 19 сообщить об ошибке
ЗАДАНИЕ N 19 сообщить об ошибке
Тема: Основные методы интегрирования
Множество первообразных функции  имеет вид …
имеет вид …
Решение:
Чтобы определить множество первообразных, вычислим неопределенный интеграл от этой функции. Тогда
Произведем замену  ,
,  ,
,  :
:
.

 ЗАДАНИЕ N 20 сообщить об ошибке
ЗАДАНИЕ N 20 сообщить об ошибке
Тема: Дифференциальное исчисление ФНП
Приближенное значение функции  в точке
в точке  , вычисленное с помощью полного дифференциала, равно …
, вычисленное с помощью полного дифференциала, равно …

Решение:
Воспользуемся формулой
 ,
,
где  ,
,  ,
,  ,
,  .
.
Вычислим последовательно
 ;
;
 ,
,  ;
;
 ,
,  .
.
Тогда
.

 ЗАДАНИЕ N 21 сообщить об ошибке
ЗАДАНИЕ N 21 сообщить об ошибке
Тема: Предел функции
Предел  равен …
равен …
Решение:
Для раскрытия этой неопределенности умножим числитель и знаменатель на выражение, сопряженное знаменателю, то есть на  :
:


 ЗАДАНИЕ N 22 сообщить об ошибке
ЗАДАНИЕ N 22 сообщить об ошибке
Тема: Асимптоты графика функции
Наклонная асимптота графика функции  задается уравнением вида …
задается уравнением вида …


 , при
, при 

 , при
, при 

 , при
, при 
 , при
, при 
Решение:
Прямая  является наклонной асимптотой графика функции
является наклонной асимптотой графика функции  при
при  (
( ), если существуют конечные пределы:
), если существуют конечные пределы:
 ,
,  , или, соответственно:
, или, соответственно:
 ,
,  .
.
Вычислим эти пределы:
,
 .
.
Следовательно, прямая  является наклонной асимптотой графика данной функции при
является наклонной асимптотой графика данной функции при  .
.
 ,
,
То есть при  наклонной асимптоты у графика данной функции нет.
наклонной асимптоты у графика данной функции нет.
 ЗАДАНИЕ N 23 сообщить об ошибке
ЗАДАНИЕ N 23 сообщить об ошибке
Тема: Свойства определенного интеграла


Область определения функции  содержит интервал
содержит интервал  . Тогда значение параметра
. Тогда значение параметра  может быть равно …
может быть равно …
0,5
2
1
0
Решение:
Если  , то область определения данной функции определяется как
, то область определения данной функции определяется как
решение системы неравенств:  то есть
то есть  . Если
. Если  , то область определения определяется как решение системы
, то область определения определяется как решение системы
неравенств:  то есть
то есть  . Следовательно,
. Следовательно,  , например,
, например,  .
.

 ЗАДАНИЕ N 26 сообщить об ошибке
ЗАДАНИЕ N 26 сообщить об ошибке
Тема: Производные первого порядка
Производная функции  равна …
равна …


Решение:
Фундаментальное решение может быть вычислено для однородной системы линейных алгебраических уравнений. Однородной системой линейных алгебраических уравнений называется система, все свободные члены которой
равны нулю, например, система 
 ЗАДАНИЕ N 29 сообщить об ошибке
ЗАДАНИЕ N 29 сообщить об ошибке
Тема: Линейные операции над матрицами
Дана матрица  . Тогда матрица
. Тогда матрица  равна …
равна …

 ЗАДАНИЕ N 30 сообщить об ошибке
ЗАДАНИЕ N 30 сообщить об ошибке
Тема: Обратная матрица
Для матрицы 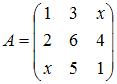 не существует обратной, если значение
не существует обратной, если значение  равно …
равно …
2
– 2 1
– 1

 ЗАДАНИЕ N 31 сообщить об ошибке
ЗАДАНИЕ N 31 сообщить об ошибке
Тема: Ранг матрицы
Ранг матрицы  равен двум, если значение
равен двум, если значение  не равно …
не равно …
– 1 0
– 2 1
Решение:
Рангом матрицы называется наибольший из порядков ее миноров, не равных нулю. Следовательно, если минор второго порядка не равен нулю, то ранг будет
равен двум. Вычислим  . То есть
. То есть  .
.
 ЗАДАНИЕ N 32 сообщить об ошибке
ЗАДАНИЕ N 32 сообщить об ошибке
Тема: Вычисление определителей
Определитель  равен …
равен …
91

97
83
89


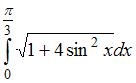 принадлежит промежутку
принадлежит промежутку

 имеет вид …
имеет вид … , то функция
, то функция  в этом промежутке возрастает. Поэтому вычислим производную первого порядка
в этом промежутке возрастает. Поэтому вычислим производную первого порядка  и решим неравенство
и решим неравенство  . Предварительно найдем корни уравнения
. Предварительно найдем корни уравнения  , а именно
, а именно 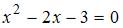 . Тогда
. Тогда  .
. при
при  .
.




 множество всех векторов, принадлежащих пространству
множество всех векторов, принадлежащих пространству 
 , образующих острый угол с положительным направлением оси ординат
, образующих острый угол с положительным направлением оси ординат множество натуральных чисел
множество натуральных чисел множество всех отрицательных вещественных чисел
множество всех отрицательных вещественных чисел образует линейное пространство, если для любых двух его
образует линейное пространство, если для любых двух его определены операции сложения
определены операции сложения 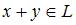 и умножения на действительное число
и умножения на действительное число  ;
;  со свойствами:
со свойствами:





 , образующие острый угол с положительным направлением оси ординат, не образуют линейного пространства, т.к. умножение на отрицательное число делает этот угол тупым; для множество натуральных чисел и множество всех отрицательных вещественных чисел не выполняется шестая аксиома.
, образующие острый угол с положительным направлением оси ординат, не образуют линейного пространства, т.к. умножение на отрицательное число делает этот угол тупым; для множество натуральных чисел и множество всех отрицательных вещественных чисел не выполняется шестая аксиома.



 , а равновесная цена спроса-
, а равновесная цена спроса- . Тогда функции спроса
. Тогда функции спроса  и предложения
и предложения  могут иметь вид …
могут иметь вид … ,
, 
 ,
, 
 ,
, 

 можно взять убывающую функцию, которая проходит через точку с координатами
можно взять убывающую функцию, которая проходит через точку с координатами  ,
,  , а в качестве функции предложения
, а в качестве функции предложения  можно взять возрастающую функцию, которая проходит через точку с таким же координатами
можно взять возрастающую функцию, которая проходит через точку с таким же координатами  ,
,  . Этим условиям
. Этим условиям и
и  .
.
