
3
.pdf
Преподаватель: Базайкина О.Л.
Специальность: 080104.65 - Экономика труда
Группа: ЭЭТ-091 Дисциплина: Математика
Идентификатор студента: Макушенко Р.
Логин: 05ps36351
Начало тестирования: 2012-03-11 10:48:45 Завершение тестирования: 2012-03-11 11:43:34 Продолжительность тестирования: 54 мин. Заданий в тесте: 32 Кол-во правильно выполненных заданий: 9
Процент правильно выполненных заданий: 28 %

 ЗАДАНИЕ N 1 сообщить об ошибке
ЗАДАНИЕ N 1 сообщить об ошибке
Тема: Определение линейного пространства
Линейное пространство  не обладает свойством …
не обладает свойством …
для любого  может существовать несколько противоположных элементов
может существовать несколько противоположных элементов 

 для любого
для любого 

 для любого
для любого 
 нейтральный элемент
нейтральный элемент  является единственным
является единственным
Решение:
Линейное пространство обладает свойствами:
1. Нейтральный элемент  является единственным.
является единственным.
2.  для любого
для любого  .
.
3. Для любого  противоположный элемент
противоположный элемент  является единственным. 4.
является единственным. 4.  для любого
для любого  .
.
5.  для любых
для любых  и
и 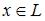 .
.

 ЗАДАНИЕ N 2 сообщить об ошибке
ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Ранг матрицы
Ранг матрицы равен …


 наибольшему из порядков ее миноров, не равных нулю
наибольшему из порядков ее миноров, не равных нулю  наибольшему из ее миноров, не равных нулю
наибольшему из ее миноров, не равных нулю
 числу ненулевых элементов главной диагонали
числу ненулевых элементов главной диагонали  сумме чисел ненулевых элементов главной диагонали
сумме чисел ненулевых элементов главной диагонали


 ЗАДАНИЕ N 3 сообщить об ошибке
ЗАДАНИЕ N 3 сообщить об ошибке
Тема: Вычисление определителей
Корень уравнения  равен …
равен …
– 1
– 5 1 5
 ЗАДАНИЕ N 4 сообщить об ошибке
ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Линейные операции над матрицами
Даны матрицы  и
и  . Тогда решением уравнения
. Тогда решением уравнения  является матрица
является матрица  , равная …
, равная …
 ЗАДАНИЕ N 5 сообщить об ошибке
ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Обратная матрица
Обратной для матрицы  является матрица …
является матрица …


 ЗАДАНИЕ N 6 сообщить об ошибке
ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Системы линейных уравнений
Фундаментальное решение может быть вычислено для системы вида …
Решение:
Фундаментальное решение может быть вычислено для однородной системы линейных алгебраических уравнений. Однородной системой линейных алгебраических уравнений называется система, все свободные члены которой
равны нулю, например, система 

 ЗАДАНИЕ N 7 сообщить об ошибке
ЗАДАНИЕ N 7 сообщить об ошибке
Тема: Статистическое распределение выборки

Из генеральной совокупности извлечена выборка объема  , гистограмма частот которой имеет вид:
, гистограмма частот которой имеет вид:
Тогда значение a равно …
38
39
76
37
Решение:
Так как объем выборки вычисляется как  , где
, где  ,
,
то  .
.

 ЗАДАНИЕ N 8 сообщить об ошибке
ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Точечные оценки параметров распределения
Из генеральной совокупности извлечена выборка объема  :
:
Тогда несмещенная оценка математического ожидания равна …
13,14
13,0
13,34

13,2
Решение:
Несмещенная оценка математического ожидания вычисляется по формуле
 . То есть
. То есть  .
.

 ЗАДАНИЕ N 9 сообщить об ошибке
ЗАДАНИЕ N 9 сообщить об ошибке
Тема: Элементы корреляционного анализа
Выборочное уравнение прямой линии регрессии  на
на  имеет вид
имеет вид
 . Тогда выборочный коэффициент корреляции может быть равен
. Тогда выборочный коэффициент корреляции может быть равен
…
Решение:
Значение выборочного коэффициента корреляции, во-первых, принадлежит промежутку  , а во-вторых, его знак совпадает со знаком выборочного коэффициента регрессии. Этим условиям удовлетворяет значение
, а во-вторых, его знак совпадает со знаком выборочного коэффициента регрессии. Этим условиям удовлетворяет значение  .
.

 ЗАДАНИЕ N 10 сообщить об ошибке
ЗАДАНИЕ N 10 сообщить об ошибке
Тема: Характеристики вариационного ряда
Размах варьирования вариационного ряда 3, 4, 4, 4, 5, 7, 8, 10, 11, 12, 14, 14 равен …
11
4
9
17
Решение:
Размах варьирования вариационного ряда определяется как  , то есть
, то есть  .
.


 ЗАДАНИЕ N 11 сообщить об ошибке
ЗАДАНИЕ N 11 сообщить об ошибке
Тема: Проверка статистических гипотез
Соотношением вида  можно определить …
можно определить …

 правостороннюю критическую область
правостороннюю критическую область  левостороннюю критическую область
левостороннюю критическую область
 двустороннюю критическую область
двустороннюю критическую область  область принятия гипотезы
область принятия гипотезы
Решение:
Данное соотношение определяет правостороннюю критическую область, так как правосторонней называют критическую область, определяемую соотношением
вида  , где
, где  – положительное число, а
– положительное число, а  – уровень значимости.
– уровень значимости.

 ЗАДАНИЕ N 12 сообщить об ошибке
ЗАДАНИЕ N 12 сообщить об ошибке
Тема: Интервальные оценки параметров распределения
Точечная оценка математического ожидания нормально распределенного количественного признака равна 0,4. Тогда его интервальная оценка может иметь вид …
Решение:
Интервальная оценка математического ожидания нормально распределенного количественного признака симметрична относительно его точечной оценки.
Таким свойством обладает интервал  .
.

 ЗАДАНИЕ N 13 сообщить об ошибке
ЗАДАНИЕ N 13 сообщить об ошибке
Тема: Теория игр: игры с природой

Матрица выигрышей в игре с природой имеет вид:
Тогда соответствующая ей матрица рисков будет иметь вид …
Решение:
Определим предварительно показатели благоприятности
 и
и 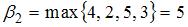 и вычислим соответствующие риски игрока, как разности между показателями благоприятности и соответствующими элементами матрицы выигрышей:
и вычислим соответствующие риски игрока, как разности между показателями благоприятности и соответствующими элементами матрицы выигрышей:

Тема: Линейное программирование: графическое задание области допустимых решений
Область допустимых решений OABC задачи линейного программирования имеет вид:
Тогда максимальное значение функции  достигается в точке …
достигается в точке …
B
D
A
C

 ЗАДАНИЕ N 16 сообщить об ошибке
ЗАДАНИЕ N 16 сообщить об ошибке
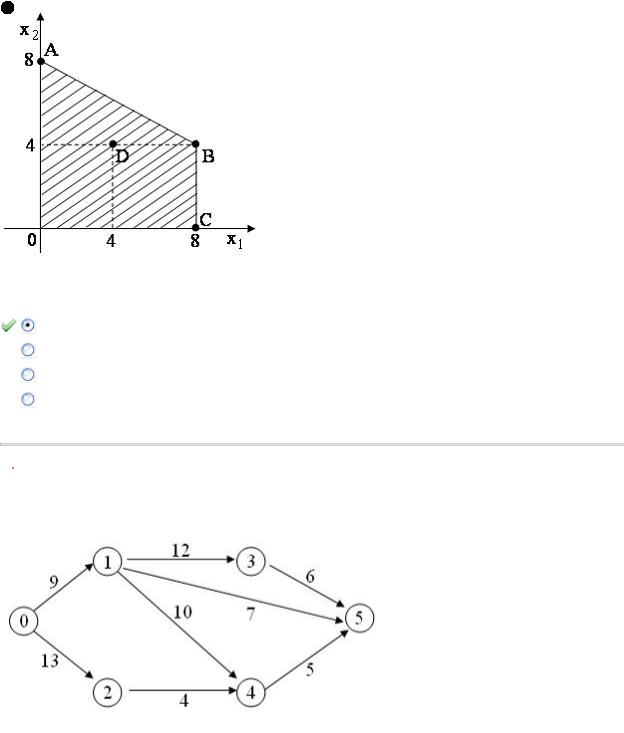
Тема: Сетевое планирование и управление
Для сетевого графика, изображенного на рисунке,
критическими являются работы …


 и
и 

 и
и 

 и
и 


 и
и 
Решение:
Выделим полные пути:  ,
,  ,
,  ,
,  ,
,
вычислим их длины:  ,
,  ,
,
 ,
,  .
.
Критическим путем называется наиболее продолжительный (по времени) полный путь, поэтому это путь  . Тогда критическими будут работы
. Тогда критическими будут работы  ,
,  и
и  .
.

 ЗАДАНИЕ N 17 сообщить об ошибке
ЗАДАНИЕ N 17 сообщить об ошибке
Тема: Дифференциальное исчисление ФНП
Частная производная второго порядка  функции
функции  имеет вид …
имеет вид …
Решение:
При вычислении частной производной функции  по одной из переменных другую переменную рассматриваем как постоянную величину. Тогда
по одной из переменных другую переменную рассматриваем как постоянную величину. Тогда
и
.

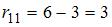 ,
,  ,
,  ,
,  ,
,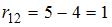 ,
,  ,
,  ,
,  .
.

 будет равно …
будет равно …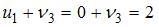 , то есть
, то есть  .
.  , то есть
, то есть  .
. , то есть
, то есть  .
.  , то есть
, то есть  .
.