Тема 6. Кривые второго порядка

Базовый уровень

100. Задние {{1}} тз1

Укажите каноническое уравнение эллипса

R

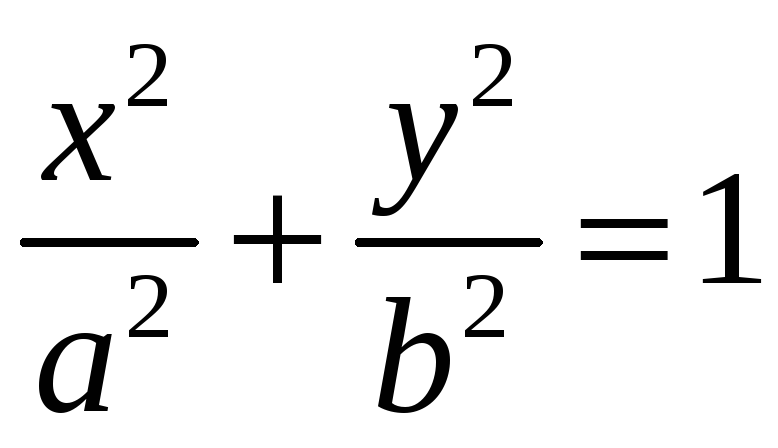
101. Задание {{1}} ТЗ1

Укажите каноническое уравнение гиперболы

R

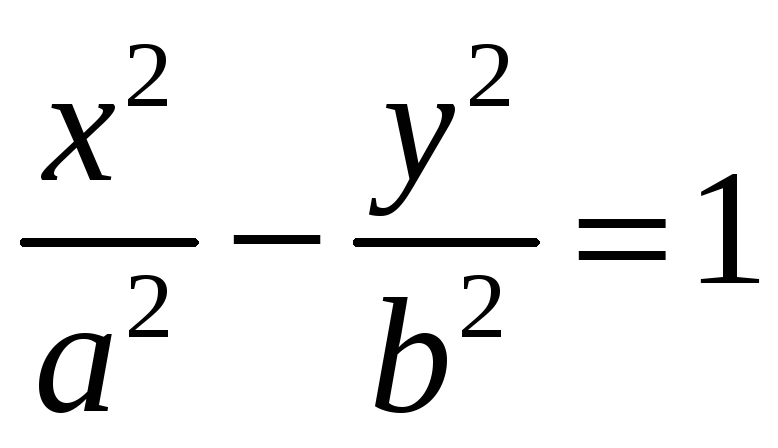
102. Задание {{1}} ТЗ1

Укажите каноническое уравнение параболы

R

103. Задание {{1}} ТЗ1

Уравнение окружности радиуса R=3 с центром в точке С (–12) имеет вид

R (x+1)²+(y-2)²=9

104. Задание {{1}} ТЗ1

Уравнение эллипса, у которого большая полуось а=5, а малая полуось b=3 имеет вид

R

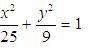
105. Задание {{1}} ТЗ1

Уравнение эллипса, у которого большая полуось а=6, а малая полуось b=2 имеет вид

R

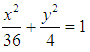
106. Задание {{1}} ТЗ1

Геометрическое место точек, разность расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная, называется

R гиперболой

107. Задание {{1}} ТЗ1

Геометрическое место точек, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная, называется

R эллипсом

108. Задание {{1}} ТЗ1

Геометрическое место точек, равноотстоящих от данной точки, называемой фокусом, и данной прямой, называемой директрисой, есть

R парабола

109. Задание {{1}} ТЗ1

Дано уравнение окружности: . Ее радиус R и координаты центра С равны

R R=4, C(1-3)

110. Задание {{1}} ТЗ1

Уравнение гиперболы, у которой действительная полуось а=4, а мнимая полуось b=3, имеет вид

R

Средний уровень

111. Задание {{1}} ТЗ1

Даны уравнения кривых:

1) : 2) : 3) : 4) .

Окружность описывают уравнения:

R 1,2

112. Задание {{1}} ТЗ1

Даны уравнения кривых:

1) 2) 3) 4) .

Эллипс описывают уравнения:

R 2,4

113. Задание {{1}} ТЗ1

Даны уравнения кривых:

1) 2) 3) 4) 5) .

Гиперболу описывают уравнения:

R 2,3

114. Задание {{1}} ТЗ1

Дано уравнение гиперболы .

Уравнения ее асимптот имеют вид:

R

115. Задание {{1}} ТЗ1

Дано уравнение гиперболы . Координаты ее вершин (А₁ и А₂) :

R А₁ (–40), А₂(40)

116. Задание {{1}} ТЗ1

Дана парабола . Координаты ее фокуса F и уравнение директрисы

R F (10), x = –1

117. Задание {{1}} ТЗ1

Уравнение окружности радиуса R=4 с центром в точке С(2 –3) имеет вид

R (x–2)²+(y+3)² = 16

118. Задание {{1}} ТЗ1

Уравнение параболы, у которой фокус имеет координаты F(0,2), а директриса имеет уравнение x = –2, имеет вид

R y ² = 8x

Высокий уровень

120. Задание {{1}} ТЗ1

Расстояние между фокусами эллипса равно 6, а малая полуось b=4. Тогда уравнение этого эллипса имеет вид

R

121. Задание {{1}} ТЗ1

Дано уравнение эллипса: . Координаты его фокусов:

R F₁(-40) F ₂(40)

122. Задание {{1}} ТЗ1

Дана гипербола: . Координаты ее фокусов

R F ₁(-50) F ₂(50)

123. Задание {{1}} ТЗ1

Дано уравнение окружности: . Уравнение прямой, проходящей через ее центр параллельно прямой имеет вид

R

Б-базовый (11)

С-средний (8)

Т-Высокий (4)

Тема 7. Прямая и плоскость в пространстве

Базовый уровень

124. Задание {{1}} ТЗ1

Канонические уравнения прямой линии в пространстве переменных x,y,z имеют вид:

R

125. Задание {{1}} ТЗ1

Уравнение плоскости имеет вид: x–2y+5z–4=0. Вектор , перпендикулярный этой плоскости имеет координаты

R {1, –2,5}

126. Задание {{1}} ТЗ1

Направляющий вектор прямой линии, заданной каноническими уравнениями , имеет координаты

R

127. Задание {{1}} ТЗ1

Дано уравнение плоскости:.

Вектор , перпендикулярный этой плоскости имеет координаты

R {1,2,–5}

Средний уровень

128. Задание {{1}} ТЗ1

Параметрические уравнения прямой линии в пространстве переменных x,y ,z имеют вид:

R

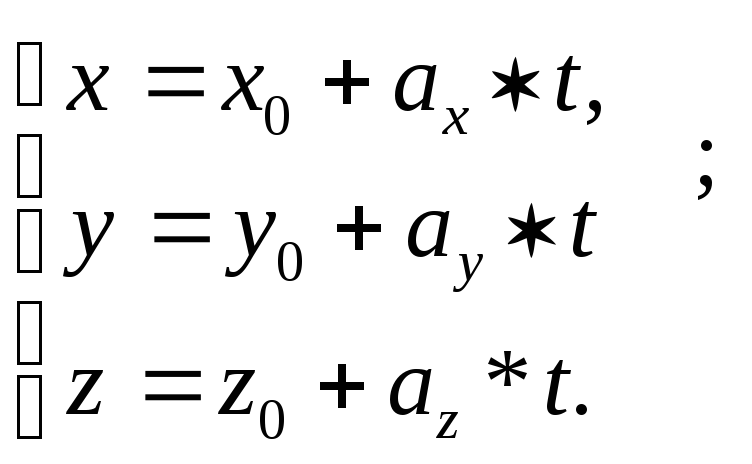
129. Задание {{1}} ТЗ1

Укажите уравнение плоскости, проходящей через данную точку перпендикулярно вектору .

R

R .

130. Задание {{1}} ТЗ1

Расстояние от точки до плоскости , заданной уравнением , вычисляют по формуле

R

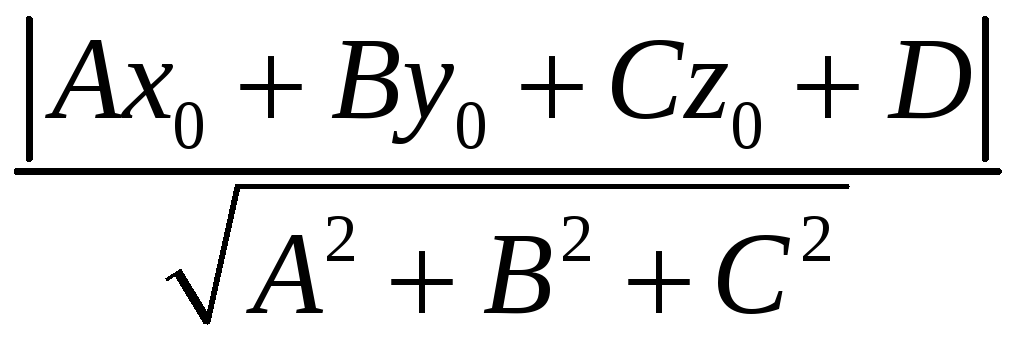
Высокий уровень

131. Задание {{1}} ТЗ1

Каноническим уравнением прямой 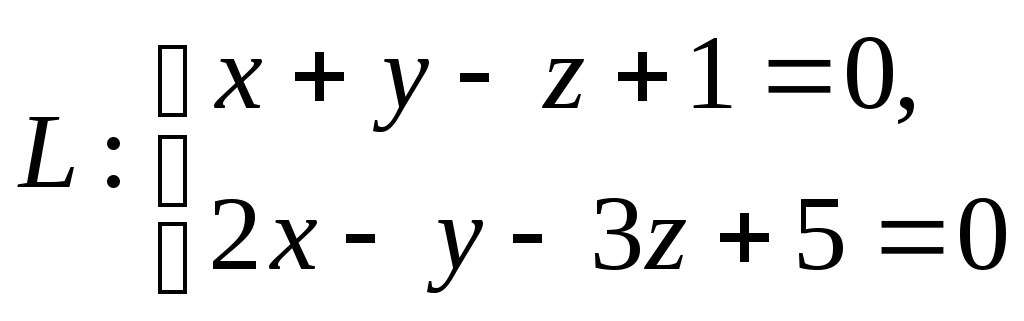является уравнение

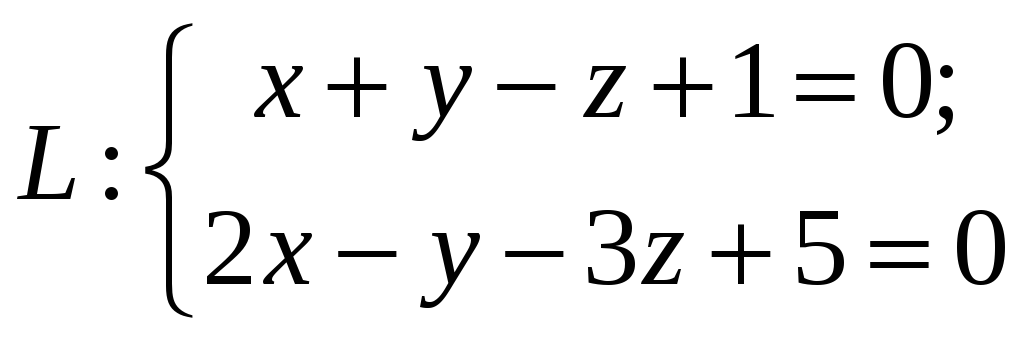
R

132. Задание {{1}} ТЗ1

Уравнение плоскости, проходящей через точку М(1,2,0) перпендикулярно вектору ,имеет вид

R

133. Задание {{1}} ТЗ1

Даны две прямые: и . Косинус угла между ними равен

R

Б-базовый (4)

С-средний (3)

Т-Высокий (3)