Матрицы

Базовый уровень

1. Задание {{1}} тз1

Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется

R диагональной

2. Задание {{1}} ТЗ1

Матрица называется обратной матрице , если выполнятся условие

R

3.Задание {{1}} ТЗ1

Квадратную матрицу второго порядка принято обозначать символом

R

4. Задание {{1}} ТЗ1

Квадратная матрица называется треугольной, если

R все элементы, расположенные по одну сторону от главной диагонали, равны нулю

5. Задание {{1}} ТЗ1

Единичную матрицу второго порядка принято обозначать символом

R

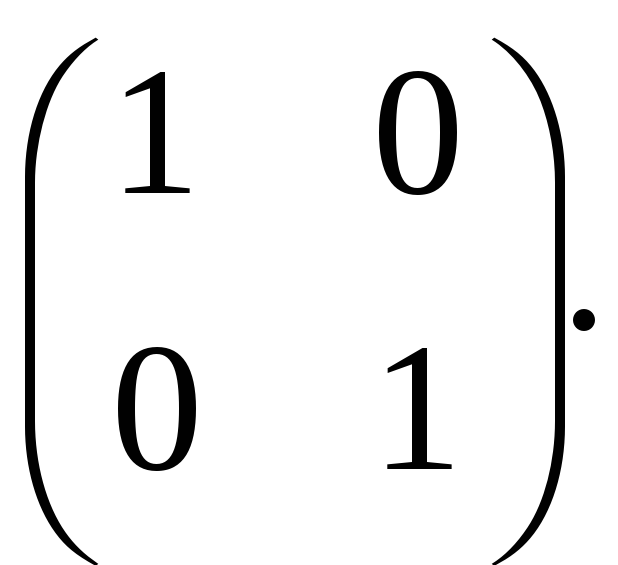
6. Задание {{1}} ТЗ1

Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется

R транспонированной

7. Задание {{1}} ТЗ1

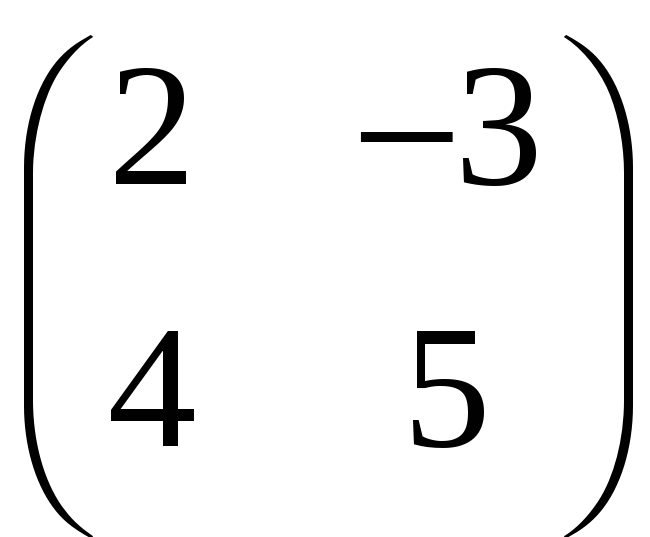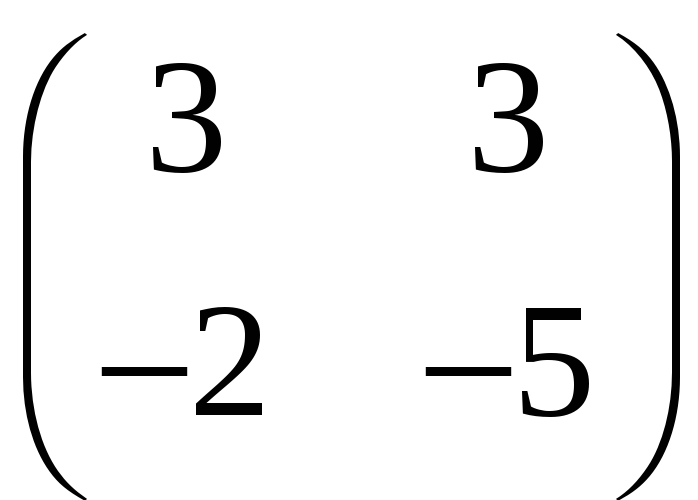Сумма матриц и равна

R

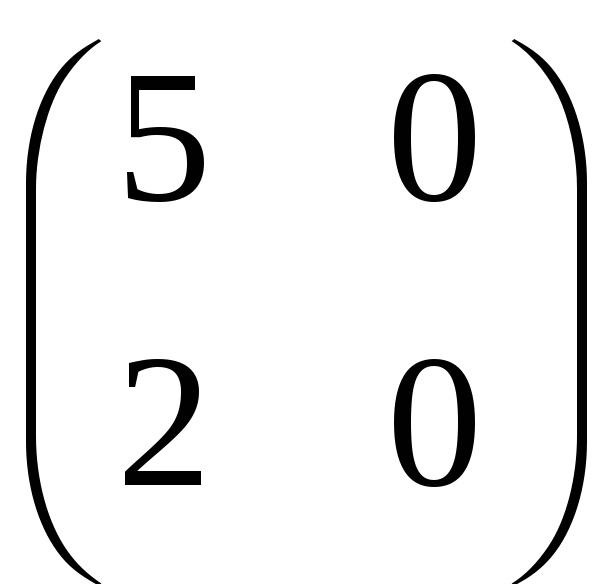
8. Задание {{1}} ТЗ1

Сумма элементов главной диагонали матрицы равна

R 7

9.Задание {{1}} ТЗ1

Сумма элементова+а+а матрицы А=равна

R 2

10. Задание {{1}} ТЗ1

Сумма элементов главной диагонали матрицы равна

R –7

Средний уровень

11. Задание {{1}} ТЗ1

Суммой двух матриц и называется матрица , (,) такая, что:

R

12. Задание {{1}} ТЗ1

Разностью двух матриц и называется матрица , (,) такая, что:

R

13. Задание {{1}} ТЗ1

Произведением матрицы на матрицу называется матрица , такая, что:

R

14. Задание {{1}} ТЗ1

Матрица, обратная данной 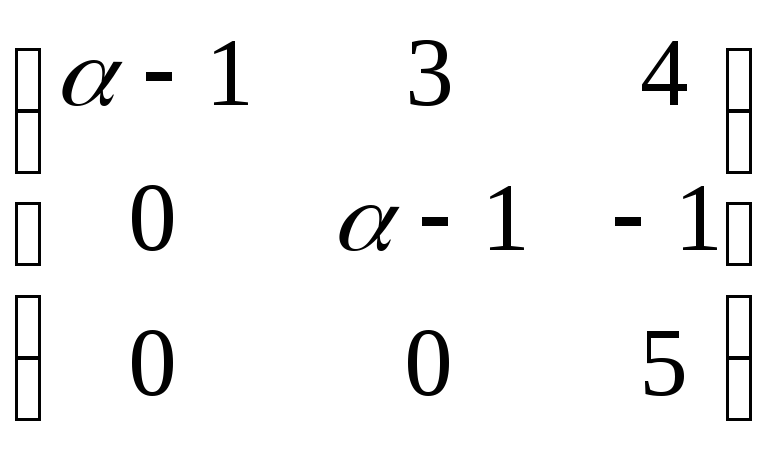, не существует при , равном

R 1

15. Задание {{1}} ТЗ1

Матрица, обратная данной 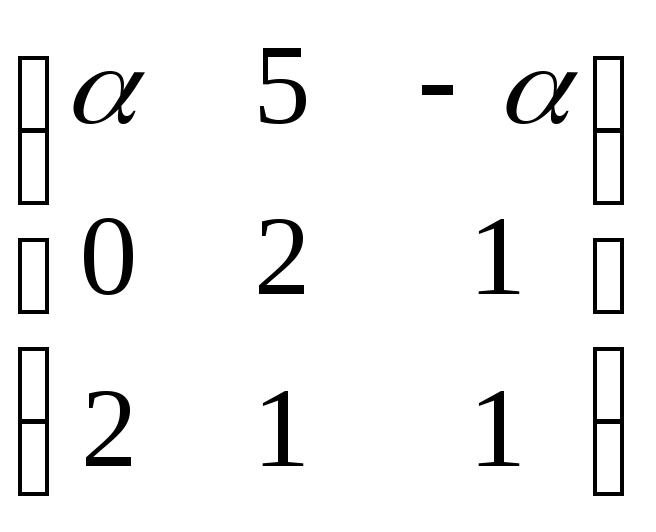, не существует при , равном

R -2

Высокий уровень

16. Задание {{1}} ТЗ1

Ранг матрицы равен:

R 2

17. Задание {{1}} ТЗ1

Ранг матрицы равен:

R 2

18. Задание {{1}} ТЗ1

Ранг матрицы 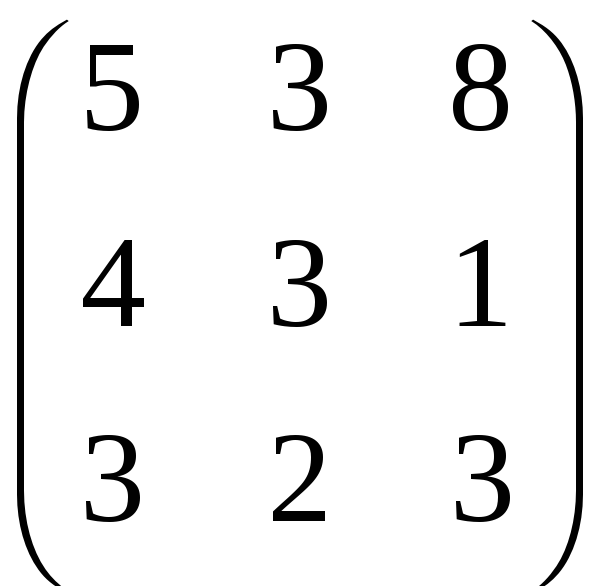равен:

R 2

19. Задание {{1}} ТЗ1

Матрица, обратная данной А=, имеет вид

R

20. Задание {{1}} ТЗ1

Матрица, обратная данной В=, имеет вид (равна)

R

Б - базовый (11)

С - средний (5)

Т - Высокий (5)

Определители

Базовый уровень

21. Задание {{1}} ТЗ1

Определитель второго порядка – это число, которое принято обозначать символом:

R

22. Задание {{1}} ТЗ1

Определитель второго порядка – это число, которое вычисляют по формуле:

R

23. Задание {{1}} ТЗ1

Определитель третьего порядка – это число, которое принято обозначать символом:

R *

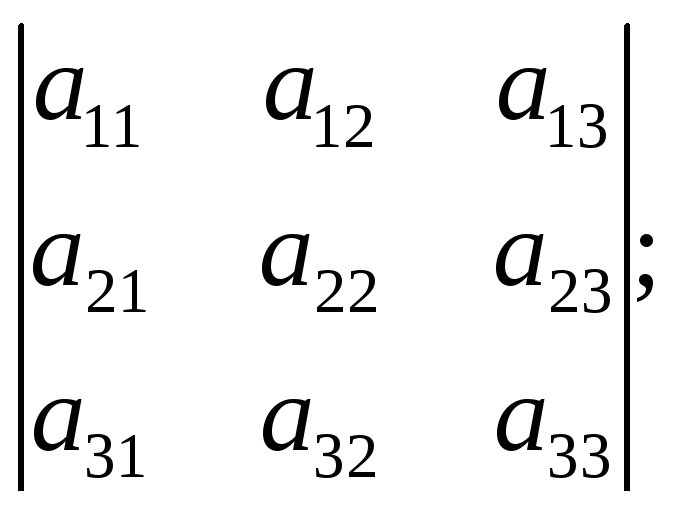
Средний уровень

24. Задание {{1}} ТЗ1

Если вычеркнуть из определителя D порядка n строку с номером 3 и столбец с номером 3, то получится определитель порядка n-1, который называют:

R минором элемента a₃₃ определителя D и обозначают символом M₃₃

25. Задание {{1}} ТЗ1

Алгебраическое дополнение элемента a₁₃ определителя

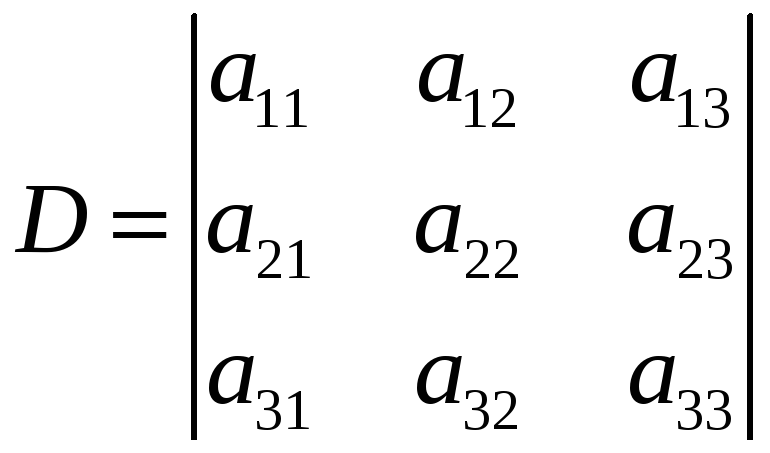
R обозначают A₁₃ и вычисляют по формуле

26. Задание {{1}} ТЗ1

Разложение определителя по элементам второго столбца имеет вид:

R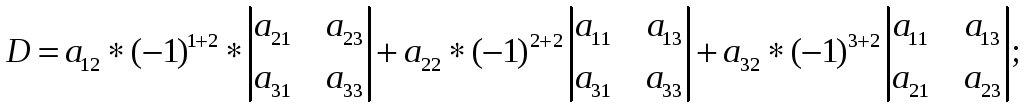

27. Задание {{1}} ТЗ1

Разложение определителя по элементам второго столбца имеет вид:

R

28. Задание {{1}} ТЗ1

Определитель третьего порядка – это число, которое вычисляют по формуле:

R

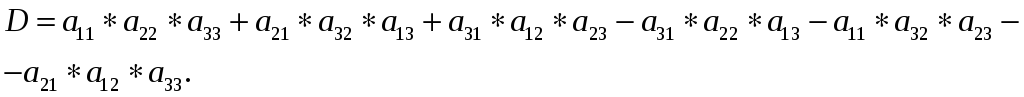
29. Задание {{1}} ТЗ1

Разложение определителя 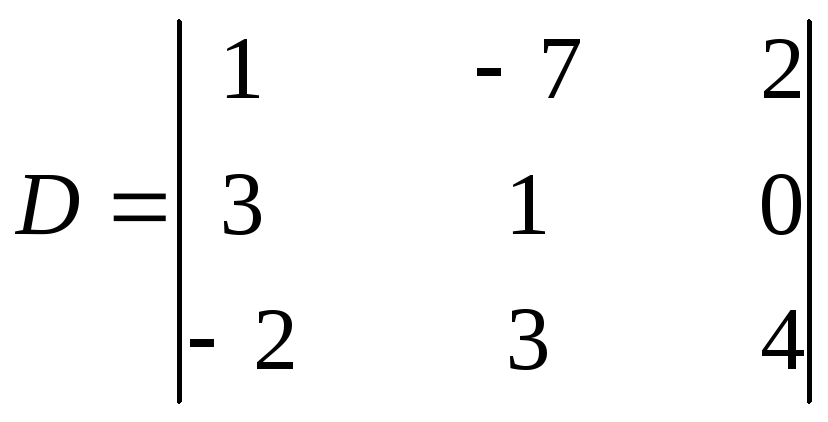по элементам второй строки имеет вид:

R

30. Задание {{1}} ТЗ1

Алгебраическое дополнение элемента определителя

R обозначают A_ij и вычисляют по формуле

31. Задание {{1}} ТЗ1

Разложение определителя 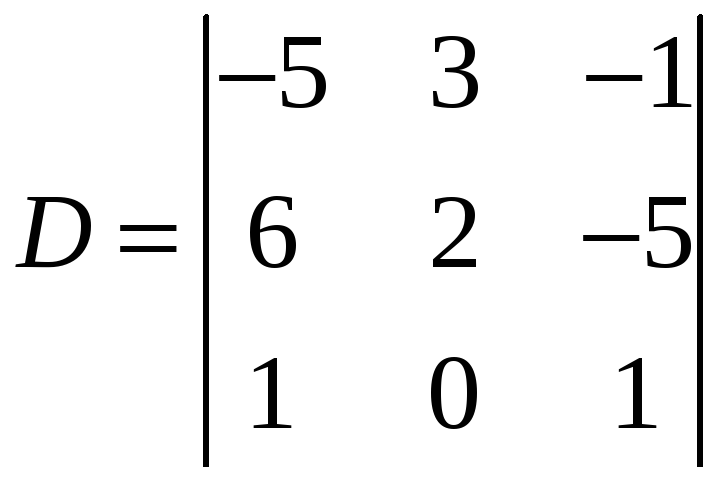по элементам второго столбца имеет вид:

R

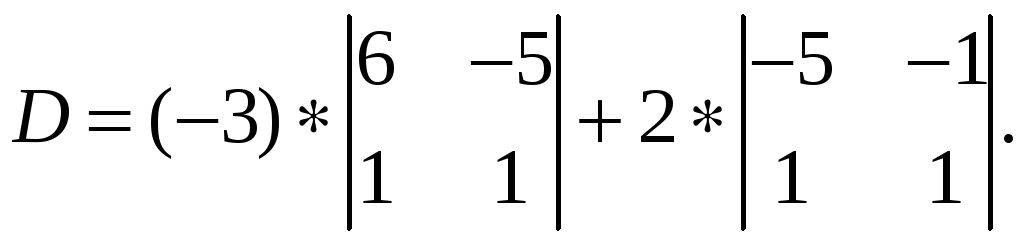
Высокий уровень

32. Задание {{1}} ТЗ1

Определитель 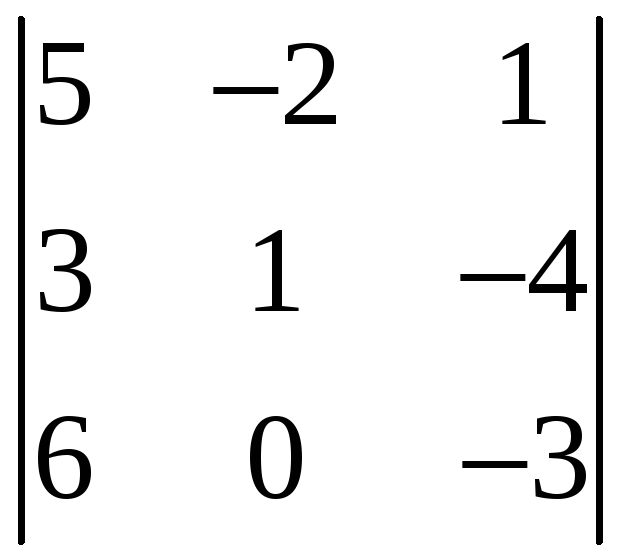равен:

R 9

33. Задание {{1}} ТЗ1

Определитель 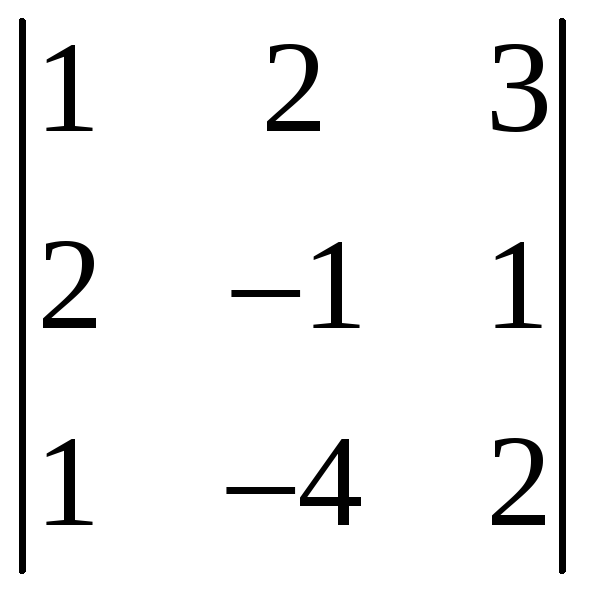равен:

R -25

34. Задание {{1}} ТЗ1

Определитель 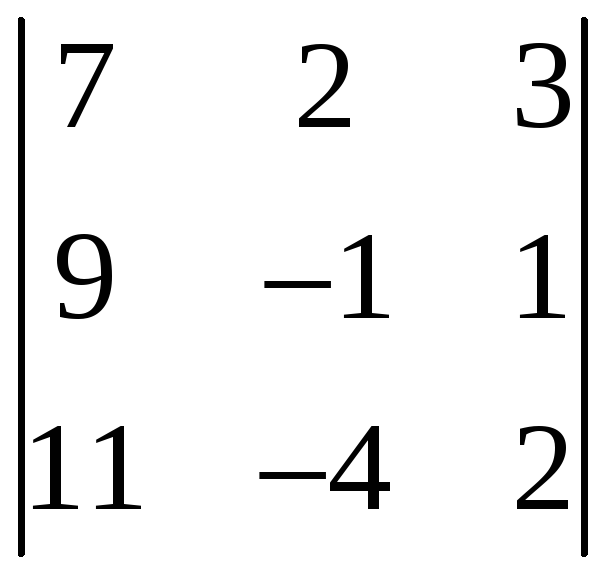равен:

R -75

Б – базовый(3)

С – средний(8)

Т – Высокий(3)