
- •ВВЕДЕНИЕ
- •1. ХИМИЧЕСКАЯ КИНЕТИКА
- •1.1. Основные понятия и определения
- •1.2. Основной постулат химической кинетики
- •1.3. Формальная кинетика
- •1.4. Некоторые методы определения порядка реакции
- •1.5. Влияние температуры на скорость химической реакции
- •1.6. Методы расчета энергии активации
- •2. КАТАЛИЗ
- •2.1. Основные понятия и определения
- •2.2. Теория промежуточных соединений в катализе
- •2.3. Термодинамические и кинетические аспекты каталитических процессов
- •2.4. Гомогенный катализ. Простейшие механизмы гомогенных каталитических реакций
- •2.5. Гетерогенный катализ
- •3. ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
- •5. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- •ЛИТЕРАТУРА
- •ОГЛАВЛЕНИЕ
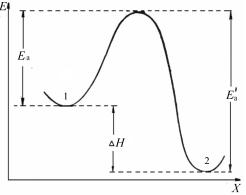
система переходит на более низкий энергетический уровень. Изменение потенциальной энергии системы вдоль пути реакции (или вдоль координаты реакции х) представляют в виде энергетической диаграммы.
На рис. 7 изображена энергетическая диаграмма элементарной экзотермической реакции А +ВС [АВС]= → АВ +С. Кривая показывает, как изменяется потенциальная энергия системы в процессе реакции. Эта кривая энергетически описывает весь путь реакции, т. е. совокупность наиболее вероятных состояний системы. На вершине энергетического барьера система находится в переходном состоянии или в состоянии активированного комплекса, а высота барьера определяет энергию активации Eа прямой реакции.
Рис. 7. Изменение потенциальной энергии системы при протекании элементарной химической реакции (x — координата реакции; H — изменение энтальпии)
В соответствии с уравнением Аррениуса, чем меньше энергия активации, тем больше константа скорости реакции и тем больше скорость химической реакции.
1.6. Методы расчета энергии активации
Рассмотрим методы расчета энергии активации. Для расчета
энергии активации используют уравнение Аррениуса.
1. Графический метод. Запишем уравнение Аррениуса (см. (41)) в логарифмической форме:
22
lnk = lnZ −Eа/(RT), |
(43) |
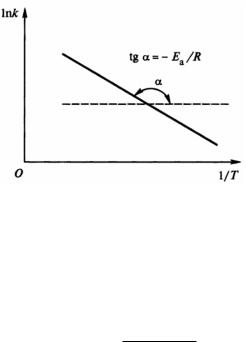
удобной для графического определения энергии активации. Энергию активации можно найти по значениям константы скорости реакции, измеренным при нескольких значениях температуры. При этом экспериментальные данные представляют в координатах Аррениуса (lnk; 1/T). Тангенс угла наклона полученной прямой линии равен (−Eа/R) (рис. 8).
Рис. 8. Графическое определение энергии активации
2. Аналитический метод. Уравнение Аррениуса (см. (41)) можно представить в дифференциальной форме:
dlnk |
= |
Ea |
. |
(44) |
dT |
|
|||
|
RT2 |
|
||
Тогда, интегрируя уравнение (44) в пределах от T1 до T2, получаем
ln(k2/k1) = |
Ea(T2 −T1) |
. |
(45) |
||
|
|
RT2T1 |
|
||
Из уравнения (45) следует: |
|
|
|
|
|
Ea = |
RT1T2 ln(k2/k1) |
. |
(46) |
||
|
|||||
|
T2 −T1 |
|
|||
Таким образом, энергию активации можно рассчитать аналитически по формуле (46), если известны константы скорости реакции при двух значениях температуры T1 и T2. Однако такой
23
