Федеральное агентство по образованию

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ МАШИНОСТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ

Кафедра «Прикладная математика »

ОТЧЕТ

ПО ПРЕДДИПЛОМНОЙ ПРАКТИКЕ НА ТЕМУ:

«Исследование решений нечеткой модели Лефевра-Николиса»

Выполнил: студент группы К-44

Баталин М. С.

Проверил: д.ф.-м.н., проф.

Бутусов О.Б.

Оценка при защите отчета_____

2015 г.

Содержание

Введение.

Глава 1. Двухмерная дифференциальная нечеткая математическая модель Лефевра-Николиса.

1.1. Нечеткая и интервальная формулировка модели.

1.2. Элементы теории нечетких множеств.

Глава 2. Математическая и компьютерная модель Лефевра-Николиса с нечеткими параметрами.

2.1. Разработка математической модели.

2.2. Разработка архитектуры компьютерной модели и пользовательского интерфейса для управления моделью.

3. Заключение.

Введение.

Надорганизменные системы, которые изучает экология – популяции, биоценозы, экосистемы, – чрезвычайно сложны. В них возникает множество взаимосвязей, сила и постоянство которых непрерывно меняются. Одни и те же внешние воздействия могут привести к различным, иногда прямо противоположным результатам, в зависимости от того, в каком состоянии находилась система в момент воздействия.

Предвидеть ответные реакции системы на действие конкретных факторов можно лишь через сложный анализ существующих в ней количественных взаимоотношений и закономерностей. В экологии поэтому широкое распространение получил метод математического моделирования как средство изучения и прогнозирования природных процессов.

Суть метода заключается в том, что с помощью математических символов строится абстрактное упрощенное подобие изучаемой системы. Затем, меняя значение отдельных параметров, исследуют, как поведет себя данная искусственная система, т. е. как изменится конечный результат.

Модели строят на основании сведений, накопленных в полевых наблюдениях и экспериментах. Чтобы построить математическую модель, которая была бы адекватной, т. е. правильно отражала реальные процессы, требуются существенные эмпирические знания. Отразить все бесконечное множество связей популяции или биоценоза в единой математической схеме нереально. Однако, руководствуясь пониманием, что в надорганизменных системах имеется внутренняя структура и, следовательно, действует принцип “не все связи существенны”, можно выделить главные связи и получить более или менее верное приближение к действительности.

В построении математических моделей сложных процессов выделяются следующие этапы.

1. Прежде всего, те реальные явления, которые хотят смоделировать, должны быть тщательно изучены: выявлены главные компоненты и установлены законы, определяющие характер взаимодействия между ними. Если неясно, как связаны между собой реальные объекты, построение адекватной модели невозможно. На этом этапе должны быть сформулированы те вопросы, ответ на которые должна дать модель. Прежде чем строить математическую модель природного явления, надо иметь гипотезу о его течении.

2. Разрабатывается математическая теория, описывающая изучаемые процессы с необходимой детальностью. На ее основе строится модель в виде системы абстрактных взаимодействий. Установленные законы должны быть облечены в точную математическую форму. Конкретные модели могут быть представлены в аналитической форме (системой аналитических уравнений) или в виде логической схемы машинной программы. Модель природного явления есть строгое математическое выражение сформулированной гипотезы.

3. Проверка модели – расчет на основе модели и сличение результатов с действительностью. При этом проверяется правильность сформулированной гипотезы. При значительном расхождении сведений модель отвергают или совершенствуют. При согласованности результатов модели используют для прогноза, вводя в них различные исходные параметры.

Следует, однако, отметить, что сама по себе математическая модель не может служить абсолютным доказательством правильности той или иной гипотезы, так как может оказаться, что разные гипотезы приводят к сходным результатам, но она служит одним из путей анализа реальности.

Основные успехи и достижения современной математической экологии связаны главным образом с бурным развитием компьютерной техникики и компьютерной математики, разработкой теории детерминированного хаоса и широким применением в математической экологии методов качественной теории дифференциальных уравнений.

Теория детерминированного хаоса, которую ввел в науку метеоролог Эдвард Лоренц в 1960 году, привела к революционному изменению научных представлений и взглядов на теорию движения и эволюции широкогокруга физических, химичсеких, биологических, экономических и социальных систем. В теории хаоса инструментом изучения динамики сложных объектов являются системы нелинейных дифференциальных уравнений, получившие название дифференциальных моделей. Динамика большинсвта систем, описываемых более чем тремя обыкновенными дифференциальными уравнениями первого порядка, оказывается в высшей степени непредсказуемой.

Хаотичсекое поведение проявляется не только в дифференциальных моделях, но и в простейших дискретных отображениях. Классическое одномерное и одношаговове дискретное отображение, названное дискретной логистической моделью, широко известно в математической экологии и служит для моделирования динамики и эволюции биологических популяций.

Важным результатом развития методов математического моделирования сложных систем явилось открытие так называемых базовых математических моделей. Эти базовые математические модели являются общими для разнообразных систем и явлений.

Экологическая модель, в которой учитывается взаимодействие нескольких биологических видов, базовая экологическая модель Лефевра-Николиса. Эта двухмерная экологическая модель рассмотрена в дипломной работе посредством моделирования ее в среде Matlab. Фазовый портрет модели можно исследовать с помощью симулинк-модели, для управления которой служит Матлаб-программа. Исследование происходит при некоторых изменениях заданных параметров, тем самым изменяя режим затухающих колебаний в режим автоколебаний.

Глава 1. Двухмерная дифференциальная нечеткая математическая модель Лефевра-Николиса.

В ряде физических, химических, биологических и других систем могут возникать незатухающие колебания, амплитуда и период которых не зависят от начальных условий. Во всяком случае, изменение начальных условий вшироких пределах не оказывает влияния на характер колебаний. На фазовой плоскости автоколебаниям соответствуют предельный цикл — замкнутая траектория, на которую наматываются все фазовые траектории из некоторой окрестности. Таким образом, предельный цикл является аттрактором. Однако, в отличие, например, от фокуса, это не изолированная особая точка, а изолированная особая траектория. Различают устойчивые предельные циклы, когда все фазовые траектории из некоторой трубчатой окрестности стремятся к нему при t стремящемся к бесконечности, т.е. фазовые траектории наматываются на предельный цикл с двух сторон; неустойчивые предельные циклы, когда все фазовые траектории стремятся к предельному циклу при t стремящемся к минус бесконечности, т.е. фазовые траектории сматываются с предельного цикла полуустойчивые, когда с одной стороны фазовые траектории наматываются на предельный цикл (стремятся к нему при t стремящемся к плюс бесконечности), а с другой стороны сматываются (стремятся к предельному циклу при t стремящемся к минус бесконечности).

Автоколебания — незатухающие колебания в диссипативных нелинейных системах, которые поддерживаются за счет внешнего источника энергии. Вид и свойства этих колебаний (частота, амплитуда, форма) определяются самой системой и не зависят от начальных условий. Характерная особенность автоколебаний — отсутствие внешнего периодического воздействия. Схематично автоколебательную систему можно представить в виде источника энергии, осциллятора с затуханием и обратной связи (нелинейного элемента).

Осциллятор сам регулирует поступление энергии от внешнего источника, что отличает автоколебания от вынужденных колебаний, когда внешний источник определяет, когда и сколько энергии передать осциллятору, задавая тем самым частоту, амплитуду, фазу и форму колебаний. При автоколебаниях, благодаря наличию нелинейного элемента обеспечивается согласование подачи энергии с работой осциллятора. Автоколебания окружают нас повсюду в природе и технике: часы, звучащая скрипичная струна или органная труба, бьющееся сердце — все эти системы совершают автоколебания.

Рождение предельного цикла происходит при возбуждении в системе автоколебаний. Подобное явление наблюдается при изменении параметров колебательной системы. Исходный режим затухающих колебаний при достижении колебаний системными параметрами пороговых значений переходит в режим автоколебаний. На фазовом портрете это соответствует тому, что устойчивая особая точка при некоторых значениях параметров теряет устойчивость, и образуется устойчивый предельный цикл, который выполняет функции аттрактора. Подобная перестройка фазовых портретов получила название бифуркации Хопфа. Бифуркация-изменение характера движения динамической системы на большом временном интервале при изменении одного или нескольких параметров. Те значения параметров, при которых изменяются качественные или топологические свойства движения, называются критическими или бифуркационными значениями.

В 1971 г. Лефевр и Николис предложили модель, описывающую колебательные процессы в химической реакции. Они рассмотрели цепочку химических превращений, используя экологическую интерпретацию:

В этой экологической системе биологический вид Χ погибает при встрече с видом B, и становится при этом пищей для вида Υ. Прямое же взаимодействие видов Χ и Υ приводит к гибели вида Υ и увеличению численности вида Χ. Дифференциальная модель этой экологической системы имеет вид:

Эта модель является классическим примером системы, в которой происходит бифуркация Хопфа. Нечеткая двухмерная дифференциальная модель отображает переход от устойчивого фокуса к предельному циклу путем попадания параметра b в границы интервала b1 и b2. Остальные параметры системы являются фиксированными. Теория неопределенности нечетких или интервальных параметров системы показывает степень принадлежности интервального числа, используется функция принадлежности. Функция принадлежности равна единице в любой из точек интервала. Нечеткие числа с произвольной функцией принадлежности отличаются от интервальных чисел тем, что при вычислениях с нечеткими числами требуется выполнять преобразования функции принадлежности, необходимые для представления результата в виде нечеткого числа, т.е. в виде интервала и результирующей функцией принадлежности. Одним из методов вычислений с нечеткими числами является представление исходных функций принадлежности в виде множества интервалов, полученных с помощью α-сечений. Для каждого из полученных интервалов вычисляется интервал результата, на концах которого значения функции принадлежности равны уровню α-сечения. В результате функция принадлежности находится методом объединения результатов, полученных по отдельным точкам. Основные формулы интервальной арифметики:

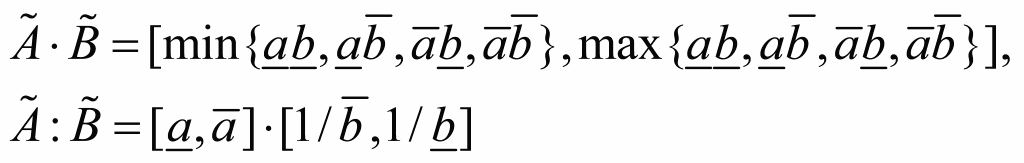
Используется обычный метод Эйлера для решения нечеткого дифференциального уравнения.