Тронин В.Н. - Заметки об эволюции (1988)

Поскольку математически уравнения ,описывающие образование оргпреступности совпадают с уравнениями применяемыми при описании фазовых переходов первого рода, то в рамках рассматриваемой модели, процесс формирования оргпреступности выглядит следующим образом:

организованной преступности происходит локально за счет флуктуаций (образование территориальных преступных группировок). Если размер территории, контролируемой данной группировкой, достаточно велик, то такая группировка распространяет свое влияние на все большие и большие территории.

Проведенное рассмотрение относится только к начальной стадии формирования оргпреступности. По мере роста числа группировок среднее число банкиров, за счет которых "живут" группировки, уменьшается (см.(35)):

n1=n1(0)-Sξ2;

Г

S= β ;

Флуктуационное возникновение новых устойчивых группировок на этой стадии практически исключено, поскольку критический размер ρ с весьма велик. Увеличение критического размера, сопровождающее прогрессирующее падение числа банкиров, приводит к тому, что группировки, контролирующие небольшие территории становятся подкритическими (ρ<ρ с) и исчезают. Таким образом, на этой стадии определяющую роль приобретает процесс поедания мелких группировок более крупными - рост крупных группировок происходит за счет исчезновения мелких. Такой процесс носит название коалесценции. Описание динамики этого процесса подробно изложено в [5] .Качественные результаты этого рассмотрения таковы:

Рассмотренный пример демонстрирует самосогласованный (эволюционный) подход к образованию в сложной системе коллективной моды. Действительно, в результате развития описанных выше процессов, рассматриваемая система стремится к самосогласованному состоянию, которое определяет как число выживших банкиров, так и число выживших преступников. Существуют, однако, примеры систем, поведение которых носит неэволюционный (в описанном выше смысле) характер. К описанию примера поведения такой системы мы сейчас перейдем.

Поляризация общественного мнения. Фазовый переход 1го рода, индуцированный внешним полем.

Рассмотрим модель формирования общественного мнения в случае h≠0 . Соответствующее уравнение, определяющее разницу между числом индивидуумов, имеющих мнение "за" и "против" ψ = n+ − n− , имеет вид:

Предположим, что показатель общественного климата Т достаточно мал так, что а>0 (недемократическое общество). Низкий показатель общественного климата указывает на способность общества к переменам. Стационарные решения уравнения (14) находятся из условия

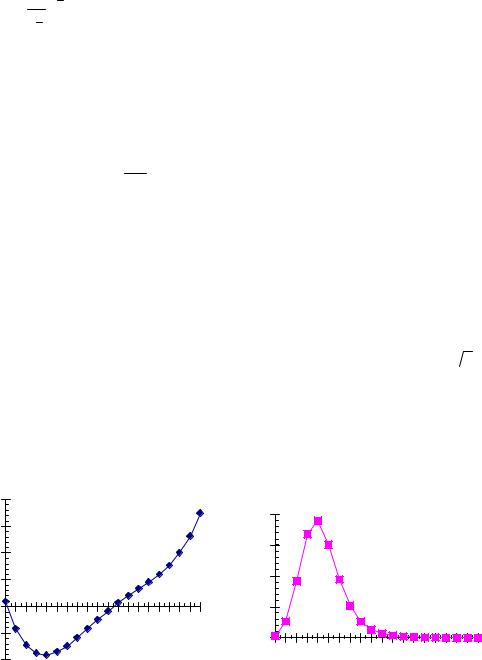
При а>0 левая сторона уравнения (15) немонотонная функция, в результате чего в определенном интервале значений h уравнение имеет три различных вещественных корня, так, что функция ψ (h)

В.Н. ТРОНИН 51 ЗАМЕТКИ ОБ ЗВОЛЮЦИИ

Глава 2.Жизнь.

становится немонотонной .Границы этого интервала определяются, очевидно, из условия

и даются неравенствами -ht<h<ht,где

2 3

ht= 3 a 2

32

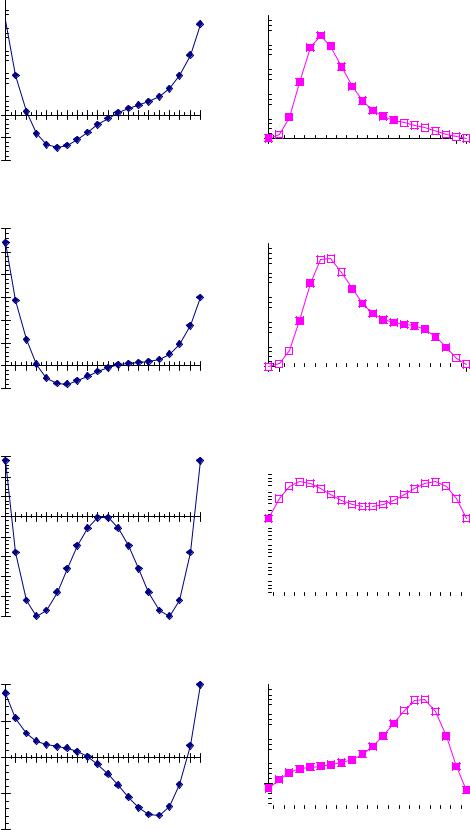
Легко видеть, что ситуация, изображенная на рисунке 4 с),d),e),f),i),k), отвечает неустойчивым состояниям: потенциал, отвечающий уравнению (14)

минимален, но величина этого минимума превышает величину другого минимума. Другими словами, этой ситуации отвечают метастабильные состояния системы. Таким образом, если при заданном a<0 менять внешнее поле h ,то при прохождении параметром h значения h=0,возникает фазовый переход первого рода. В этой точке находятся в равновесии друг с другом "фазы" с противоположным по знаку значением параметра ψ = ± а . Вид потенциала, отвечающий рассмотренному случаю при различных значениях внешнего поля h показан на рисунке 4.

Глава 2.Жизнь.

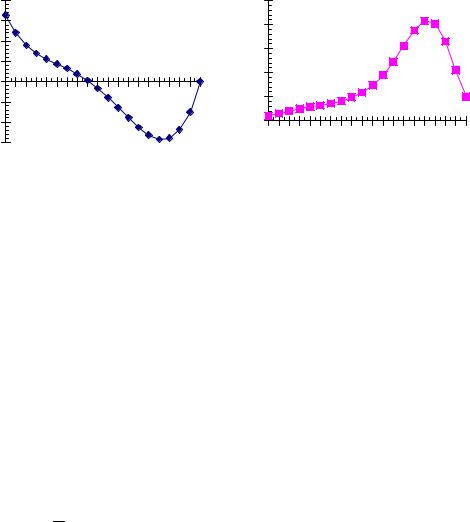
Рис 4 Зависимость потенциала и функции распределения в модели формирования общественного мнения при различных значениях параметра h-a) h= -0.9,b) h= -0.6;c) h= -0.3

Наличие фазового перехода первого рода в изучаемой системе позволяет сделать вывод о том, что фазовый переход протекает путем образования зародышей новой фазы - локализованных участков территории, на которой мнение, например, "за" преобладает над мнением "против ", в то время как на всей остальной территории мнение "против" преобладает над мнением «за».

Анализ, аналогичный проделанному в предыдущем разделе, показывает, что уравнение роста такого зародыша определяется соотношением (в безразмерных единицах):

Существенным отличием рассмотренного в настоящем разделе фазового перехода состоит в отсутствии режима коалесценции. Внешнее поле h не зависит самосогласованным образом от характеристик системы. Именно это обстоятельство и определяет неэволюционный характер рассмотренного фазового перехода - система не "подстраивается" под изменение размеров возникающих зародышей. Исчезновение внешнего поля приводит к полному растворению возникших зародышей.

Применим рассмотренную модель к анализу формирования общественного мнения в случае проведения в России кампании по выборам Президента в 1996 году. Будем считать, что имеется всего два кандидата - Б. Н. Ельцин и Г. А. Зюганов. Выбор мнения за

Глава 2.Жизнь.

Ельцина автоматически означает выбор против Зюганова и наоборот. К 1996 году в обществе имелось как минимум два существенных фактора:

1.Политика, проводимая за первый срок президентства Ельцина, привела к формированию в обществе тенденции к необходимости перемен (низкий показатель общественного климата Т).

2.Ностальгические настроения значительной части общества, и разумная политика коммунистов привели к формированию внешнего информационного поля h0,способствовавшего победе Зюганова.

В рассмотренной ситуации, очевидно, что a>0,а рейтинги кандидатов n+ ,n− определяются соотношениями

отрицательный корни уравнения (15) при h = h0 > 0. Очевидно, что рейтинг Зюганова значительно превышает рейтинг Ельцина - ситуация, имевшая место в начале 1996 года. В это время действующий Президент России - Б. Н. Ельцин начал проводить интенсивную предвыборную кампанию с использование всех доступных ему средств массовой информации - телевидения, радио, газет, журналов и.т.д. Это привело к возникновению в системе дополнительного внешнего поля h1 < 0 . Таким образом, полное

результате полное внешнее поле стало отрицательным. В системе произошел фазовый переход первого рода, причем по сценарию образования зародышей новой "фазы" - значительного числа регионов, проголосовавших за Б. Н. Ельцина. Отметим, однако, что такая система неустойчива - отсутствие внешней агитации через средства масс-медиа (выключение поля h1 ) без изменения внутренней политики (прежде всего экономической) (поле h0 ) и, как следствие, общественного климата, возвращает общество в исходное состояние, когда коммунисты в значительной степени определяют общественное мнение. Равнодушие значительного числа избирателей, например молодежи (малые n0), лишь способствуют этому процессу.

Рассмотренная модель, естественно, является приближенной, так как не учитывает, например, многообразие кандидатов в

Глава 2.Жизнь.

Президенты, образование между ними коалиций и.т.д., однако даже она качественно отражает некоторые черты реальных процессов.

В заключение данного раздела коротко остановимся на анализе модели, описывающей лазер, динамику популяции или торговую точку. Соответствующее уравнение (уравнение Ферхюльста) имеет вид

Решение (18) с начальным условием n(t = 0)= n (0) имеет вид:

График зависимости n(t) приведен на рисунке 5.

X

2,0

1,5

1,0

Рис 5. Зависимость от времени количества товара, проданного торговой точкой в модели торговца.

статистического анализа, заметим, что рассматриваемая система потенциальна

Глава 2.Жизнь.

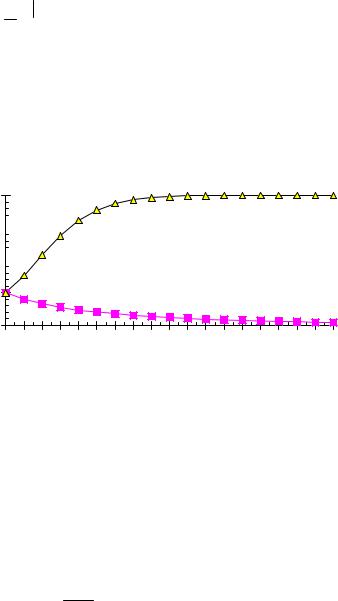
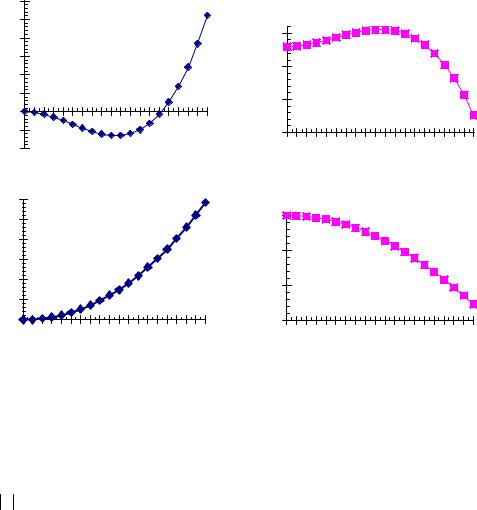
На рисунке 6 приведена зависимость потенциала и функции распределения f (n) ~ exp(− β V (n)) при различных значениях параметра

λ .

Рис 6. Зависимость потенциала и функции распределения в модели Ферхюльста.

Очевидно, что при λ > 0система с подавляющей вероятностью находится в состоянии с n = 0 .При λ ,< 0 основное состояние системы соответствует наличию ненулевого числа "особей "в "популяции" n = λ .Переход из одного состояния в другое происходит вследствие флуктуаций.

«непотенциальных» моделей. «Жесткие» и «мягкие» математические модели•

МОДЕЛЬ ВОЙНЫ ИЛИ СРАЖЕНИЯ.

В простейшей модели борьбы двух противников (скажем, двух армий) — модели Ланкастера — состояние системы описывается точкой { х , у) положительного квадранта плоскости. Координаты этой точки, х и у— это численности противостоящих армий. Основные уравнения модели имеют вид

x! = − by y! = − ax

Здесь а — мощность оружия армии ж, a b— армии у. Попросту говоря, предполагается, что каждый солдат армии х убивает за единицу времени а солдат армии у (и, соответственно, каждый солдат армии у убивает b солдат армии х). Точка над буквой здесь и далее означает производную по времени t. Это — жёсткая модель, которая допускает точное решение

dx by

dy = ax , axdx= bydy, ax2− by=2 const.

Эволюция численностей армий х и у происходит вдоль гиперболы, заданной этим уравнением (рис.А). По какой именно гиперболе пойдет война, зависит от начальной точки.

Эти гиперболы разделены прямой ax = by . Если начальная точка лежит выше этой прямой (случай 1 на рис. А), то гипербола выходит на ось у. Это значит, что в ходе войны численность армии х уменьшается до нуля (за конечное время). Армия у выигрывает, противник уничтожен.

Если начальная точка лежит ниже (случай 2), то выигрывает армия х. В разделяющем эти случаи состоянии (на прямой) война заканчивается ко всеобщему удовлетворению истреблением обеих армий. Но на это требуется бесконечно-большое время: конфликт продолжает тлеть, когда оба противника уже обессилены.

• Материал этого раздела взят из доклада В.И.Арнольда ««Жесткие» и «мягкие» математические модели» .Этот доклад был прочитан В.И.Арнольдом на Научнопрактическом семинаре «Аналитика в государственных учреждениях» в 1997 году.

Глава 2.Жизнь.

Рис. А. Жёсткая модель войны.

Рис. В. Мягкая модель войны.

Основной вывод из рассмотренной модели таков: для борьбы с вдвое более многочисленным противником нужно в четыре раза более мощное оружие, с втрое более многочисленным — в девять раз

ит.д. (на это указывают квадратные корни в уравнении прямой). Ясно, однако, что наша людоедская модель сильно идеализирована

ибыло бы опасно прямо применять её к реальной ситуации. Возникнет вопрос — как изменится вывод, если модель будет несколько иной. Например, коэффициенты а и b могут быть не строго постоянными, а могут, скажем, зависеть от х и от у. И точный вид этой зависимости нам может не быть известен. В этом случае речь идет о системе

x! = а(x, y)x y! = b(x, y) y

которая уже не решается явно.

Однако в математике разработаны топологические методы( см.Главу 6), позволяющие сделать выводы общего характера и не зная точно явного вида функций а и b. В этой ситуации принято говорить о мягкой модели — модели, поддающейся изменениям (за счет выбора функций а и b в нашем примере).