Добавил:

fench Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Нагорнов Обратные задачи палеотермометрии 2008

.pdf

Скачиваний:

Добавлен:

16.08.2013

Размер:

1.82 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 188 9 10 11 12 13 14 15 16 17 18 > Следующая >>>

k	Ui 1 2Ui Ui 1
	i	h2		(5.3)
ki 1 ki 1 Ui 1 Ui 1				(5.3)
ki 1 ki 1 Ui 1 Ui 1			0,	i 1, 2,...N 1.
	2h	2h
	Разностная аппроксимация граничного условия на поверхно-
сти:
U0 Us .				(5.4)

Запишем разностную аппроксимацию граничного условия на глубине H со вторым порядком точности по координате. Для этого рассмотрим разностную аппроксимацию первой производной в точке

zN :	UN UN 1		. Раскладывая		UN 1 в ряд Тейлора в окрестности

	h
точки zN , получим:
UN UN 1		dU		(H ) h d 2U	(H ) O(h2 ) .	(5.5)
h		dz		2 dz2

Используя дифференциальное уравнение из задачи (5.1), получаем:

UN UN 1 dU				(H )
	h		dz
h	1	dk	(H ) dU (H ) O(h2 ) .				(5.6)
h			(H ) dU (H ) O(h2 ) .				(5.6)
2 k(H ) dz				dz
Тогда:					1
dU (H )		1	kN kN 1		1	UN UN 1 O(h2 ) .	(5.7)
dz				2kN		h
dz				2kN		h

Следовательно, граничное условие на глубине H в разностной форме имеет вид:

U	N	U	N 1	qh(3kN kN 1 )	.	(5.8)

				2kN2

Таким образом, разностная аппроксимация задачи для стационарного температурного профиля в горных породах (5.1) может быть записана в следующем виде:

Z0 0Z1 0 ;

Ai Zi 1 Ci Zi Bi Zi 1

Fi ,

i 1, 2,...N 1;

(5.9)

ZN N ZN 1 N ,

где: A 1

ki 1

, B 2 A ,

C 2 ,

F 0 ,

(5.10)

4ki

qh(3kN kN 1)

0 , U

(5.11)

2kN2

Матрица системы линейных алгебраических уравнений (5.9) является трехдиагональной, тогда для решения этой задачи воспользуемся методом прогонки [Самарский, 1971]. Метод прогонки состоит из трех шагов:

1. Прямая прогонка

Ai i 1 Fi

i 1...N 1.

(5.12)

Ci Ai i 1

Вычисление решения на последнем шаге

N N 1 N .

(5.13)

1 N N 1

Обратная прогонка

Zk k Zk 1

k ,

k N 1...0 .

(5.14)

Рассмотрим численное решение задачи (5.2) для остаточного температурного профиля V(z,t) . Запишем разностную аппроксима-

цию второго порядка точности по координате и первого порядка точности по времени для дифференциального уравнения из этой за-

дачи в области [0, H ], [0,t f ] :

c	V j 1	V j	k	V j 1	2V j 1	V j 1	V j	2V j V j
c	i	i	k	i 1	i	i 1	i 1	i i 1
i i			i			2h2

i 1

V j 1

V j

i 1

(5.15)

i 1, 2,...N 1,

j 0, 2,...M 1 .

В случае,

когда

k(z) const ,

данная аппроксимация будет иметь

второй порядок точности по времени.

Разностная аппроксимация граничного условия на поверхно-

сти:

V j 1	j 1,	j 0, 2,...M 1.	(5.16)
0

Запишем разностную аппроксимацию граничного условия на глубине H со вторым порядком точности по координате и вторым порядком точности по времени. Для этого рассмотрим разностную аппроксимацию первой производной по координате в точке

) :

V j 1 V j 1

в ряд Тейлора, в окрестно-

j 1

N 1 . Раскладывая V j 1

N 1

сти точки (zN ,t j 1) получим:

V j 1

(H ,t

)

(H ,t

) O(h2 ) .

(5.17)

N 1

j 1

Используя дифференциальное уравнение из задачи (5.2), получаем:

V j 1	V j 1	V	(H ,t j 1)	h 1	dk	(H )	V	(H ,t j 1)
N	N 1
		z		2 k(H ) dz			z
	h

h	(H )c(H ) V	(H ,t j 1 ) O(h2 ) .	(5.18)

	k(H ) t
2

Тогда

V (H ,t			j 1	)	1 kN kN 1			1
z						2kN

	j 1			j 1		N cN	j 1			j
VN		VN 1			h		VN		VN		O(h2 , 2 ) .

		h			2	kN

Следовательно, граничное условие на глубине H имеет вид:

(5.19)

в разностной форме

V j 1	1	h2	N cN	1 V j 1

N		2	kN		N 1

h2	N cN	1	h2	N cN	1 V j ,		j 0, 2,...M 1.	(5.20)
		1			1 V j ,		j 0, 2,...M 1.	(5.20)
2	kN		2	kN		N
2	kN		2	kN
							73

Разностная аппроксимация начального условия:

Vi0 0, i 0,1,...N .

Таким образом, разностная аппроксимация задачи для остаточного температурного профиля в горных породах (5.2) на каждом

последующем j 1-м шаге по времени может быть записана в виде

(5.9), где:

Ai 1 ki 14kiki 1 , Bi 1 ki 14kiki 1 , Ci 2 1 kici i h2 ,

F AV j (4 C )V j

BV j

(5.21)

i 1

i i 1

0 , j 1 ,

N cN

1 V j ,

(5.22)

и решена методом прогонки.

6. РЕШЕНИЕ ЗАДАЧИ РАСПРОСТРАНЕНИЯ ТЕПЛА В ГОРНЫХ ПОРОДАХ С ПОСТОЯННЫМИ СВОЙСТВАМИ СРЕДЫ

В большинстве случаев физические свойства горных пород, такие как плотность, удельная теплоемкость и теплопроводность, являются практически постоянными по всей глубине скважины, то-

гда (z) , c(z) c и k(z) k . Следовательно, задача для стационарного температурного профиля U (z) (4.40) в однородных горных породах будет выглядеть следующим образом:

d 2U (z) 0, z (0, H ) ; dz2

U (0) Us ;		(6.1)
dU	(H ) q .
dz		k

Несложно установить, что решение этой задачи будет следующим:

U (z) Us q z .	(6.2)
k

Таким образом, стационарный температурный профиль в горных породах является линейной функцией глубины.

Запишем задачу для остаточного температурного профиля V(z,t) (4.41) в однородных горных породах:


	V (z,t)		a2 2V (z,t)	, z (0, H ),t (0,t	f	];
	t		z2		f
V (0,t) (t) ;
	V	(H ,t) 0 ;				(6.3)
		(H ,t) 0 ;				(6.3)
	z

V (z,0) 0 ,

здесь a2 kc – коэффициент температуропроводности.

Будем искать остаточный температурный профиль V(z,t) в

виде: V(z,t) (t) V(z,t),

(6.4)

где V(z,t) – решение следующей задачи:

		(z,t) a2	2		(z,t)	f (t), z (0, H ),t (0,t		]
	V	(z,t) a2	V		(z,t)	f (t), z (0, H ),t (0,t	f	]
	t			z2			f
V (0,t) 0 ,
	V	(H ,t) 0 ;						(6.5)
	z	(H ,t) 0 ;						(6.5)
	z

V (z,0) 0 ,

где f (t) d dt(t) .

Будем искать решение данной задачи в виде ряда Фурье по собственным функциям соответствующей однородной задачи [Тихонов, Самарский, 1977]. Разделив переменные в однородной задаче, получим следующую задачу Штурма-Лиувилля на собственные функции и собственные значения:

d 2	0;	(0) 0;	d	(H ) 0 .	(6.6)
dz2			dz

Собственные функции задачи (6.6) имеют вид:

n (z) sin(

n z)

(n 1, 2,3,...) ,

а собственные значения:

n 1 2 2n 22 .

Таким образом, получим решение задачи (6.5):

d ,

V(z,t) In n (z) f ( )e

(t )

n 1

где

H n (z)dz

(6.7)

(6.8)

(6.9)

(6.10)

Соответственно, решением задачи (6.3) на конечный момент времени t f , с учетом того, что (0) 0 , будет:

	tf	2
V(z,tf ) (tf ) In n (z) (tf ) na2	( )e a		n (tf )d . (6.11)
	0
n 1
n 1

7. АЛЬТЕРНАТИВНАЯ ПОСТАНОВКА ЗАДАЧИ РАСПРОСТРАНЕНИЯ ТЕПЛА В ГОРНЫХ ПОРОДАХ С ПОСТОЯННЫМИ СВОЙСТВАМИ СРЕДЫ

В связи с тем, что в горных породах измеренный температурный профиль и стационарный температурный профиль, начиная с некоторой глубины, совпадают, а остаточный температурный профиль, начиная с этой глубины, равен нулю. Таким образом, от зада-

чи (6.3) на ограниченной прямой [0, H ], можно перейти к задаче на

полубесконечности:
V (z,t)	a2 2V (z,t)	, z (0, ),t (0,t	f	];
t	z2		f
V (0,t) (t) ;				(7.1)

V (z,0) 0 .

Решение этой задачи для произвольного изменения температуры на поверхности (t) дается следующей формулой [Тихонов,

Самарский, 1977]:

t f

4a2

(t f )

V(z,tf )

( )d .

(7.2)

3/2

0 a

(tf )

Представим изменение температуры на поверхности

(t) в

виде кусочно-постоянной функции:

0 ,

t0 0 t t1

1 ,

t1 t t2

(7.3)

(t)

..............................

, tM 1 t tM t f

M 1

Тогда решение задачи (7.1) может быть записано следующим образом:

M 2
V (z,t f )	i (z,t f ti ) (z,t f ti 1 )	,	(7.4)
i 1		,	(7.4)

M 1 (z,t f tM 1)

		z		2
					e	2
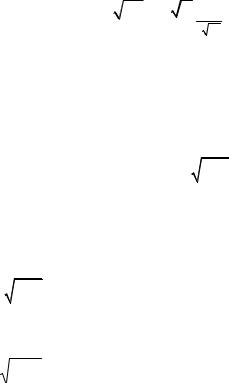
где: (z,t) 1 erf							d .	(7.5)
	2	2
		a	t		z

2 a2t

Оценим глубину проникновения температурного возмущения на поверхности за время t. Предположим, что в начальный момент времени, равный нулю, произошло мгновенное изменение температуры на величину D. В этом случае решение (7.4) будет записано в виде:

V (z,t f ) D (z,t f

) D 1 erf

(7.6)

a2t

Видно, что глубина, на которую проникло

% амплитуды скачка

температуры на поверхности за время t f ,

определяется из следую-

щего соотношения:

erf (

) 1

(7.7)

a2t f

100%

Следовательно, глубина,

на которую проникло 0.5%

амплитуды

скачка температуры на поверхности за время t f , будет следующим:

z 4 a 2t f .

(7.8)

Таким образом, при обычном значении температуропроводности ( a2 10 6 м2 /с), скважина глубиной 500 м зафиксирует со-

бытия, произошедшие не ранее 500 лет назад, километровая – не ранее 2000 лет назад, а двухкилометровая 8000 лет назад. Более подробно зависимость длительности истории изменений температуры поверхности, зафиксированной в скважине, от ее глубины для

a2 10 6 м2 /с можно видеть на рис. 7.1.

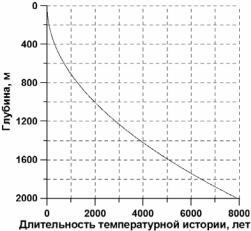
Рис. 7.1. Зависимость длительности истории изменений температуры поверхности, зафиксированной в скважине, от ее глубины для обычного значения

температуропроводности

<<< < Предыдущая 1 2 3 4 5 6 78 / 188 9 10 11 12 13 14 15 16 17 18 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.08.20138.57 Mб193Мишулина Лабораторный практикум по курсу 2007.pdf
#
16.08.20133.86 Mб116Мишулина Основы теории вероятностей 2011.pdf
#
16.08.20131.36 Mб102Мосолов Изучение универсалного метода проектирования 2010.pdf
#
16.08.20131.95 Mб78Набойченко Техника реакторного експеримента 2008.pdf
#
16.08.20133.07 Mб491Нагорнов Вейвлет-анализ в примерах 2010.pdf
#
16.08.20131.82 Mб32Нагорнов Обратные задачи палеотермометрии 2008.pdf
#
16.08.2013696.72 Кб334Наумов Моделирование нестационарных и аварийных 2007.pdf
#
16.08.20131.71 Mб59Нечаев Моделирование процессов ядерной технологии 2007.pdf
#
16.08.20132.03 Mб117Никитин Шемотехника интегралных шем ТТЛ, ТТЛШ и КМОП 2010.pdf
#
16.08.20131.14 Mб50Никифоров Взаимосвяз открытых систем 2010.pdf
#
16.08.2013645.64 Кб30Нормы радиационной безопасности (НРБ-99) 1999.pdf