Нагорнов Вейвлет-анализ в примерах 2010

……………………………………………………….…………………

Каждая строка условно поделена на две части. Очевидно, правая часть каждой строки будет фильтром высоких частот.

Для удобства обозначим элементы полученного массива как показано ниже:

………………………………

………………………………

Вновь произведем операции, аналогичные вышеприведенным, но со столбцами:

………………..……………………………………………

………………..……………………………………………

……………………………………………………………….

………………..…………………………………………...…

111

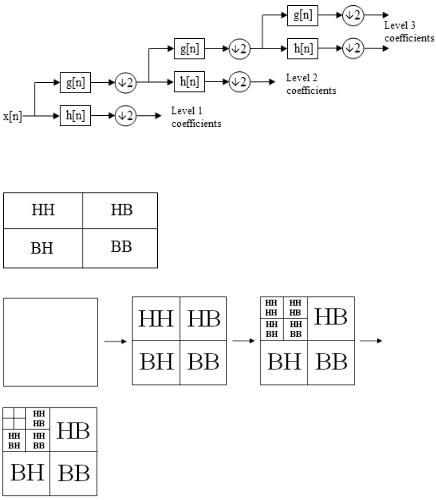
Каждый столбец условно поделен на две части. Нижняя часть – фильтр высоких частот. Механизм условно представлен на схемах рис. 6.4–6.6.

Рис.6.4. Схема вейвлет-декомпозиции изображения, где h[n] – фильтр высоких частот, g[n] – фильтр низких частот

Рис. 6.5. Схема вейвлет-разложения изображения на частотные диапазоны: Н – фильтр низких частот, В – фильтр высоких частот

Рис. 6.6. Схема вейвлет-преобразования изображения: Н – фильтр низких частот, В – фильтр высоких частот

Количество итераций =log2[min(M ; N)], где M и N – количест-

во строк и столбцов соответственно. В результате всех итераций будет получен массив вейвлет-коэффициентов, после чего можно составлять вейвлет-признаки.

112

6.5. Математическое описание и физический смысл вейвлет-признаков

Для обобщенной характеристики полученного массива вейвлеткоэффициентов применяют вейвлет-признаки. В качестве примера таковых приведем следующие:

коэффициентов. Физический смысл – энергия. Если вейвлеткоэффициенты меньше единицы, то их энергия (сумма квадратов) будет меньше суммы вейвлет-коэффициентов;

energy_re ={∑nk =1(X12 +... + Xk2 )}−1 ;

max =maxk ( Xk ), максимальный среди вейвлет-коэффициен-

тов. Физический смысл – граница, за которую значения вейвлеткоэффициентов не переходят

max_re ={maxk ( Xk )}−1 ;

range =maxk ( Xk ) −mink ( Xk ) разница между максимальным и

минимальным среди вейвлет-коэффициентов. Физический смысл – диапазон изменения вейвлет-коэффициентов

range_re ={maxk ( Xk ) −mink ( Xk )}−1 ;

тическое среди вейвлет-коэффициентов. Физический смысл – математическое ожидание или среднее значение вейвлеткоэффициентов

113

Физический смысл – наиболее вероятный предел колебаний вейв-

формул используется развертка двухмерного массива в числовой ряд)

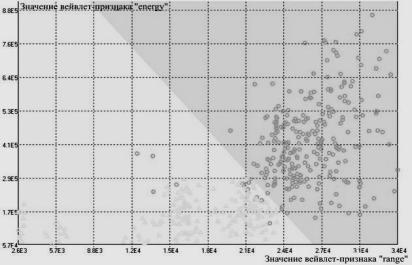
Ниже приведены результаты расчета признаков «energy» и «range» для анализируемой выборки изображений клеток крови.

Рис. 6.7. Визуализация распределения клеток исследуемой выборки в пространстве вейвлет-признаков «energy» и «range»

На рис. 6.7 в двухмерном пространстве признаков energy и range представлено распределение клеток исследуемой выборки, содержащей бласты и лимфоциты, на рис. 6.8 показана гистограмма. Применение линейного классификатора в рассматриваемом

114

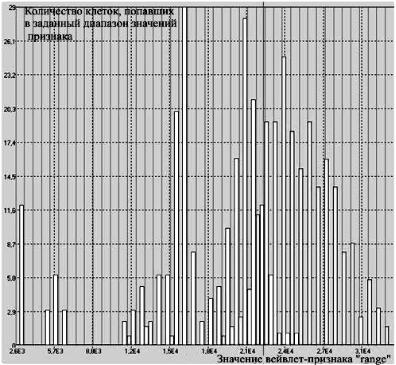
случае дает в результате ошибочную классификацию для 12 бластов и для 4 лимфоцитов, что в сумме составляет (12 + 4)/390 = 6 % .

Таким образом, применение вейвлет-преобразований является эффективным инструментом в решении широкого круга задач анализа и классификации изображений и одномерных функций.

Рис. 6.8. Гистограмма распределения клеток исследуемой выборки по значениям признака «range»

115

СПИСОК ЛИТЕРАТУРЫ

1.Burt P., Adelson E. The Laplacian pyramid as a compact image code // IEEE Trans. Comm., 31. P. 482–540.

2.Chui C.K. Wavelets: a tutorial in theory and applications // Academic Press, 1992.

3.Daubechies I. Ten Lectures on Wavelets // SIAM, 1992.

4.Foster, G. Wavelets for Period Analysis of Unequally Sampled Time Series // Astronomical Journal, 1996, 112(4), 1709–29.

5.IEEE Trans. on Information Theory, Vol. 38, № 2, March 1992 (специальный номер по вейвлетам).

6.Smith M., Barnwell T. Exact Reconstruction Techniques for Tree-Structured Subband Coders // IEEE Trans. on ASSP, v. ASSP-34,

№3, June 1986.

7.Misiti M., Misiti Y., Oppenheim G., J.-M. Poggi. Wavelet Toolbox. For use with MATLAB. User’s Guide // The MathWorks, Inc. – http://www.mathworks.com. 2002.

http://support.sibsiu.ru/MATLAB_RU/wavelet/book3/index.asp.htm.

10.Астафьева Н.М. Вейвлет-анализ: Основы теории и примеры применения // Успехи физических наук, 1996, т.166, № 11. С. 1145– 1170.

11.Витязев В.В. Вейвлет-анализ временных рядов. СПб.: 2001.

12.Воробьев В.И., Грибунин В.Г. Теория и практика вейвлет преобразования // ВУС, 1999. С.1–204.

13.Давыдов А.В. Вейвлетные преобразования сигналов. [Электронный ресурс] : [курс лекций для вузов ] // Вейвлеты. – 2009.

14.Дьяконов В., Абраменкова И. MATLAB. Обработка сигналов и изображений. Специальный справочник. СПб.: Питер, 2002.

15.Илюшин. Теория и применение вейвлет-анализа. – http://atm563.phus.msu.su/Ilyushin/index.htm.

16.Кирьянов Д.В., Сапонов Д.И. Вейвлет-спектры ионосферного радиосигнала // Тезисы конференции Ломоносов-99. М.:МГУ, 1999.

17.Киселев А. Основы теории вейвлет-преобразования. – http://www.basegroup.ru/library/cleaning/intro-to-wavelets/

116

18.Козлов П.В., Чен Б.Б. Вейвлет-преобразование и анализ временных рядов // Вестник КРСУ, 2002, № 2.

19.Левкович-Маслюк Л., Переберин А. Введение в вейвлетанализ.

20.8-я Международная конференции по компьютерной графике

ивизуализации ГрафиКон'98. – М.: ГрафиКон’98, 1998.

21.Никитаев В.Г. и др. Компьютерные системы гематологической диагностики. Введение: Учебное пособие. М.: МИФИ, 2006.

22.Новиков Л.В. Основы вейвлет-анализа сигналов: Учебное пособие. – СПб, ИАНП РАН, 1999, 152 с.

23.Переберин А.В. О систематизации вейвлет-преобразований // Вычислительные методы и программирование, 2002. Т. 2. С. 15– 40.

24.Сонечкин Д.М., Даценко Н.М., Иващенко Н.Н. Оценка тренда глобального потепления с помощью вейвлетного анализа // Изв. РАН. Физика атмосферы и океана. – 1997. Т. 33. № 2. С. 184– 194.

117