
Борман Теория разделения изотопов 2007
.pdf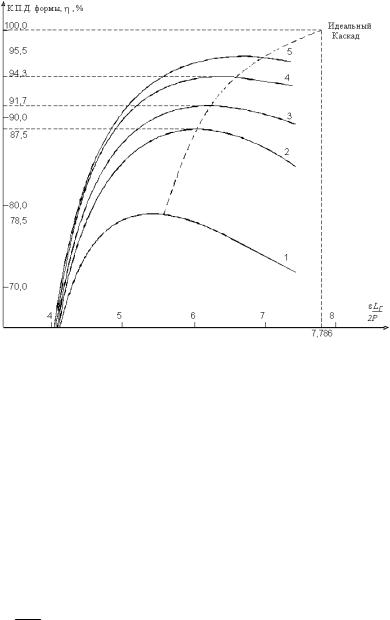
Рис. 1.24. Зависимость КПД формы от относительной величины головного потока ПСК при различных числах секций в каскадах, приведенных на рис. 1.23 [4]
c* = |
|
cP |
. |
(1.257) |
|
εLi |
|||
1+ |
|
|
||
2P(σi +1) |
|
|
||
Заметим, что при выполнении соотношения (1.251) параметрами оптимизации становятся головной поток прямо- угольно-секционированного каскада (ПСК) – LГ (или отно-
шение головного потока идеального каскада L*(cF ) к головному потоку ПСК – LГ ) и коэффициенты ступенчатости
σi = LLi . i+1
111
На рис. 1.24 представлены зависимости КПД формы ПСК от головного потока LГ при различных значениях чисел сек-
ций. Каждому значению головного потока LГ на зависимостях 1-5 соответствует максимальное значение величины
КПД формы при оптимизации по переменным σi = |
Li |
. |
|
||
|
Li+1 |
|
В свою очередь, каждая кривая η = f (LГ ) на рис. 1.24 |
про- |
|
ходит через максимум. Эти точки экстремума и сами экстремумы соответствуют абсолютному максимуму величины η и,
соответственно, определяют оптимальный вариант ПСК с заданным числом прямоугольных секций. С ростом числа секций максимумы η = f (LГ ) становятся более пологими, а при
бесконечном увеличении числа секций КПД прямоугольносекционированных каскадов стремится к 100%.
1.10.ПК в случае произвольных обогащений на его ступенях [27]
В случае немалых обогащений на ступенях ПК (рис. 1.25) с математической точки зрения представляет дискретную систему, к которой не приемлемы подходы и допущения, имеющие место для каскадов с малыми обогащениями на его ступенях.
По определению прямоугольного каскада на входе в каждую ступень поток одинаков, т.е. Ls = L = const, 1 ≤ s ≤ N .
Для выполнения этого условия в общем случае на концах каскада организуется закрутка в виде подачи части потока, выходящего с крайних ступеней в их питание
′′ |
|
′′ |
|
|
|
T3 |
′ |
= L1 |
−W1 |
(1.258) |
|
T |
′ |
− P |
. |
||
|
= L |
|
|
||
3 |
n |
|
|
|
|
112
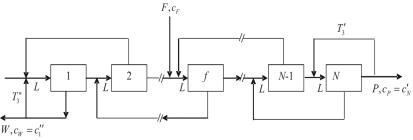
Рис. 1.25. Схема прямоугольного каскада |
|
|||||||
Для обогатительной части каскада: |
|
|||||||
|
|
θs L − (1−θs+1)L = P , |
(1.259) |
|||||
|
θsLc′s −(1−θs+1)Lc′′s+1 = PcP . |
(1.260) |
||||||
Для обеднительной части каскада эти уравнения справед- |
||||||||
ливы, нужно только заменить P → −W , cP → cW . |
|
|||||||
Из этих формул следует |
|
|
|
|
||||
θs+1 =1−θs −WL , s = 2,K, f −1; |
(1.261) |
|||||||
|
|
|
|
|
|
P |
|
|
|
θ |
|
=1−θ |
|
+ |
, s = f ,K, N. |
|
|
s+1 |
s |
|
|
|||||
|
|
|
|
L |
|
|||
|
|
|
|
|
|
|
||
Рассмотрим способы задания коэффициентов деления потока θs в прямоугольном каскаде (см. рис.1.25) [27, 28]. Ра-
венство L=const налагает определенные условия на выбор θs . Общим для всех способов задания θs является периодическое
повторение через ступень по всей длине каскада «базового» коэффициента деления потока, имеющего место на ступени с номером f.
Первый способ задания коэффициента деления потока состоит в том, что все коэффициенты в обеднительной (отвальной) части каскада равны «базовому», в обогатительной (отборной) части базовый коэффициент периодически повторяется через ступень:
113
θs = |
1 |
|
− |
W |
|
, |
где |
s =1,2, ... , f |
и s = f + 2, f + 4, ... |
|||
2 |
1 |
L |
|
|||||||||
|
|
|
|
|
|
|
|
|
(1.262) |
|||
|
|
|
|
1 |
|
|
|
W |
|
F |
|
|
|
θs = |
|
|
+ |
, где s |
= f +1, f +3, ... |
||||||
|
2 |
1− |
|
L |
||||||||
|
|
|
|
|
|
|
L |
|
|
|
||
Во втором способе наоборот, коэффициенты деления потока периодически меняются в отвальной части, а в отборной равны между собой
|
1 |
|
|
P |
|
|
|
|
|
|
|
|
θs = |
|
1 |
+ |
|
, где s = f , f +1, ... , N и s = f −2, f −4, ... , |
|||||||
2 |
L |
|||||||||||
|
|
|
|
|
|
|
|
|
(1.263) |
|||
|
|
|
|
|
1 |
|
|
P |
|
F |
||
|
|
θs = |
+ |
− |
, где s = f −1, f −3, ... |
|||||||
|
|
2 |
1 |
|
L |
|||||||
|
|
|
|
|
|
|
L |
|
|
|||
И, наконец, общий способ задания коэффициента деления потока состоит в следующем. Задают для разных ступеней следующие коэффициенты деления потока
θs |
=θ f , s = ..., |
f |
−4, f −2, f , |
f + 2, f + 4, ... |
|
|||||||
|
θ |
s |
=1−W −θ |
f |
, |
s = f −1, |
f −3, ... , |
(1.264) |
||||
|
|
|
|
|
L |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
θ |
|
=1+ |
P |
−θ |
|
, |
s = f +1, |
f +3, ... , |
|
||
|
s |
|
f |
|
||||||||
|
|
|
|
|
L |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
где 0 <θ f |
|
− |
W |
|
|
|
|
|
|
|||
< 1 |
L |
– величина базового коэффициента, зада- |
||||||||||
|
|
|
|
|
|
|
|
|
||||
ваемая, например, из соображений гидродинамической устойчивости каскада. Как нетрудно убедиться, первые два из описанных методов являются частными случаями третьего.
Если потребовать равенство θ в двух соседних ступенях и
|
F |
|
внешнее питание подавать в равных долях |
|
в обогащен- |
|
||
|
2 |
|
ный поток f −1-й ступени и в обедненный поток f -й ступе-
114
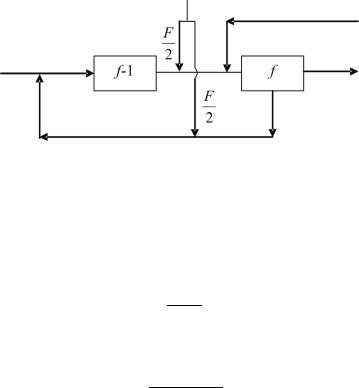
ни (см. схему на рис. 1.26), то в этом случае приходим к следующим формулам,
|
|
1 |
|
|
W |
|
≤ s ≤ |
f −1; |
||
|
|
|
1− |
|
, 1 |
|||||
θ |
|
2 |
|
|
L |
|
|
(1.265) |
||
s |
= |
1 |
|
|
P |
|
|
|||
|
|
+ |
|
f ≤ s |
≤ N. |
|||||
|
|
|
2 |
1 |
|
|
, |
|||
|
|
|
||||||||
|
|
|
|
|
L |
|
|
|
||
Рис. 1.26. Схема деления внешнего потока питания
Получим теперь формулы для расчета распределения концентрации по длине каскада. По определению полного коэффициента разделения ступени имеем:
c'
q = |
|
1− c' |
|
, |
(1.266) |
|
|
|
|||
|
|
c" |
|
||
1− c"
откуда концентрация ценного (целевого) компонента в обогащенном потоке будет равна
c ' = |
qc " |
|
1+(q −1)c " . |
(1.267) |
В дальнейшем принято, что величина q по ступеням каскада не меняется.
Из балансовых уравнений (1.259) с учетом (1.266) и (1.267) следует
115
|
" |
|
|
θs |
|
|
q cs" |
|
Wc1" |
|
|
|
|
||
cs+1 |
= |
|
|
|
|
|
+ |
|
|
|
|
, s < f ; |
|
||
1−θ |
s+1 |
1+(q −1)c" |
(1−θ |
s+1 |
)L |
|
|||||||||
|
|
|
|
|
|
s |
|
|
|
|
|
|
|||
|
|
|
|
θs |
|
|
q cs" |
+Wc1" − FcF |
|
(1.268) |
|||||
c" |
= |
|
|
|
, s ≥ f . |
||||||||||
|
s+1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1−θ |
s+1 |
1+(q −1)c" |
|
(1+θ |
|
)L |
|
|
||||||
|
|
|
|
|
|
s |
|
|
|
s+1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Чаще всего задачу поверочного расчета прямоугольного каскада формулируют следующим образом.
Задано: N, f , q, cF , P, W, F, L . Найти cP и cW , возможно и cs , а также распределение θs по длине каскада. Та-
кой расчет необходим при исследовании оптимального управления процессом разделения при изменении режимов работы отдельных ступеней разделительного каскада, а также при использовании одного и того же каскада для разделения различных изотопных смесей. Сложность такого расчета связана с нелинейностью уравнений (1.268), а также с тем фактом, что значения концентраций на концах каскада, явно входящие в эти уравнения, неизвестны.
Невозможность аналитического решения системы (1.268) приводит к необходимости разработки и использования численных итерационных методов с уточнением ориентировочно принятых начальных значений концентраций на концах каскада (см. часть 2).
Соотношения (1.259) – (1.260) и (1.268) и соответственно алгоритм расчета могут быть легко обобщены на случай ПСК.
Задачу оптимизации ПК можно сформулировать следующим образом. Пусть величины P, cP, cF , cW , q заданы, то-
гда количество свободно выбираемых переменных каскада составляет 3 параметра. Это дискретные параметры N (полное число ступеней в каскаде), f (номер ступени, на вход которой подают поток питания F ) и величина потока пита-
116
ния ступеней L = const . Значения N, f и L должны быть
найдены в результате решения задачи оптимизации. В качестве критерия оптимизации может быть выбран минимум суммарного потока.
1.11. Нестационарные (переходные) процессы в каскадах
1.11.1.Дифференциальное уравнение нестационарного разделительного процесса. Некоторые особенности нестационарных процессов [29, 30]
Одной из специфических особенностей получения стабильных изотопов (особенно в случае «слабого обогащения», реализующегося в методе газовой диффузии, а также в физи- ко-химических методах: дистилляции, химическом изотопном обмене) является большая длительность переходных процессов в разделительных каскадах, измеряемая в ряде случаев неделями и даже месяцами, что может быть сравнимо с длительностью непрерывной работы установки.
Одной из основных целей исследовании нестационарных (переходных) процессов в каскадных установках является определение характерного «времени установления», т.е. времени от запуска каскада до достижения величин внешних потоков и концентраций, соответствующих стационарному режиму установки. Этот режим имеет место в том случае, когда в каждом сечении каскада перенос (поток) ценного изотопа Js
равен PcP для обогатительной и WcW для обеднительной
частей каскада соответственно. При этом стационарный режим течения разделяемой смеси устанавливается сравнительно быстро, тогда как стационарный режим по концентрациям в случае q ~1 достигается за существенно более длительное
время.
Для получения уравнений, описывающих нестационарный процесс переноса ценного компонента в каскаде в случае
117
«слабого обогащения», рассмотрим каскад для разделения бинарной смеси изотопов однофазным методом. Пусть в некоторое промежуточное сечение каскада подают поток питания F, а с концов каскада отбирают потоки отбора P и отвала W. Величины P, W и F в общем случае могут быть функциями от времени, но при этом должны быть связаны уравнением сохранения вещества (F = P +W ) . Предположим, что режим
гидродинамических течений в каскаде установился и потоки, а также количество разделяемого вещества на каждой ступени («задержка») H(s) не зависят от времени. Ниже будет по-
казано, что такое предположение допустимо при разделении изотопов. С учетом сделанных предположений запишем условия материального баланса в произвольном сечении каскада на участке между s-й и s + 1 ступенями
L′(s) − L′′(s +1) = T (s) , |
(1.269) |
L′(s) C′(s,t) − L"(s +1) C"(s +1, t) = J (s, t) , |
(1.270) |
где T (s) – перенос (поток) разделяемого вещества, |
J (s,t) – |
перенос (поток) ценного (извлекаемого) изотопа.
В обогатительной части каскада перенос T равен величине потока отбора, а в обеднительной части – величине потока отвала со знаком минус. Поток J (s,t) определяется накопле-
нием ценного компонента в различных частях каскада:
– в обогатительной части
S |
∂ |
[H (i) c(i,t)], |
|
|||
J (s,t) = P c(s,t) + ∑ |
(1.271) |
|||||
|
|
|||||
i=s+1 |
∂t |
|
|
|||
– в обеднительной части |
|
∂ |
|
|
||
S |
|
|
|
|||
J (s,t) = −W c(1,t) + ∑ |
|
[H (i) c(i,t)], |
(1.272) |
|||
|
|
|
||||
i=s+1 ∂t |
|
|
||||
где s = 1 и s = S – номера первой и последней ступеней каскада соответственно.
Для рассматриваемого случая «слабого обогащения» с точностью до малых порядка ε2 система разностных уравне-
118
ний (1.269), (1.270) с учетом (1.271) и (1.272) может быть приведена к уравнению в частных производных
H (s) |
∂c(s,t) |
= − |
∂ |
J (s,t) , |
(1.273) |
|
∂t |
∂s |
|||||
|
|
|
|
где выражение для потока ценного изотопа определяется как
|
L(s) |
|
∂c |
|
|
||
J (s,t) = |
|
εc(1 |
− c) − |
|
+T c . |
(1.274) |
|
2 |
|||||||
|
|
|
∂s |
|
|
||
В однофазных методах разделения разделительные каскады, как правило, имеют одинаковые элементы. Это позволяет полагать, что задержка ступени прямо пропорциональна по-
току L(s) [1], т.е.
H(s) =ωL(s) , |
(1.275) |
где ω – коэффициент пропорциональности, имеющий размерность времени. Величина ω определяет время, на которое задерживается разделяемое вещество в ступени. При этом
время, равное ω / ε 2 , по порядку совпадает с продолжительностью переходных процессов, связанных установлением потока L(s). А время достижения равновесных распределений концентраций характеризуется, как будет показано ниже,
временем h /ε 2 . Учитывая, что число ступеней в каскаде об-
ратно пропорционально величине ε , очевидно, что временем установления Nh можно пренебречь и полагать H и L функциями только номера ступени.
Если ввести новые переменные
y = εs, τ = |
ε2t |
, χ = |
εL |
, |
(1.276) |
|
2ω |
2 |
|||||
|
|
|
|
то после этого такие характеристики разделительного процесса, как ε и ω , из описания нестационарного процесса могут быть исключены, а исходная система (1.273), (1.274) примет вид, не зависящий от конкретного метода разделения
119
|
∂c |
|
|
1 ∂ |
|
∂c |
|
|
|
|
P |
|
|
|
|||||
|
|
= − |
|
|
|
|
|
χ |
− |
|
+c(1 |
−c) + |
|
|
c |
, |
(1.277) |
||
|
|
|
|
|
|
|
|
||||||||||||
|
∂τ |
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
χ |
|
|
|
|
|
|
χ ∂y |
|
|
|
|
|
|
|
|||||||||
для обогатительной части каскада, и |
|
|
|
|
|
|
|
||||||||||||
|
∂c |
|
|
1 ∂ |
|
∂c |
|
|
|
W |
|
|
|
||||||
|
|
= − |
|
|
|
|
|
|
χ |
− |
|
+c(1 |
−c) − |
|
|
c |
, |
(1.278) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
∂τ |
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
χ |
|
|
|
|
|
|
χ ∂y |
|
|
|
|
|
|
|
|||||||||
для обеднительной части каскада.
В уравнениях (1.273) и (1.277) в приближении «слабого обогащения» предполагается, что отсчет ступеней каскада проводится от отвала к отбору, т.е. от y = 0 до y0 = εS . В
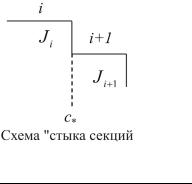
граничные условия кроме условий на концах каскада должны входить условия на стыках соседних секций .
Связь уравнений нестационарного процесса в точке «стыка» соседних i-й и (i + 1)-й секций можно получить из усло-
вий сохранения переноса в этом сечении |
|
||||||||||
т.е. |
|
|
|
|
|
Ji |
= Ji+1 , |
|
(1.279) |
||
|
∂c − |
|
|
|
|
+ |
|
|
|
|
|
χ |
|
+ χ |
|
|
∂c |
|
− χ |
)c |
(1−c ) = 0 , (1.280) |
||
|
|
|
|
|
−(χ |
|
|||||
|
i |
∂y |
|
i+1 |
|
∂y |
|
i |
|
i+1 * |
* |
где знаки – и + обозначают производную слева и справа от «стыка» i-й и (i + 1)-й секций, а c* – концентрации в точке «стыка» секций.
Если на стыке k -й и k +1-й секции подают поток питания F , то уравнение (1.280) с учетом уравнения баланса разделяемого вещества по каскаду:
F = P +W |
(1.281) |
Под секцией в общем случае следует понимать участок каскада, на котором функция χ( y) является непрерывной функций координаты.
120
