Башуров Методика решения математических задач 2011

Поскольку любая элементарная функция выражается при помощи операций сложения, вычитания, умножения, деления и суперпозиции через простейшие элементарные функции, то, используя только вышеприведенные формулы, можно взять производную от любой элементарной функции. Для этого достаточно знать таблицу производных от простейших элементарных функций:

′1 11) (arcctg x)′ = −1 + x2 .

6)(tg x) = cos2 x ;

′1

7)(ctg x) = −sin2 x ;

Вслучае если функция не элементарна, то для взятия производной остается только одно – найти (если он существует) предел1

Если мы рассматриваем функцию двух и более переменных, то

вместо производной рассматриваются частные производные. Определение 3.3. Частной первой производной функции

z = f(x1,x2,…,xn) от n переменных по переменной xk в точке x10 ,..., xn0

называется предел (если он существует)

Согласно определению, техника и приемы взятия частных производных точно такие же, что и при взятии обыкновенной производной. Например, вычисляя производную по x1, остальные переменные x2, …, xn рассматривают как постоянные.

31

Обозначение: ∂z или z′x .

∂xk k

Частные производные от частных первых производных носят

∂2 z

название вторых частных производных и обозначаются ∂xk ∂xm .

Ответ на вопрос о том, при каких условиях значения смешанных производных не зависят от того, в каком порядке производится дифференцирование, дает следующая теорема (для функций двух переменных).

Теорема 3.1. Если производные ∂2 z и ∂2 z функции z = f(x,y),

∂x∂y ∂y∂x

определенной в окрестности точки М существуют в некоторой δ-окрестности точки М(x,y) и непрерывны в самой точке, то они равны между собой в этой точке.

Порядок взятия вторых частных производных неважен! Это оз-

Точно так же, как и второй дифференциал функции одного переменного, определяется и второй дифференциал функции многих переменных. При этом дифференциалы независимых переменных выступают в роли констант, например:

f(x1, x2, …, xn) = 0, то сначала рассматривают все частные производные по всем переменным от функции f(x1, x2, …, xn) в точке

32

(x10 ,..., xn0 ) . Затем следует решить, какую из переменных x1…xn счи-

тать функцией, а какие – аргументами. В качестве функции можно выбрать любую из приведенных переменных, производная по ко-

Приведем ряд полезных для решения задач (а более всего – для умения анализировать предлагаемую задачу и приобретения навы-

ков математического мышления) теорем:

Теорема 3.2 (Ролля). Если функция y = f(x): 1) непрерывна на отрезке [a,b], 2) дифференцируема на интервале (a,b), 3) f(a) = f(b),

то найдется по крайней мере одна точка c (a,b) , в которой f ′(c) = 0 .

Теорема 3.3 (Лагранжа). Если функция y = f(x): 1) непрерывна на отрезке [a,b], 2) дифференцируема на интервале (a,b), то найдется, по крайней мере, одна точка c (a,b) , в которой

1) непрерывны на отрезке [a,b], 2) дифференцируемы на интервале

Использование последней теоремы предполагает сначала анализ производных на указанном в задаче промежутке, а затем в знаменатель выносится та функция, производная которой на этом промежутке не обращается в ноль.

Если мы имеем дело с неявной функцией, задаваемой уравнением f(x1, x2, …, xn) = 0, то сначала анализируются все частные производные функции f(x1, x2, …, xn) в заданной точке и выбирается в качестве неявной функции тот из аргументов x1, x2, …, xn, производная по которому отлична от нуля. Обозначим выбранный таким образом аргумент функции за y. В этом случае все остальные переменные будут являться аргументами этой «избранной» перемен-

33

ной, а производные этой функции по любому аргументу вычисляются по формуле

∂y

Применение этой формулы вполне законно, так как мы на предварительном этапе – выборе одной из переменных x1, x2, …, xn функцией – уже установили отличие стоящей в знаменателе производной от нуля.

Если задана система n уравнений для m > n переменных:

f1 (x1 , x2 ,..., xm )= 0,

..............................

fn (x1 , x2, ..., xm )= 0.

то эта система может определять n неявных функций от n – m аргументов. Для определения тех переменных из нашего набора x1, x2, …, xm, которые могут в данной точке рассматриваться как функции оставшихся переменных, требуется составить матрицу:

∂fn ∂fn ... ∂fn∂x1 ∂x2 xm∂

из всех частных производных наших функций по всем переменным и найти ее ранг. Такая матрица называется функциональной. Номе-

ра столбцов, входящих в ненулевой минор, и определяют те переменные, которые могут быть названы функциями.

Обозначим переменные, которые могут быть выбраны в качестве функций как y1, y2, …, yn, а порядок написания аргументов в функциях f1, f2, …, fn изменим таким образом, чтобы сначала следовали y1, y2, …, yn, а за ними – xn+1, …, xm, которые называются теперь аргументами неявных функций y1, y2, …, yn.

34

Рассмотрим схему построения графика при решении неравенст-

ва.

1. Построение графика y = f (x) начинается с нанесения на бумагу системы координат. Определяется область допустимых значений (ОДЗ) и для наглядности отдельные точки, не входящие в ОДЗ, обозначаются символом ο, а области «сплошных» точек, не входящих в ОДЗ, заштриховываются. Если при стремлении x к точке, помеченной значком ο, функция неограниченно возрастает по мо-

дулю, то через помеченную точку проводят пунктирную вертикальную прямую. Такая прямая называется вертикальной асим-

птотой. Если функция дробно-рациональная, имеющая вид

y(x) = Pn (x) , где Pn (x) и Qn (x) – полиномы степени n и m соответ-

Qm (x)

ственно, то нахождение абсцисс, определяющих вертикальные асимптоты, сводится к решению уравнения Qn (x) = 0. Удобно над значком ο ставить кратность корня этого уравнения, а сам значок мы будем называть «нолик».

Затем находятся корни уравнения Pn (x) = 0 и наносятся на ось абсцисс и отмечаются значком ×, который мы будем называть «крест». Желательно сверху значка × нанести кратность корня (если он определяется).

2. Анализируется поведение функции при x → +∞ и x → −∞ и наносятся на бумагу простейшие «кусочки» линий, отражающие это поведение. Эти «фрагменты» мы будем называть «хвостами» (в школе, кстати, их называли наклонными асимптотами). Если функция не определена при больших по модулю x, то «хвосты» отсутствуют. Если функция определена при каком-то определенном стремлении x к бесконечности, то существует только один «хвост».

Вся предварительная работа закончена, и мы переходим к построению самого графика. Если есть хотя бы один «хвост», то мы продолжаем его в сторону ближайшего «препятствия», т.е. «креста» или «нолика», не пересекая или не касаясь оси абсцисс. В случае «креста» мы обращаем внимание на его кратность. Если кратность «креста» четная, то линия графика только касается оси x, а если нечетная, то пересекает эту ось. Если препятствие – «нолик»,

36

то мы «уводим» нашу линию графика вверх или вниз, взбираясь на вертикальную асимптоту, и продолжаем рисовать график дальше, учитывая кратность «нолика». Если кратность «нолика» нечетная, то мы продолжаем линию, спускаясь (или поднимаясь) с противоположной стороны асимптоты, а если кратность четная, то мы «спускаемся» с той же самой стороны, с какой и взобрались. Рисо-

вание заканчивается, как только мы достигнем противоположного «хвоста».

При построении графика с точки зрения неравенства абсолютно неважна форма кривой – важно лишь контролировать однозначное соответствие y аргументу x и не пересекать или касаться оси x в точках, не помеченных «крестом».

Учтите, это самая общая рекомендация построения графика с точки зрения неравенства. Все возникающие вопросы решайте на

третьем этапе.

Рассмотрим построение графика при исследование функции.

К построенным по предыдущей «инструкции» точкам следует добавить точки, которые мы будем отмечать значком и называть «квадратиком». Эти точки получаются решением уравнения y′(x) = 0. Решив это уравнение и нанеся все «квадратики» на ось x, находим значения функции в этих точках и наносим на бумагу. Эти точки мы также будем обозначать «квадратиками».

Построение графика с «точки зрения исследования функции» отличается от построения графика «с точки зрения неравенства» только тем, что кривая обязательно должна пройти через «квадратики», и на участках от одного препятствия (в число которых теперь входят и построенные «квадратики») до другого она обязана

быть монотонной.

Замечание 1. Может случиться так, что точки, называемые нами «крест» и «нолик», совпадут. Обозначим эту точку как x0. В случае дробно-рациональной функции это означает, что и числитель и знаменатель содержат одинаковые множители в разложении Безу (x – x0), и на этот множитель можно сократить, а для полученной после такого сокращения дробно-рациональной функции вновь начинайте строить график. Если функция не дробно-рациональная,

37

0

то, раскрывая неопределенность 0 , можно получить пределы ис-

ходной функции справа и слева, т.е. значения, к которым должна стремиться кривая графика при x → x0 ± 0 . После построения гра-

фика не забудьте на построенной кривой «выколоть» точку x0. Замечание 2. В том случае, когда функция y (x) не является

дробно-рациональной, для определения кратностей «ноликов» и «крестиков» удобно пользоваться следующей процедурой: для «крестиков» (пусть это будут точки {xk}) брать последовательно производные от функции y(x), вычислять их значения в точках xk. Номер первой по счету производной, отличной от нуля, и будет кратностью рассматриваемого «крестика».

1

Подобная же процедура, только примененная к функции y(x) ,

определяет кратность соответствующих «ноликов», которые для

1

функции y(x) являются уже «крестами».

3.2. Примеры решения задач

Пример 3.1. Требуется выяснить, существует ли первая произ-

Рассмотрим сначала первую точку x = 0. В этой точке функция имеет смысл, является элементарной в окрестности этой точки, а значит, производная существует согласно приведенной в п. 3.1 теории.

В точке x = 1 функция не элементарная, и установление факта существования производной сводится к установлению существования предела

38

Последняя задача относится к гл.2, и мы умеем находить такие пределы. Переходим к реализации всего вышесказанного, т.е. к этапу 4:

т.е. производная существует.

Пример 3.2. Найти производные функции y = ln (x2 – 3x – 4) в точках x = 5 и x = 0.

В точке x = 5 функция существует и элементарна, следовательно, проблемы взятия производной не существует. В точке x = 0 функция по виду также элементарна, но… в этой точке она не определена, и производной также нет.

Для завершения задачи реализуем этап 4:

y′ = (ln(x2 −3x − 4))′ = x2 2−x3−x3−4

и при x = 5 y′ = 76 .

Пример 3.3. Найти производную функции y = xsin x .

Данная функция является сложно-показательной, определена для x > 0, следовательно, производная существует только для таких x. Преобразуем функцию, прологарифмировав ее

ln y = ln(xsin x ) = sin xln x .

Дифференцируем обе части последнего равенства по x:

1y y′ = cos xln x +sin x 1x ,

39

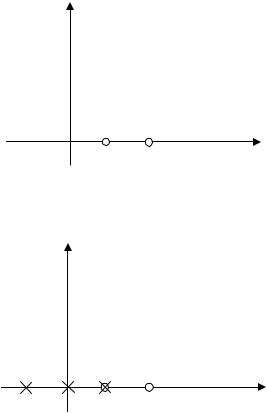
Сначала построим график с точки зрения «неравенства».

1. Наносим точки, в которых функция не определена («ноли-

ки»): x2 + 3x + 2 = 0, x1 = 1, x2 = 2 (рис. 3.1). Римские цифры над

«ноликами» означают кратность соответствующего корня.

y

Рис. 3.1

2. Наносим «кресты»: (x2 – 1)x = 0, x1 = 0, x2 = 1, x3 = – 1 (рис. 3.2).

y

Рис. 3.2

«Крест» совпал с «ноликом». Попытаемся сократить на (x – 1).

«кресты» и вертикальные асимптоты (рис. 3.3).

40