
Башуров Методика решения математических задач 2011
.pdf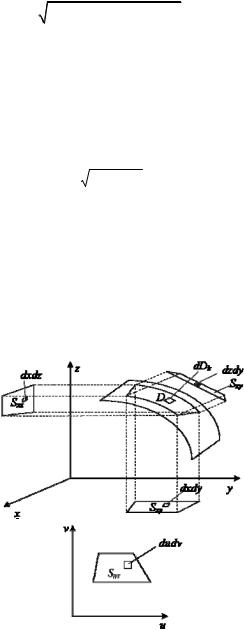
t1
L = ∫ Eϕ′t 2 + 2Fϕ′t ψ′t +Gψ′t 2 dt .
t0
Площадь элементарной площадки, расположенной на поверх-
ности, задаваемой системой
x = ϕ(u,v),
y = ψ(u,v), (8.6)
z = χ(u,v),
вычисляется по формуле
ds = EG − F 2 dudv . |
(8.7) |
Рассмотрим интегралы от функций, заданных на поверхности (поверхностные интегралы).
x = ϕ(u,v),
Пусть на поверхности y = ψ(u,v), задана функция f (x, y, z),
z = χ(u,v),
т.е. функция точек этой поверхности. Рассмотрим область D, являющуюся частью этой поверхности (рис. 8.1, а). На плоскости S(u,v) этому «куску» поверхности отвечает область S (рис. 8.1, б).
а
Рис. 8.1 |
б |
91

Разобьем кусок поверхности D на элементарные площадки dDk, выберем на каждой элементарной площадке произвольную точку Мk(xk,yk,zk) и составим сумму Римана
n |
|
∑ f (xk , yk , zk )dDk . |
(8.8) |
k =1 |
|
Определение 8.1. Предел сумм Римана (8.8) при стремлении площадей всех элементарных площадок к нулю, не зависящий ни от способа разбиения поверхности на элементарные площадки, ни от выбора точек Мk, называется поверхностным интегралом первого рода и имеет обозначение ∫∫ f (x, y, z)ds .
D
Используя выражение для площади элементарной площадки ds =  EG − F 2 dudv , получим выражение для поверхностного инте-
EG − F 2 dudv , получим выражение для поверхностного инте-
грала первого рода ∫∫ f (ϕ(u,v),ψ(u,v),χ(u,v))dudv .
D
Определение 8.2. Если в качестве сомножителей в сумме Ри-
мана (8.8) вместо площадей элементарных площадок dDk брать проекции каждой площадки dxdy, dxdz, dydz (см. рис 8.1, а) на ко-
ординатные плоскости (а таковых в нашем пространстве три), то получатся три поверхностных интеграла второго рода:
∫∫ f (x, y, z)dxdy , |
∫∫ f (x, y, z)dxdz |
и ∫∫ f (x, y, z)dydz . |
D |
D |
D |
Часто вместо трех интегралов рассматривают одновременно все
∫∫P(x, y, z)dydz +Q(x, y, z)dxdz + R(x, y, z)dxdy ,
D
где функции P(x,y,z), Q(x,y,z) и R(x,y,z) определены на одной по-
x = ϕ(u,v),
верхности, заданной системой y = ψ(u,v),
z = χ(u,v).
Для взятия интеграла второго рода надо определиться, в какую сторону направлять нормаль к поверхности, так как от этого выбора зависит не величина косинусов, а их знак. Зачастую различают внешнюю и внутреннюю стороны поверхности и нормали, которые
92

соответственно называются внешней и внутренней. Стороны поверхности отличаются тем, что при попытке перейти с одной стороны на другую направление нормали меняется скачком на противоположное. Поверхности, для которых нельзя различить внешнюю и внутреннюю стороны, называются односторонними (приме-
ром такой поверхности является «лист Мебиуса», изображенный на рис. 8.2).
При путешествии по поверхности Мебиуса можно выбрать такой маршрут, двигаясь по которому и следя за направлением нормали, обнаруживается, что вернувшись в исходную точку, наш перпендикуляр к поверхности направлен в противоположную сторону от своего первоначального положения. При этом никаких резких изменений (скачков) перпендикуляр не испытывал.
Свойства этих интегралов аналогичны свойствам тегралов (двойных, криволинейных и т.д.).
Рис. 8.2
прежних ин-
Интеграл первого рода сводится к двойному интегралу по области S в плоскости (u,v) путем формальной подстановки в инте-
грал ∫∫ f (x, y, z)ds выражения площади элементарной площадки
D
через коэффициенты первой квадратичной формы Гаусса
|
ds = EG − F 2 dudv , |
(8.9) |
∫∫ f (x, y, z)ds = ∫∫ f (ϕ(u,v),ψ(u,v)χ(u,v)) |
EG − F 2 dudv . |
|
D |
S |
|
Интегралы второго рода вычисляются либо сведением искомого интеграла второго рода к первому при помощи формул dxdy = ds cos(N, k ) , dydz = ds cos(N,i ) , dxdz = ds cos(N, j) , либо,
что самое удобное, записью уравнения поверхности в виде z = z(x,y). Тогда получим, например,
∫∫R(x, y, z)dxdy = ∫∫R(x, y, z (x, y))dxdy .
D S
Определение 8.3. Если в области D пространства нескольких переменных (x1, …, xn), являющимися декартовыми координатами,
93
задана функция U (x1, …, xn), то говорят, что в области D задано
скалярное поле функции U.
Определение 8.4. Если в области D пространства нескольких переменных задана векторная функция a(x1, ..., xn ) , то говорят, что
вобласти D задано векторное поле a .
Втом случае, когда речь идет о трехмерном пространстве, то используются обозначения для координат x, y, z, а для ортов репе-
ра – i , j, k .
Определение 8.5. В области D , на которой задано скалярное
поле функции U (x1, …, xn), может быть определен дифференциальный оператор, называемый градиентом функции U (x1, …, xn) и
обозначаемый либо
n |
|
∂U |
|
|
||
grad U = ∑ |
ek , |
(8.10) |
||||
|
|
|||||
1 |
|
∂x |
|
|||
либо |
|
|
|
|
|
|
n |
∂U |
|
|
|
||
U = ∑ |
ek . |
(8.11) |
||||
|
||||||
1 |
∂x |
|
||||
Этот дифференциальный оператор ставит в соответствие скалярному полю U векторное поле grad U.
n
Определение 8.6. Дивергенцией векторного поля a = ∑ak ek
называется скаляр |
|
|
1 |
|
|
|
|
||
n |
∂ak |
|
|
|
div a = ∑ |
. |
(8.12) |
||
|
||||
1 |
∂xk |
|
||
Этот дифференциальный оператор ставит в соответствие векторному полю a скалярное поле div a .
Определение 8.7. Ротором векторного поля a называется век-
торное поле, обозначаемое |
rot a |
и определяемое в |
трехмерном |
||||||
пространстве равенством |
|
|
|
|
|
|
|
|
|
|
|
i |
|
j |
|
k |
|
|
|
|
|
|
|
|
|
||||
rot a = |
|
∂ |
|
∂ |
|
∂ |
|
. |
(8.13) |
∂x |
|
∂y |
∂z |
||||||
|
|
|
|
|
|||||
|
ax |
|
ay |
|
az |
|
|
||
94
Этот дифференциальный оператор ставит в соответствие векторному полю a также векторное поле rot a . Такие выражения
имеют дифференциальные операторы в декартовых координатах. В том случае, когда пространство задается не декартовыми ко-
ординатами, а какими-либо другими, выражения для перечисленных выше операторов меняют свой вид, и для конкретных систем координат их можно найти в справочнике [4]. Если мы проследим
за изменением функции u (x1, …, xn), определяющей скалярное поле u, следуя вдоль кривой Г, заданной уравнениями (8.1), или, что то
же самое, одним векторным уравнением r = r (t) , то приращение функции u (x1, …, xn), или скорость ее изменения, определяется «производной по направлению»
∂u |
n |
∂u |
|
|
|
= ∑ |
Ak , |
(8.14) |
|||
∂e |
∂x |
||||
|
1 |
k |
|
||
где Ak – косинусы углов, образованных единичным вектором касательной r0 к кривой Г с осями координат. Производную по направлению часто удобно использовать в виде
∂u |
= (grad u, τ ) . |
(8.15) |
|
||
∂e |
0 |
|
|
|
Из этого выражения для производной по направлению следует, что направление наибольшего роста функции совпадает с направлением градиента этой функции. В любом другом направлении функция растет медленнее.
Интегрируя векторное поле a по какому-либо замкнутому кон-
туру Г, получим выражение для «циркуляции вектора a |
по конту- |
ру Г » |
|
n |
|
cirk a = ∫∑ak dxk . |
(8.16) |
Г 1 |
|
Последнее выражение можно использовать в векторной форме |
|
cirk a = ∫(a ds) , |
(8.17) |
Г |
|
где ds – вектор с координатами (dx1, …, dxn).
Если нам заданы замкнутый контур Г и векторное поле a , то можно рассмотреть поверхность S, «опирающуюся» на контур Г (рис. 8.3) и рассмотреть выражение
95
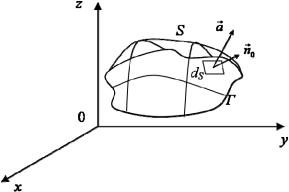
∫∫(a, n0 )ds . (8.18)
S
Рис. 8.3
Этот интеграл носит название «поток вектора a через поверхность S». В этом интеграле вектор n0 является вектором единичной нормали к поверхности и в случае задания поверхности неявной функцией ϕ(x1, …, xn) = 0 может быть выражен при помощи градиента этой функции
n |
= |
ϕ |
. |
(8.19) |
|
ϕ |
|||||
0 |
|
|
|
||
Формула Стокса связывает циркуляцию вектора a |
по замкну- |
||||
тому контуру Г с его потоком через поверхность S, опирающуюся |
|||||
на контур Г (см. рис. 8.3): |
|
|
|
|
|
cirk a = ∫(a ds) = ∫∫(a n0 )ds . |
(8.20) |
||||
ГS
Если нам задана замкнутая поверхность S и вектор n0 является вектором единичной внешней нормали к этой поверхности, а вектор a(x, y, z) образует векторное поле, то справедлива формула,
часто называемая формулой Гаусса–Остроградского:
∫∫(a ds)ds = ∫∫∫div a dv . |
(8.21) |
|
S |
V |
|
Здесь V – объем, ограниченный поверхностью S.
96

8.2. Примеры решения задач
Пример 8.1. Построить трехгранник Френе для кривой, заданной в векторной форме r (t) = sin t i + cost j +t k .
Выразим сначала уравнение кривой в виде r (s) , где s – нату-
ральный параметр, выражаемый интегралом (8.3). Для нашей кривой интеграл удается взять и связь между параметром s и парамет-
ром t можно записать в виде t = |
|
|
s |
|
. А само уравнение кривой в |
||||||||||||||||||||||||||||||||||||||
2 |
|||||||||||||||||||||||||||||||||||||||||||
виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
s |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
r (s) = sin |
|
i + cos |
|
|
j + |
|
|
k . |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Тогда первое уравнение из системы Френе дает первый вектор |
|||||||||||||||||||||||||||||||||||||||||||
трехгранника |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
τ0 = |
dr |
= |
|
1 |
|
cos |
|
s |
i |
− |
1 |
|
|
sin |
|
s |
|
j + |
1 |
|
k . |
|
|
|
||||||||||||||||
ds |
2 |
|
2 |
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||||||
Второе уравнение позволяет сразу найти второй |
вектор |
n0 , |
|||||||||||||||||||||||||||||||||||||||||
правда, для этого потребуется разделить производную вектора |
d τ0 |
|
|||||||||||||||||||||||||||||||||||||||||
ds |
|||||||||||||||||||||||||||||||||||||||||||
на ее модуль: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
d τ0 |
= − |
|
1 |
sin |
s |
|
|
i − |
1 |
|
cos |
|
|
s |
j , |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
2 |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
ds |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
d τ0 |
|
= k = |
|
1 |
|
|
и |
|
n |
= − |
1 |
|
|
|
sin |
s |
|
i + cos |
s |
j . |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
ds |
|
|
|
2 |
|
|
|
0 |
|
|
|
2 2 |
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Обратимся к третьему уравнению системы Френе: dn0
ds
откуда
æb0 = dnds0 + kτ0 =
=− 14 (cos s2 i −sin s2 j) + 12 ( 12 cos s2 i − 12 sin s2 j + 12 k ) =
97
= |
1 |
cos |
s |
i − |
1 |
sin |
s |
j + |
1 |
k . |
|
4 |
2 |
4 |
2 |
2 |
|||||||
|
|
|
|
|
|
Из последней формулы найдем кручение, при условии, что длина вектора b0 =1:
|
1 |
|
|
2 |
|
s |
|
|
2 |
|
s |
1 |
|
5 |
|
|||||||||
æ = |
|
|
|
cos |
|
|
|
+sin |
|
|
|
|
+ |
|
|
= |
|
|
|
|
||||
16 |
|
|
2 |
|
|
2 |
|
4 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|||||||||||
и вектор |
1 |
|
|
|
s |
|
|
1 |
|
|
|
|
s |
|
|
2 |
|
|
||||||
b = |
|
cos |
|
i − |
sin |
|
j + |
k . |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
0 |
5 |
|
|
|
2 |
|
|
5 |
|
|
|
2 |
|
|
|
|
5 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Все три орта трехгранника найдены.
Пример 8.2. Найти кривизну кривой в точке t = 0. Кривая за-
x = t −1,
дана системой y = t2 ,
z = sin t.
Сначала совершим переход к естественным координатам по формуле (8.3):
t |
t |
s = ∫ |
x′2 (t )+ y′2 (t )+ z′2 (t )dt = ∫ 1+ 4t2 + cos2 tdt . |
0 |
0 |
Обратим внимание на то, что интеграл «не берущийся». Однако нам нет необходимости его брать, чтобы найти функциональную зависимость t от s. В формулах Френе присутствуют лишь производные от векторов, а производные можно определить и без нахождения функциональной зависимости. Надо только помнить, что
d |
= |
d dt |
= |
d |
1 |
. |
|||
|
|
|
|
|
|
|
|||
ds |
dt ds |
dt |
|
1+ 4t2 + cos2 t |
|||||
|
|
|
|
||||||
Поскольку кривая в векторном виде задана уравнением r (t) = (t −1)i +t2 j +sin t k ,
то в точке t = 0
τ0 |
= |
dr |
|
dt |
= (−i + 2t j + cost k ) |
1 |
|
|
|
= − |
1 |
i + |
1 |
k . |
dt |
|
ds |
1+ 4t2 + cos2 t |
|
t =0 |
2 |
2 |
|||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
98 |
|
|
|
|
|
|
|
|

В свою очередь,
kn0 = |
dτ |
0 |
|
= |
d |
(−i + 2t j + cost k ) |
|
1 |
|
|
|
|
1 |
|
|
|
= |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
2 |
|
2 |
|
|
2 |
|
|
2 |
|
|||||||||
|
ds |
|
|
|
|
|
|
|
1+ 4t |
+ cos |
|
|
1+ 4t |
+ cos |
t |
||||||||
|
|
|
dt |
|
|
|
|
|
t |
|
|
||||||||||||
|
|
= |
|
|
2 j −sin t k |
+ |
(−i + 2t |
j +cost k )(−4t +sin t cost) |
. |
|
|
|
|||||||||||
|
|
1+ 4t2 +cos2 t |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
(1+ 4t2 +cos2 t)2 |
|
|
|
|
|
|
|
||||||||||
Получим выражение для второго вектора в трехграннике Френе kn0 = j , где k – кривизна кривой в точке t = 0. Так как оба вектора
τ0 и n0 единичной длины, то k = 1.
Пример 8.3. Вычислить поверхностный интеграл
∫∫(x2 + y2 + z2 )2 ds ,
S
где S – первый октант сферы радиуса R = 2 с центром в точке (0,0,0). Уравнение такой сферы имеет вид x2 + y2 + z2 = 4 . Найдем вы-
ражение для элементарной площади dS. Для этого сначала определим коэффициенты первой квадратичной формы Гаусса, предварительно перейдя к сферическим координатам (они выполняют роль криволинейных координат):
x = 2cos ϕcos ψ,y = 2cos ϕsin ψ, .z = 2sin ϕ,
Е = 4, F = 0, G = 4cos2ϕ.
Воспользуемся формулой (8.9) и получим требуемое выражение ds = 4cosϕdϕdψ. Поскольку параметры ϕ и ψ (широта и долго-
|
|
π |
|
та) меняются в промежутке |
0, |
|
, а |
|
|||
|
|
2 |
|
подынтегральная |
функция |
||
f (x, y, z) = (x2 + y2 + z2 )2 =16 , то ин- |
|||
теграл превращается в обыкновенный |
|||
двойной интеграл ∫∫64cos ϕdϕdψ по
D |
|
области, изображенной на рис. 8.4. |
Рис. 8.4 |
99

Взять такой интеграл по данной области не представляет труда
|
π |
|
|
||
|
2 |
|
π |
|
|
∫∫64cosϕdϕdψ = 64∫cos ϕ |
dϕ = 32π . |
||||
2 |
|||||
D |
0 |
|
|
||
Пример 8.4. Требуется составить первую квадратичную форму Гаусса для эллипсоида
x2 |
+ |
y2 |
+ z2 =1. |
(8.22) |
9 |
|
|||
16 |
|
|
||
Поскольку в нашем «справочном бюро» (п. 8.1) все коэффициенты выражаются исходя из параметрического представления поверхности, выберем в качестве таковых переменные y и z:
y = u, z = v, |
x = 1− u2 |
−v2 . |
|
16 |
|
Однако такое представление неудобно тем, что придется дифференцировать квадратные корни (хотя абсолютно правомерно). Поэтому воспользуемся представлением эллипсоидальной поверхности в эллиптической системе координат:
x = 3rcosϕcosψ, y = 4rcosϕsinψ, z = rsinϕ,
а уравнение эллипсоида записывается в виде r = 1.
В том, что это уравнение задает наш эллипсоид, легко убедиться, подставив в уравнение (8.22) выражения координат x, y и z через параметры ϕ и ψ.
Сами коэффициенты находятся при помощи формул (8.4):
E = sin2ϕ(9cos2ψ + 16sin2ψ) + cos2ϕ, G = cos2ϕ(9sin2ψ + 16cos2ψ),
F= 3sin(ϕ + ψ) + 4cos(ϕ + ψ),
аквадратичная форма, вычисляемая по формуле (8.5) имеет вид:
(sin2ϕ(9cos2ψ + 16sin2ψ) + cos2ϕ)dϕ2 +
+(6sin(ϕ + ψ) + 8cos(ϕ + ψ)) dϕ dψ +
+cos2ϕ(9sin2ψ + 16cos2ψ)dψ2.
100
