дискретка_все_практики / дискретка / Razdel_3_Praktika_5

Раздел 3. Основы комбинаторики

ПРАКТИЧЕСКАЯ РАБОТА № 5

ЭЛЕМЕНТЫ КОМБИНАТОРИКИ

1. ОБЩИЕ СВЕДЕНИЯ

Комбинаторика – область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.

Теперь дадим определения основным терминам комбинаторики.

Произвольное к-элементное подмножество п-элементного множества называется сочетанием из п элементов по к.

Теорема.

Число всех к-элементных подмножеств из п элементов

равно

Доказательство.

Обозначим

Чтобы построить к-элементное подмножество множество А, нужно к (к-1)-элементному подмножеству присоединить один из (n-к+1) элементов, которые не входят в это подмножество.

Поскольку (к-1)-элементных подмножеств имеется

И каждый из них можно сделать к-элементным (n-к+1) способами, то таким образом мы получим подмножеств.

Но не все они будут разными, так каждое к-элементное множество можно так построить к способами: присоединением каждого из к его элементов. Поэтому вычисленное нами число в к раз больше, чем число

к-элементных подмножеств. Следовательно,

О тсюда найдем

Но число одноэлементных подмножеств множества А равно количеству элементов, то есть n. Подставив вместо

число n, получим (1).

Таким образом мы установили, что число сочетаний из n элементов по к равно

Множество называется упорядоченным, если каждому элементу этого множества поставлено в соответствие некоторое число (номер элемента) от 1 до n, где n – число элементов множества, так что различным элементам соответствуют различные числа. Всякое конечное множество можно сделать упорядоченным, если, например, переписать все элементы множества в некоторый список (а,в,с…), а затем поставить в соответствие каждому элементу номер места, на котором он стоит в списке.

Различные упорядоченные множества, которые отличаются лишь порядком элементов (то есть могут быть получены из того же самого множества), называются перестановками этого множества.

Теорема.

Число перестановок в множестве рассчитывается по формуле:

Доказательство.

Будем последовательно выбирать элементы множества А и размещать их в определенном порядке на n местах. На первое место можно поставить любой из n элементов. После того, как заполнено первое место, на второе место можно поставить любой из оставшихся (n-1) элементов и т.д. По правилу умножения все n мест можно заполнить

способами.

Следовательно, множество А из n элементов можно упорядочить n! способами.

Рассмотрим теперь упорядоченное подмножество данного множества А. Само множество А считается неупорядоченным, поэтому каждое его подмножество может быть упорядочено каким-либо возможным способом. Число всех к-элементных подмножеств в множестве А равно

Каждое такое подмножество можно упорядочить к! способами. Таким образом получим все упорядоченные к-элементные подмножества множества А. Следовательно, их число будет

Теорема.

Число упорядоченных к-элементных подмножеств множества, состоящего из n элементов равно

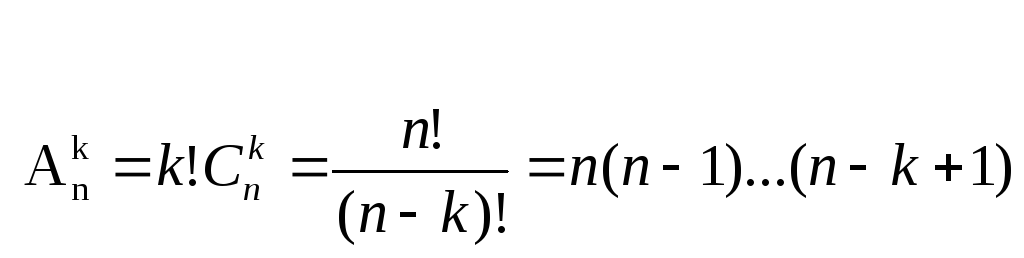
Упорядоченные к-элементные подмножества множества из n элементов называются размещениями из n элементов по к . Различные размещения из n элементов по к отличаются количеством элементов либо их порядком.

Следовательно число различных размещений из n по к равно

Сочетаниями из n элементов по к с повторениями называются группы, содержащие n элементов, причем каждый элемент принадлежит к одному из m типов.

Теорема.

Число различных сочетаний из m элементов по n с повторениями равно

Доказательство.

Каждое сочетание полностью определяется, если указать, сколько элементов каждого типа в него входит. Поставим в соответствие каждому сочетанию последовательность нулей и единиц, составленную по такому правилу: напишем подряд столько единиц, сколько элементов первого типа входит в сочетание, далее поставим нуль и после него напишем столько единиц, сколько элементов второго типа содержит это сочетание и т. д.

Например: из трех элементов a, b, c можно составить такие сочетания по два с повторениями:

aa ac bc ab bc cc

Написанным сочетаниям из трех букв по две будут соответствовать такие последовательности:

1100, 1001, 0101, 0110, 0011.

Таким образом, каждому сочетанию из m элементов по n соответствует последовательность из n единиц и m-1 нулей, и равно наоборот,

по каждой такой последовательности однозначно восстанавливается такое сочетание. Поэтому число сочетаний из m по n с повторениями равно числу последовательностей из n единиц и m-1 нулей, т.е.

Перестановки с повторениями.

Пусть имеется n элементов. Из них можно составить к групп так, что в одну группу входят тождественные между собой элементы, а группы различимы между собой. Число элементов обозначим к1, к2, …, кn такое, что к1+к2+…+кn=n.

Перестановкой из n элементов с повторениями называется такая совокупность, в которую входит n элементов, расположенных в каком-либо порядке.

Теорема.

Число различных перестановок, которые можно составить из n элементов, среди которых имеется k1 элементов первого типа, k2 элементов второго типа,…, k3 элементов m-го типа, равно

Доказательство.

Рассмотрим одну перестановку и заменим в ней все элементы разными. Тогда число различных перестановок, которые можно составить из рассматриваемой нами перестановки, равно

k1!k2!…k3!. Проделав это для каждой перестановки, получим n! перестановок. Следовательно, размещением из n элементов по к с повторением называется такая совокупность, которая содержит к элементов, записанных в каком-либо порядке из данных m различных между собой элементов, причем один и тот же элемент может входить в совокупность несколько раз.

Число размещений можно рассчитать по формуле:

2. ЦЕЛЬ И ПОРЯДОК РАБОТЫ

Цель работы—получить начальные сведения об элементах комбинаторики, научиться выполнять элементарные расчеты с использованием элементов комбинаторики, знать основные определения и формулы комбинаторики.

Работу следует выполнять в следующем порядке:

• изучить описание работы;

• согласно своему варианту задания, решить заданные примеры без применения ЭВМ;

• разработать алгоритмы решения отдельных задач и оформить в виде процедур;

• разработать и отладить программу в соответствии с заданием;

• решить задачу с помощью программы и записать результат для одного из случаев генерации;

• оформить отчет.

3. ЗАДАНИЯ

3.1 Согласно своему варианту получить результат вычислений перестановок, сочетаний и размещений.

2. Разработать процедуры вычисления перестановок, сочетаний, размещений, а также перестановок, размещений и сочетаний с повторениями.

3. Разработать программу на основе разработанных процедур, выполняющую вычисления согласно варианту, отладить и протестировать ее.

4. ЗАДАНИЯ ДЛЯ РУЧНОГО ПРОСЧЕТА

1. Сколькими способами можно выбрать 6 одинаковых или разных пирожных в кондитерской, где есть 11 разных сортов пирожных?

2. Имеется 7 бусинок. Сколько различных ожерелий можно составить из этих семи бусинок?

3. Учащимся необходимо сдать 4 экзамена на протяжении 8 дней. Сколькими способами это можно сделать?

4. Научное общество состоит из 25 человек. Надо выбрать президента общества, вице-президента , ученого секретаря и казначея. Сколькими способами может быть сделан этот выбор, если каждый член общества может занимать лишь один пост?

5. 10 кресел поставлены в ряд. Сколькими способами в них могут сесть 2 человека? Сколько способов сесть рядом? Сколько способов сесть через кресло?

6. Имеется 5 юношей и 5 девушек. Сколько существует способов рассадить их так, чтобы два лица одного пола не сидели вместе (за круглым столом)?

7. Сколько можно составить перестановок из 10 элементов, в которых данные 2 элемента не стоят рядом?

8. 7 девушек водят хоровод. Сколькими различными способами они могут стать в хоровод?

9. В классе 30 одноместных парт. Сколькими способами на них можно посадить 6 студентов специальности 22.04?

10. Сколько пятизначных чисел можно составить из цифр 1,2,4,6,7,8, если ни одну цифру не использовать более одного раза.

11. Укротитель хищников выводит на арену 5 львов и 4 тигра. 2 тигра не должны идти друг за другом. Сколькими способами можно расставить зверей.

12. Сколькими способами 8 человек могут стать в очередь к театральной кассе?

13. В кондитерском магазине продавалось четыре сорта пирожных: “наполеоны”, “эклеры”, “песочные” и “слоеные”. Сколькими способами можно купить 7 пирожных?

14. В комнате 9 лампочек. Сколько всего разных способов освещения комнаты, при которых горит ровно три лампочки ?

15. Сколькими способами можно разделить 15 предметов на три группы так, чтобы в одной группе было 4 предмета, в другой – 8, в третьей – 3.

5. ЗАДАНИЯ ДЛЯ РЕШЕНИЯ НА КОМПЬЮТЕРЕ

1. Сколькими способами может построиться в шеренгу группа гимнастов из 5-ти человек?

2. Сколькими способами могут сесть в лодку 5 человек , если на веслах могут сидеть только двое?

3. Сколько 5-тизначных чисел можно составить из цифр 1,2,4,6,7,8, если никакую цифру не использовать больше одного раза?

4. Сколько 3-хзначных чисел можно составить из цифр 3,2,1,0,1,8?

5. В классе 30 одноместных парт. Сколькими способами за них могут сесть 6 человек?

6. В парке на карусели свободно 20 мест. Сколькими способами на них могут сесть 8 человек?

7. Сколькими способами из 8-ми человек можно создать комиссию из 5-ти человек?

8. Сколькими способами мама может разделить между тремя детьми 12 различных конфет.

9. На Новый год Пятачок решил подарить Пуху и ослику Иа по шарику. Всего у него 7 шариков. Сколькими способами он может выбрать эти 2 шарика?

10. Сколькими способами из 6 фигурок можно составить пары (по две фигурки).

11. На книжной полке стоят 12 книг. Сколькими способами можно выбрать из них 5 книг так, чтобы никакие две из них не стояли рядом? )

12. Имеется 5 юношей и 5 девушек. Сколько существует способов рассадить их так, чтобы два лица одного пола не сидели вместе (за круглым столом)?

13. Научное общество состоит из 25 человек. Надо выбрать президента общества, вице-президента , ученого секретаря и казначея. Сколькими способами может быть сделан этот выбор, если каждый член общества может занимать лишь один пост?

14. Имеется 7 юношей и 4 девушки. Выбрать 6 человек так, чтобы среди них было не менее 2х девушек. Сколькими способами это можно сделать?

15. Сколько имеется четырехзначных чисел, у которых

каждая последующая цифра больше предыдущей?

6. МЕТОДИЧЕСКИЕ УКАЗАНИЯ

В данных методических указаниях вам будут предложены некоторые стандартные процедуры генерации перестановок, сочетаний и повторений, а также стандартная рекурсивная функция для вычисления факториала, чтобы облегчить пересчет перестановок, сочетаний и размещений с повторениями.

Процедура генерации размещения:

procedure razmeshenie;

begin

r:=1;

for i:=1 to m-k do

begin

A:=r*i;

r:=A

end;

begin

t:=1;

for i:=1 to m do

begin

B:=t*i;

t:=B

end

end;

Ta:=B/A

end;

Процедура генерации перестановок:

procedure perestanovki;

begin

x:=1;

for i:=1 to n do

begin

D:=x*i;

x:=D

end

end;

Процедура генерации сочетаний:

procedure sochet;

begin

soch:=1;

for i:=1 to m_1-k_1 do

begin

C:=soch*i;

soch:=C

end;

begin

z:=1;

for i:=1 to m_1 do

begin

S:=z*i;

z:=S

end

end;

begin

so:=1;

for i:=1 to k_1 do

begin

q:=so*i

so:=q

end

end;

Tap:=S/(C*q);

end;

Стандартная функция вычисления значения факториала числа:

Function Factorial (i:integer):LongInt;

Begin

If i <> 0 then

Factorial:=i*Factorial(i-1);

Else Factorial:=1;

End.

7. СОДЕРЖАНИЕ ОТЧЕТА

Отчет должен содержать:

• наименование работы, постановку задачи

• выбранный вариант задания

• результаты решения всех задач без применения ЭВМ

• программу решения задачи(представляется в электронном виде)

• результаты работы всех разделов программы и их анализ.

8. КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Дайте определение понятию “комбинаторика”.

2. Что называют перестановкой из k элементов?

3. Что такое сочетание из n элементов по k?

4. Что называют размещением из n элементов по k ?

5. Что называют перестановкой из k элементов с повторениями?

6.Что такое сочетание из n элементов по k с повторениями?

7. Что называют размещением из n элементов по k с повторениями?

9. ИСПОЛЬЗУЕМАЯ ЛИТЕРАТУРА

1. В. Липский. Комбинаторика для программистов. М. “Мир”, 1988.

2. Алгоритмические исследования в комбинаторике. (Под ред. Фараджева И. А.) М., Наука, 1978.

3. Ежов И.И., Скороход А.В., Ядренко М.И. Элементы комбинаторики. М., Наука, 1988.-208с.

4. Виленкин Н.Я. Комбинаторика. М.,1978.-170с.

9