
отвкты на математику
.pdf
направляющим вектором прямой. Составим |
|
уравнение |
прямой |
по |
точке |
M 0 и |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
направляющему вектору M 0 M1 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
x x0 |
|
y y0 |
|
|
|
z z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
x |
x |
0 |
|
|
|
y y |
0 |
|
|
|
z z |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
35. Прямая по точке перпендикулярно плоскости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть необходимо составить уравнение прямой , |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
проходящей |
|
|
через |
точку |
М 0 (х0 , у0 , z0 ) , |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
перпендикулярно |
|
|
плоскости |
|
, |
заданной |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
уравнением: Ах+Ву+Сz+D=0. Выпишем нормаль к |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
плоскости, |
вектор |
|
n ( A, B,C) . |
Для |
искомой |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
прямой этот вектор является направляющим |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вектором. Составим уравнение прямой |
по точке |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
М 0 и направляющему вектору n : |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
x x0 |
|
|
y y0 |
|
|
z z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
A |
|
|
|
B |
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
36. Перевод прямой из общего в канонический вид, |
из канонического в общий. |
|
|
|
|
||||||||||||||||||||||||||||
Пусть прямая задана в |
|
|
|
|
|
|
|
|
|
|
A x B y C z D 0 |
|
|
|
|
||||||||||||||||||
|
общем |
виде: |
|
1 |
1 |
1 |
1 |
|
|
для того, |
чтобы |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 x B2 y C2 z D2 0 |
|
|
|
|
||||||||||||
перевести ее в канонический вид, возьмем две точки принадлежащие данной прямой, т.е. два частных решения данной системы. Для получения частного решения системы, проще всего одной
из переменных дать произвольное значение, например, |
|
|
х0 |
0 . Подставить это значение в систему |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B y C z |
D |
|
|
|
|
|
|
|
|
|
||||
и решить полученную систему с двумя переменными: 1 |
1 |
1 , например, по правилу |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B2 y C2 z |
D2 |
|
|
|
|
|
|
|
|
|
||||
Крамера: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
D1 |
|
C1 |
|
|
|
|
|
|
|
|
|
B1 |
D1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
y |
0 |
|
1 |
|
|
|
|
D2 |
|
C2 |
|
|
, z |
0 |
|
2 |
|
|
|
B2 |
D2 |
|
|
, найдена точка М |
0 |
(х |
0 |
, у |
0 |
, z |
0 |
) |
. Если же |
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
B1 |
C1 |
|
|
|
|
|
|
|
C1 |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
B1 |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B2 |
C2 |
|
|
|
|
|
|
|
|
|
B2 |
C2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
определитель |
|
|
B1 |
C1 |
|
0 , то необходимо другой переменной дать произвольное значение, |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
B2 |
C2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
например, |
y0 0 и решить систему относительно х и z .Аналогично найти еще одно частное |
||||||||||||||||||||||||||||||||||||||||||||||
решение |
|
системы |
|
M1 (x1 , y1 , z1 ) . |
И |
записать |
|
уравнение |
прямой |
|
по |
двум |
точкам: |
||||||||||||||||||||||||||||||||||
|
x x0 |
|
y y0 |
|
|
z z0 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
y y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
x |
x |
0 |
|
|
0 |
|
|
|
|
|
z z |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Перевод уравнения прямой из канонического вида в общий

Пусть дана прямая |
в каноническом виде: |
х х0 |
|
y y0 |
|
z z0 |
. Для того, |
чтобы ее |
|
m |
|
p |
|||||||
|
|
|
|
n |
|
|
|
||
перевести в общий вид, |
приравняем попарно |
отношения |
( |
при условии, что |
n 0 ): |
||||
x x0 |
|||
|
|
|
|
m |
|
||
y y |
|
||
|
|
0 |
|
|
|
|
|
|
n |
|
|
|
|
||
|
|
y y0 |
n(x x0 ) m( y y0 ) |
0 |
|
|
n |
||||
|
|
||||
|
|
z z0 |
|
после преобразований получим: |
|
|
|
p( y y0 ) n(z z0 ) |
0 |
||
|
p |
||||
|
|
|
|
||
Прямая получена в общем виде, как пересечение двух плоскостей. Если же n=0. то можно получить одну из плоскостей, приравняв первое отношение к третьему.
37. Предел числовой последовательности, предел функции в точке, односторонние пределы.
Определение 1: Число a называется пределом последовательности , если для любого сколь угодно малого положительного числа найдется такое натуральное число N, зависящее от , что при всех п > N выполняется неравенство
xn a .
Определение 1 ( «на языке − », или по Коши): |
|
|
|
|
|
|
|
|
|
||||
Число А называется пределом функции f x при x a , если для любого числа |
0 можно |
||||||||||||
указать такое 0 , |
что для любого х, |
удовлетворяющего |
неравенству |
0 |
|
x a |
|
, |
|||||
|
|
||||||||||||
|
|
||||||||||||
|
|
f x A |
|
. В этом случае пишут |
lim f x A |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||
выполняется неравенство |
|
|
x a |
. |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||||
Определение 2 ( «на языке последовательностей», или по Гейне ): |
|
|
|
|
|
|
|
|
|||||
Число А называется пределом функции f(x) |
в точке a (или при x a ), |
если для любой |
|||||||||||
последовательности допустимых значений аргумента , сходящейся к a, (т.е. |
lim |
→∞ |
= ), |
||||||||||
|
|
|
|
|
|
|
|
|
|||||
последовательность соответствующих значений функции сходится к числу А(т.е. lim |
= |
||||||||||||
|
|
|
|
|
|
|
|
→∞ |
|
|
|
||
).
Заметим, что для существования предела функции в точке a вовсе не требуется, чтобы функция f x была непременно определена в точке a. Для того чтобы функция f x стремилась к
пределу при x a , необходимо лишь, чтобы в области еѐ определения были точки, как угодно близкие к a и отличные от a.
Односторонние пределы:
Если число A1 есть предел функции y f x при х стремящемся к а так, что х принимает
только значения, меньшие а, то A1 называется левым пределом функции f x в точке а:
lim f x A1 ,
x a 0
Если число A2 есть предел функции y f x при х стремящемся к а так, что х принимает
только значения, большие а, A2 называется правым пределом функции f x в точке а:
lim f x A2 .
x a 0
33. правило вычисления пределов.
Примеры
Пример 1. Вычислить lim 5x3 6x2 x 5 .
x 2
Решение. По правилу нахождения предела многочлена находим
lim 5x3 6x 2 |
x 5 5 23 6 22 |
2 5 13. |
|||||||||
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
lim |
x 2 x 1 |
|
|
|
|
|||||
Пример 2: Вычислить |
|
|
|
. |
|
|
|
|
|
||
|
|
|
|
|
|
|
|||||
|
x 2 |
x 3 |
|
|
|
|
|||||
Решение. Так как при x 2 знаменатель дроби отличен от нуля, то по правилу нахождения |
|||||||||||
предела дробно-рациональной функции получим |
|
|
|
||||||||
|
|
|
lim |
x 2 x 1 |
|
22 2 1 |
3. |
||||
|
|
|
|
x 3 |
|
2 3 |
|
||||
|
|
|
x 2 |
|
|
|
|||||
Пример 3: Вычислить |
lim |
|
5 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
x 2 |
4x 8 |
|
|
|
|
|||||
Решение. Предел делителя равен нулю: |
lim 4x 8 4 2 8 0. Следовательно, |
теорему |
|||||||||||||
|
|
|
|
|
|
|
x 2 |
|
|
|
|
|
|
||
о пределе применять нельзя. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Так как lim 4x 8 0, то |
4x 8 |
при |
x 2 есть бесконечно малая, |
а обратная ей |
|||||||||||
|
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
— бесконечно большая. Поэтому при x 2 |
|
|
1 |
|
5 есть |
|||||||||
величина |
|
произведение |
|
|
|||||||||||
4x 8 |
4x 8 |
||||||||||||||
величина бесконечно большая, т.е. |
lim |
|
5 |
|
. |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||
4x |
|
8 |
|
|
|
|
|
||||||||
|
|
|
|
x 2 |
|
|
|
|
|
|
|
||||
Пример 4: Вычислить lim |
3x 2 |
2x |
. |
|
|
|
|
|
|
|
|
|
|||
2x 2 |
5x |
|
|
|
|
|
|
|
|
|
|||||
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|||
Решение. Здесь пределы |
числителя |
|
и |
знаменателя |
при x 0 |
равны |
нулю. |
||||||||
Непосредственной подстановкой вместо аргумента его предельного значения вычислить предел
нельзя, так как при x 0 получается отношение двух бесконечно малых величин.
Разложим числитель и знаменатель на множители, чтобы сократить дробь на общий множитель, стремящийся к нулю, и следовательно, сделать возможным применение теоремы III. Нужно иметь в виду, что здесь не производится сокращение на нуль, что недопустимо, По определению предела функции аргумент х стремится к своему предельному значению, никогда не принимая этого значения; поэтому до перехода к пределу можно произвести сокращение на
множитель, стремящийся к нулю. Имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
lim |
3x 2 |
2x |
|
lim |
x 3x 2 |
lim |
3x 2 |
|
3 0 2 |
|
2 |
. |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2x 2 |
5x |
|
x 2x 5 |
2x 5 |
|
|
||||||||||||||||
x 0 |
|
x 0 |
x 0 |
|
2 0 5 5 |
|
|
|||||||||||||||
Пример 5: Вычислить lim |
|
x2 |
5x 6 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
3x2 9x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Решение. Пределы числителя и знаменателя при x 3 равны нулю: lim |
x 2 5x 6 |
|
||||||||||||||||||||
3x 2 9x |
||||||||||||||||||||||
lim x2 5x 6 32 5 3 6 0, |
lim 3x2 9x 3 32 |
x 3 |
||||||||||||||||||||
9 3 0. |
||||||||||||||||||||||
x 3 |
|
|
|
|
|
|
|
|
|
x |
3 |
|
|
|
|
|
|
|
|
|
|
|
Разложим квадратный трѐхчлен в числителе на линейные множители по формуле |
||||||||||||||||||||||
ax2 bx c a x x |
x x |
2 |
,где x |
1 |
и x |
2 |
|
— корни трѐхчлена. Разложив на множители и |
||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
знаменатель, сократим дробь на x 3 . Используя следствие 4, получим
|
|
|
lim |
x 2 |
5x 6 |
lim |
x 3 x 2 |
lim |
x 2 |
|
3 2 |
|
1 |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3x x 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
3x 2 9x |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
x 3 |
|
|
|
|
x 3 |
|
x 3 |
3x |
|
|
|
|
3 9 |
|
|
|
|||||||||||||||||||||
Пример 6: Вычислить |
lim |
|
|
x 3 |
7x 6 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
3 5x 2 2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
x 2 3x |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Решение. Пределы числителя и знаменателя при x 2, равны нулю: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
lim x3 7x 6 23 |
7 2 6 0, lim 3x3 5x 2 2x 8 23 |
5 22 |
2 2 8 0. |
|||||||||||||||||||||||||||||||||||||
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Разложив числитель и знаменатель на множители и сократив затем на x 2, получим |
|
|||||||||||||||||||||||||||||||||||||||
lim |
|
x 3 7x 6 |
|
|
lim |
x 2 x 2 2x 3 |
lim |
|
x 2 2x 3 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x 2 x 2 3x 4 |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
3x 3 5x 2 2x 8 |
|
x 2 3x 4 |
|||||||||||||||||||||||||||||||||||||
x 2 |
|
|
|
x 2 |
|
|
|
x |
2 |
|
|
|||||||||||||||||||||||||||||
|
|
lim x 2 |
2 lim x 3 |
|
|
|
2 |
2 2 2 3 |
|
5 |
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
lim x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2 |
3lim x |
|
|
2 |
2 |
3 2 |
4 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
4 x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 7: Вычислить |
lim |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2 |
x 3 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
x 2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Решение. Очевидно, что при x 2 функция представляет собой разность двух бесконечно больших величин. Выполнив вычитание дробей, получим дробь, числитель и знаменатель которой
при |
x 2 стремятся к нулю. |
Сократив дробь на x 2 , получим |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
12 |
|
|
|
|
|
lim |
|
x 2 2x 8 |
lim |
|
|
|
x 2 x 4 |
|
|
|
|
|||||||||||||||||||||
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x 2 |
|
|
|
|
4 |
|
|||||||||||||||||||||
|
x 2 x 2 x |
3 8 |
|
|
|
x |
2 |
|
x 3 8 |
x 2 x |
2x |
|
|
|
|||||||||||||||||||||||||||||||||||
|
lim |
|
x 4 |
|
|
|
|
|
|
|
|
|
|
|
|
2 4 |
|
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
x 2 2x 4 |
|
2 2 2 2 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
x 2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Пример 8: Вычислить |
|
lim x3 |
6x 2 |
5x 1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение. Вынося x 3 |
за скобки, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
6 |
|
|
|
|
5 |
|
|
|
|
|
1 |
3 |
|
|
|
6 |
|
5 |
|
1 |
|
|
|
|
|
||||||||||||||||
|
lim |
|
x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim x lim 1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
x |
3 |
|
|
|
|
|
2 |
x |
3 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x x |
|
|
|
|
|
|
|
|
|
x |
x |
|
|
x x |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
(при |
x величины 6 / x, |
|
|
5/ x2 , 1/ x3 — бесконечно малые и их пределы равны нулю). |
|||||||||||||||||||||||||||||||||||||||||||||
Пример 9: Вычислить |
|
lim |
|
|
|
5 |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
x |
|
4x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Решение. При x знаменатель 4x 1 неограниченно растѐт, т.е. является величиной |
|
||||||||||||||||||||||||||||||||||||||||||||||||
бесконечно большой, а обратная величина |
1 |
– бесконечно малой. Произведение |
1 |
|
5 |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
4x 1 |
4x 1 |
|||||||||||||||||||||||||||||||||||||||||||||||
бесконечно малой на ограниченную величину (постоянная—частный случай ограниченной

величины) есть величина бесконечно малая, и предел еѐ при x равен нулю. Следовательно,
lim |
5 |
|
0. |
|
|
|
|
|
|
||
|
|
|
|
||
x 4x 1 |
|
|
|
||
Пример 10: Вычислить lim |
2x 3 |
. |
|||
|
|||||
|
|
|
x 5x 1 |
||
Решение. При x числитель и знаменатель—величины бесконечно большие. Поэтому при непосредственном применении теоремы III получаем выражение / , которое представляет собой неопределѐнность. Для вычисления предела этой функции нужно числитель и знаменатель разделить на x :
|
lim |
2x 3 |
|
lim |
x 2 3 / x |
|
2 0 |
|
2 |
|
|||||||
|
|
x 5 1/ x |
|
|
|
||||||||||||
|
x 5x 1 |
x |
|
5 0 5 |
|||||||||||||
(при x слагаемые |
3/ x, 1/ x — величины бесконечно малые и, следовательно, их пределы |
||||||||||||||||
равны нулю). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 11: Вычислить |
lim |
x 4 |
2x |
2 3 |
. |
|
|
|
|
|
|
|
|||||
|
|
3x |
3 |
5 |
|
|
|
|
|
|
|
|
|||||
|
x |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Разделим числитель и знаменатель на наивысшую степень аргумента в знаменателе, т.е. на x 4 :
lim |
x4 |
2x2 3 |
lim |
x4 1 2 / x2 3 / x4 |
. |
|||
|
3x3 5 |
|
x4 3 / x |
5 / x4 |
|
|||
x |
|
x |
|
|||||
После сокращения в числители величина ограниченная, в знаменателе величина бесконечно малая, следовательно, пределом является величина бесконечно большая.
|
lim |
x 4 2x 2 |
3 |
. |
||||
|
|
|
|
|
||||
|
x |
3x |
3 |
5 |
|
|||
|
|
|
||||||
|
|
|
|
|||||
Пример 12: Вычислить lim x |
|
. |
|
|
|
|
|
|
x 2 4x |
|
|
|
|
|
|||
x |
|
|
|
|
|
|
|
|
Решение. При x данная функция представляет собой разность двух бесконечно больших величин . Умножив и разделив функцию на выражение x 
 x 2 4x, получим
x 2 4x, получим
lim x |
|
|
lim |
x |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
x 2 4x |
|
x 2 |
4x |
|
|
|
|
||||||||||||||||||
x 2 4x |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
x x |
2 |
4x |
|
|
|
|
|
||||||||||||||||||||
x |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
lim |
x 2 |
x 2 4x |
|
lim |
|
|
|
4x |
|
|
|
lim |
4 |
|
|
4 |
2. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
x x |
|
x 2 4x |
|
x x 1 |
1 4 / x |
|
x 1 1 4 / x |
|
|
2 |
|
|||||||||||||||||
34. |
Первый замечательный предел. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
lim |
sin x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
x 0 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Предел отношения синуса бесконечно малой дуги к длине дуги равен единице. Доказательство:
Возьмем круг радиуса 1. Обозначим радианную меру угла АОС через х.

Рассмотрим: 1)Пусть x 0 ; можно считать, что 0 x |
, т.к. x 0 ; |
= sin , = |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
S |
|
|
|
|
|
1 |
sin x 1; |
S |
|
|
|
|
|
1 |
tgx 1 , площадь сектора |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
OBA |
|
|
|
|
|
OAC |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
OAB |
|
1 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
sin x |
1 |
x |
|
1 |
tgx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
2 |
2 |
2 |
разделим это неравенство на |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
1/2sinx >0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
1 |
|
|
x |
|
|
|
|
|
|
|
1 |
|
|
cos x |
sin x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
sin x |
|
|
|
cos x |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Т.к. lim |
|
|
|
|
|
|
|
|
cos = 1, |
lim |
|
|
|
|
|
|
1 = 1, |
то по теореме о 2-х милиционерах => lim |
sin x |
1 . |
|||||||||||||||||||||||||||||||||||||
→0 |
→0 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 x |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
|
|
|
||||||||||
2) пусть x 0 , тогда |
x 0 |
|
|
|
sin x |
|
|
1 при x 0 . |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
Замечание1: |
|
lim |
|
|
x |
|
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Замечание 2: |
|
|
lim |
|
|
|
x |
|
|
1. |
действительно, при → 0, |
∙ → 0. |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
sin( x) |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Замечание 3: |
lim |
tg x |
1 |
или |
|
|
lim |
|
x |
|
1. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
tg x |
|
|
|
|
|
|
|
|
|||||||||||||
Покажем это: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
tg x |
|
|
мы |
|
|
|
|
|
можем |
|
|
представит ь в |
следующем |
виде : |
tg x |
sin x |
, тогда |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos x |
|||
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
lim |
tg x |
|
lim |
sin x |
|
|
|
, но так как cosx 1 |
при |
x 0 , то |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
x |
cos x x |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
x 0 |
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
lim |
|
tg x |
|
lim |
|
sin x |
|
|
|
lim |
|
|
1 |
|
lim |
sin x |
|
1. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
cos x x |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
x 0 |
|
x |
|
|
|
|
x |
0 |
|
|
x |
0 |
|
cos x |
x 0 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Имеет место соотношение ( второй замечательный предел)
|
1 |
x |
lim 1 x |
1 |
|
|
|
e |
|||||
lim 1 |
|
|
e , или |
|||
|
|
|||||
|
x |
|||||
x |
x |
|
x 0 |
|
||
|
|
|
||||
Число e– иррациональное (e ≈ 2,718…, более точное значение e ≈ 2,7182818).
Показательная функция с основанием e называется экспоненциальной. = . Для нее также применяется обозначение y=exp(x).
35.Бесконечномалые функции, теоремы о бесконечномалых. |
|
Функция f x называется бесконечно малой при x a , если lim |
f x 0 . |
x a |
|
Определение. Функция f(x) называется бесконечно малой при x a , если > 0,
, такое, что : − < => ( ) < .
3.4. Свойства бесконечно малых и бесконечно больших функций:
1. |
Произведение ограниченной при x a функции на б.м. при x a , есть функция б.м. при |
||||||||||||
|
x a . |
|
|
|
|
|
|
|
|
|
|
|
|
2. |
Произведение конечного числа б.м. при x a функции есть б.м. при x a функция. |
||||||||||||
3. |
Произведение постоянной на б.м. при x a функцию есть б.м. при x a функция. |
|
|
|
|||||||||
|
Определение: Функция f x называется бесконечно большой при x a , если |
|
|
|
|
||||||||
|
lim f x |
т.е |
lim f x , или lim f x . |
|
|
|
|
|
|
|
|||
|
x a |
|
x a |
|
|
x a |
|
|
|
|
|
|
|
4. |
Если функции |
f x |
и x - бесконечно малые при x a , то их сумма f x x |
||||||||||
|
при x a также является бесконечно малой. |
|
|
|
|
|
|
|
|||||
5. |
Если функция |
f x |
– бесконечно малая при x a , а F x - ограниченная функция, то их |
||||||||||
|
произведение f x F x |
есть функция бесконечно малая. |
|
|
|
|
|
|
|
||||
6. |
Произведение конечного числа бесконечно малых функций есть величина бесконечно малая. |
||||||||||||
|
Если при x a функция |
|
|
lim f x |
A |
|
x - |
||||||
7. |
f x имеет конечный предел x a |
,а функция |
|||||||||||
|
бесконечно большая, то |
|
f x |
|
|
|
|
|
|
|
|
||
|
lim f x |
x , |
lim |
0. |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||
|
x a |
x |
|
|
|
|
|
|
|
||||
|
x a |
|
|
|
|
|
|
|
|
|
|
||
8. |
Если функция |
f x – бесконечно малая при x a , то функция |
|
1 |
- бесконечно |
||||||||
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
большая, причем предполагается, что в окрестности точки а функция f(x) не обращается в |
||||||||||||
|
нуль. Наоборот, если при x |
a функция ( )- бесконечно большая, то функция |
1 |
|
|
- |
|||||||
|
( ) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
бесконечно малая. |
|
|
|
|
|
|
|
|
|
|
|
|
36. |
Связь между функцией, ее пределом и бесконечномалой. |
|
|
|
|
|
|
|
|||||
Между бесконечно малой функцией и функцией, имеющей конечный предел, существует следующая зависимость.
Теорема: Если функция f x имеет конечный предел при x a , то ее можно представить
в виде суммы постоянной и бесконечно малой функции при x a , т.е. если lim f x A , то
x a
в окрестности точки a f(x)=A + α(x), где limx→a α x = 0
Теорема( обратная): если функция f x может быть представлена в виде суммы
постоянной и бесконечно малой функции при x a , то эта функция имеет конечный предел при x a , и этот предел равен значению постоянной, т.е. если то f(x)=A +  (x), где
(x), где 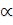 (x) –
(x) –
бесконечно малая функция, то lim f x A .
X a
37. Эквивалентные бесконечномалые и их использование для вычисления пределов.
Сумма, разность и произведение двух бесконечно малых функций есть функция бесконечно малая. Отношение же двух бесконечно малых функций может вести себя различным образом, т.е: быть конечным числом, быть бесконечно малой, или бесконечно большой функцией, или вообще не стремиться ни к какому пределу.
Пусть x и x - бесконечно малые функции при x a . Рассмотрим lim |
x |
A . |
|
|
x a |
x |
|
1. |
Если конечное A 0 , то x и x - б.м. одного порядка малости; |
|
|
2. |
Если конечное A 0 , то порядок б.м. x выше порядка x . |
|
|
3. |
Если A , то x ниже порядка x . |
|
|

4. |
Если A не существует, то x и x несравнимые б.м. функции. |
5. |
Если A 1, то x и x эквивалентные б.м. при x a функции (обозначается x |
 x ).
x ).
4.6. Теоремы об эквивалентных бесконечно малых функциях
Теорема 1: Предел отношения двух бесконечно малых функций не изменится, если каждую или одну из них заменить эквивалентной ей бесконечно малой функцией. Теорема 2: Разность двух эквивалентных бесконечно малых функций есть бесконечно малая более высокого порядка, чем каждая из них.
Теорема 3. Сумма конечного числа бесконечно малых функций разного порядка эквивалентна слагаемому высшего порядка.
4.7. Таблица эквивалентных функций (при → 0) sin x x;
tgx x; arcsin x x; arctgx x; ln 1 x x;
1 cos x x2
2
ex 1 x
a x 1 x ln a;
1 m n 1 mx
38. Свойства функций, непрерывных на отрезке.
Теорема 1(Вейерштрасса): Если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значений.
Изображенная на рисунке функция принимает свое наибольшее значение М в точке  , а
, а
наименьшее значение m в точке  . Для любого значения
. Для любого значения 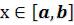 имеет место неравенство:
имеет место неравенство:
.

Теорема 2( БольцаноКоши): Если функция y=f(x) непрерывна на отрезке |
и принимает на |
|||
его концах неравные значения f(a)=A, и f(b)=B, то на этом отрезке |
она принимает все |
|||
промежуточные значения между А и В. |
|
|
|
|
Следствие: Если функция y=f(x) непрерывна на отрезке |
и на его концах принимает |
|||
значения разных знаков, то внутри отрезка |
найдется хотя бы одна точка с, в которой |
|||
данная функция f(x) обращается в нуль : |
f( c)=0. |
|
|
|
|
|
|
|
|
Данное утверждение лежит в основе метода «половинного деления», который используется для нахождения корня уравнения f(x)=0.
Метод половинного деления:
Для решения уравнения f(x)=0 с заданной точностью , необходимо :
1.Подобрать отрезок  , такой, что на этом отрезке функция непрерывна и f(a)
, такой, что на этом отрезке функция непрерывна и f(a) f(b)<0.
f(b)<0.
2.Вычислить 
3.Если f(x)=0, то х- корень уравнения
4.Если  , то если f(a)
, то если f(a) , то b=x , иначе a=x
, то b=x , иначе a=x
5.Если  , то х найден, иначе идти на пункт 2.
, то х найден, иначе идти на пункт 2.
39.Непрерывность функции в точке, классификация точек разрыва
Функция y=f(x) называется непрерывной в интервале (а;b), если она непрерывна в каждой точке этого интервала.
Функция y=f(x) называется непрерывной на отрезке [а;b], если она непрерывна в интервале
(а;b) и в точке |
х=а непрерывна справа ( т.е. |
lim f (x) f (а) |
), а в точке х=b непрерывна |
||
|
|
|
|
x а 0 |
|
слева (т.е. |
lim |
f (x) f (b) |
). |
|
|
|
x b 0 |
|
|
|
|
Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции. Если х=х0 – точка разрыва, в ней не выполняется по крайней мере одно из условий определения непрерывности функции.
Все точки разрыва разделяются на точки разрыва первого и второго рода.
Определение: Точка разрыва х0 называется точкой разрыва первого рода функции y=f(x), если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы), т.е.
lim f (x) А1 |
и |
lim f (x) |
А2 . |
x x0 0 |
|
x x0 0 |
|
При этом: |
|
|
|
1) если А1=А2 , и f(x) ≠ 1, то точка х0 |
называется точкой устранимого разрыва; |
||
2) если 1 ≠ 2, то х0 |
называется точкой конечного разрыва, а величину 1 − 2 называют |
||
скачком функции. |
|
|
|
Точка разрыва х0 |
называется точкой разрыва второго рода функции y=f(x), если по крайней |
||
мере один из односторонних пределов (слева или справа) не существует или равен бесконечности.

Пример1: |
|
|
|
|
|
|
|
Исследовать функцию = |
1 |
на непрерывность в точке х=2. |
|
|
|
|
|
−2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
В точке х=2 функция не определена. |
|||||
Предел слева: |
|
|
|
|
|
|
|
|
|
lim |
1 |
|
|
= −∞ |
|
|
|
|
|
|
|
||
|
|
|
( − 2) |
||||
|
|
→2−0 |
|
|
|||
|
|
Предел справа: |
|
|
|
|
|
|
|
lim |
1 |
|
|
= +∞ |
|
|
|
|
|
|
|
||
|
|
( − 2) |
|||||
|
|
→2+0 |
|
||||
В точке х=2 функция имеет разрыв второго рода.
40. Определение производной, ее физический и геометрический смысл.
Понятие производной
Пусть функция y=f(x) определена в некоторой окрестности точки x0 . Дадим аргументу x0 приращение x , тогда функция получит приращение y f x0 x f x0 .
Отношение y показывает среднюю скорость изменения функции y относительно аргумента x
x
на промежутке x0 ; x0 x .
Определение: Если существует конечный предел отношения приращения функции к приращению
аргумента |
при |
x 0 , |
то этот |
предел называется |
производной функции в |
точке |
x0 |
и |
||||||
обозначается ′ ( ) |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
0 |
|
|
|
|
f x0 x f x0 |
|
|
|
||
|
|
|
|
f |
' |
(x0 ) lim |
|
|
|
|||||
|
|
|
|
|
x |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
Для обозначения |
производной в |
точке |
применяются |
следующие обозначения: |
′ |
|
, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
′ , |
′ |
= 0 |
, |
, |
|
|
|
|
|
|
|
|
||
0 |
|
|
0 |
|
= 0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функция, имеющая производную в каждой точке интервала, называется дифференцируемой на этом интервале. Операция нахождения производной функции называется дифференцированием.
Определение: Закон, по которому каждой точке x (a,b) ставится в соответствие производная в
этой точке, называется производной функции на множестве (a,b).
Для обозначения производной функции применяются следующие обозначения:
′ |
, |
′ , |
′ |
, |
, |
|
|
Геометрический смысл производной Касательной к данной кривой в данной точке М
называется предельное положение МТ секущей MN, проходящей через точку М, когда вторая точка секущей N, неограниченно приближается по кривой к точке М.
Рассмотрим график непрерывной функции y=f(x). Пусть в точке x0 функция имеет невертикальную
