Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Кубанский государственный технологический университет

Предмет:

Высшая математика

Файл:

отвкты на математику

.pdf

Скачиваний:

Добавлен:

22.05.2015

Размер:

2.27 Mб

Скачать

☆

1 / 61 2 3 4 5 6 > Следующая >>>

ВОПРОСЫ К ЭКЗАМЕНАМ 1 СЕМЕСТР

1.Матрицы и виды матриц. Сложение матриц и умножение на число

2.Умножение матриц.

3.Транспортирование матриц.

4.Вычисление определителей.

5.Правило Крамера

6.Обратная матрица и способы вычисления.

7.Решение системы как матричное уравнение .

8.Миноры, алгебраические дополнения, вычисления определителя разложением по строке.

9.Метод Гаусса

10.Векторы, декартова система координат, выражение вектора через начало и конец , длина вектора.

11.Сумма . разность , умножение на число вектора в геометрической и координатной форме.

12.Скалярное произведение: определение , выражение через координаты множителей, приложение.

13.Векторное произведение.

14.Смешанное произведение.

15.Взаимное расположение векторов.

16.Прямая по точке и нормам на плоскости.

17.Прямая по точке и направляющему вектору на плоскости.

18.Прямая по двум точкам (уравнение прямой в отрезках).

19.Прямая с угловым коэффициентом.

20.Угол между прямыми и расстояние от точки до прямой.

21.Эллипс.

22.Гипербола.

23.Парабола.

24.Плоскость по точке и нормали.

25.Плоскость по точке и двум направляющим.

26.Плоскость по трем точкам и уравнение в отрезках.

27.Угол между плоскостями и расстояние от точки до плоскости.

28.Прямая в пространстве по точке и направляющему вектору.

29.Прямая в пространстве по двум точкам.

30.Прямая по точке перпендикулярно плоскости.

31.Перевод прямой из общего в канонический вид, из канонического в общий.

32.Предел числовой последовательности, предел функции в точке, односторонние пределы.

33.Правила вычисления предела. Примеры.

34.Первый замечательный предел.

35.Бесконечномалые функции, теоремы о бесконечномалых.

36.Связь между функцией, ее пределом и бесконечномалой.

37.Эквивалентные бесконечномалые и их использование для вычисления пределов.

38.Свойства функций, непрерывных на отрезке.

39.Непрерывность функции в точке, классификация точек разрыва

40.Определение производной, ее физический и геометрический смысл.

41.Правила вычисления производных.

42.Вывод производных некоторых элементарных функций(на выбор студента)

43.Логарифмическая производная. Примеры.

44.Производная нефвно заданной функции и функции заданной параметрически.

45.Уравнение касательной к графику функции.

46.Исследование функции на монотонность и экстремумы с помощью производной.

47.Правило Лопиталя.

48.Теорема Ролля.

49.Теорема Лагранжа.

50.Теорема Коши.

1.Матрицы и виды матриц. Сложение матриц и умножение на число

Матрицей размера m x n называется прямоугольная таблица чисел, состоящая из m строк и n столбцов. Обозначается такая матрица А mn . Элемент, стоящий на пересечении i строки и j

столбца обозначается a ij , i=1,..., m, j=1,..., n:

Матрица называется квадратной, если число строк равно числу столбцов и обозначается Аn , где n - порядок матрицы.

Элементы a11, a22 ,...ann ,стоящие на диагонали квадратной матрицы, идущей из левого верхнего в правый нижний угол, называются главной диагональю матрицы.

Квадратная матрица, вне главной диагонали которой находятся нули, называется

диагональной матрицей.

Квадратная матрица, под главной диагональю которой находятся нули, называется

верхнетреугольной.

Диагональная матрица, все элементы главной диагонали которой равны единице, называется единичной и обозначается Е.

Матрица, все элементы которой равны 0,называется нулевой и обозначается О.

Примеры: Определить тип матрицы:

		2		0		0		1		3	5	0		1		0	0
		2		0		0								1		0	0
			0	3		0			0	2 3		4			0	1	0	0		0
D=							; B=						; E3=								; A23=
D=							; B=		0	0 4		7	; E3=					; O2=	0	0	; A23=
			0	0		5			0	0 4		7			0	0	1		0	0
			0	0		5			0	0	0	6			0	0	1
									0	0	0	6
2			4 5		8

	3		1 1		7
	3		1 1		7

Решение: D-диагональная; В-верхнетреугольная; Е 3 -единичная третьего порядка; О 2 -нулевая второго порядка; А 2 4 -прямоугольная

Матрица, содержащая один столбец, называется вектором, или векторомстолбцом. Матрица, содержащая одну строку, называется вектором, или

вектором-строкой.

Примеры: А-вектор-столбец; В-вектор-строка

	3
			2 5 .
А=	4	; В= 3 0	2 5 .
	7
	7

Матрицы равны между собой, если они одинакового размера и равны все соответствующие элементы этих матриц. А=В, если aij bij , где i=1, m; j=1, n .

Квадратная матрица A, для которой A T =A, называется симметричной. Элементы такой матрицы, расположенные симметрично относительно главной диагонали, равны.

Умножение матрицы на число:

По определению, чтобы умножить матрицу на число, нужно умножить на это число каждый элемент этой матрицы.

k A =k ...

am1

...	a	ka
	1n		11
...	...	...
...
	amn	kam1

...	ka
	1n
...	...
...
...	kamn

Сложение матриц:

Суммой двух матриц одинаковой размерности, называется матрица той же размерности, каждый элемент которой равен сумме соответствующих элементов слагаемых.

a	...	a	b
11		1n	11
А+В= ...	...	...	...
	...
am1	...	amn	bm1

...	b	a		b	...	a		b
	1n		11	11			1n	1n
...	...	...			...			...
...	b	a	m1	b	...	a	mn	b
	mn		m1	m1			mn	mn

2.Умножение матриц.

. Пусть заданы две матрицы A и B, причем число столбцов первой из них равно числу строк второй. Если

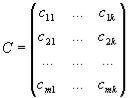
то произведением матриц A и B, называется матрица

элементы которой вычисляются по формуле

c ij =a i1 b 1j + a i2 b 2j + ... +a in b nj , i=1, ..., m, j=1, ..., k.

другими словами, элемент c ij равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В.

Произведение матриц A и B обозначается AB, т.е. C=AB. Матрица-результат имеет количество строк, равное количеству строк левого множителя и количество столбцов, равное количеству столбцов правого множителя.

Примеры: Для данных матриц выполнить взаимные умножения:

			4			1		0	2
А= 1 2
А= 1 2	3 ; В=		5	; D=			4 1		3 .
			6				0	2
			6				0	2	4
Решение:
					4
А В 1 2						1 4			5 3 6 32
А В 1 2		3			5	1 4		2	5 3 6 32
					6
					6

	4		4 1 4 2				4 3	4	8 12
		1 2
В А	5	1 2	3	5	1	5 2	5 3	5	10	15
	6			6	1	6 2		6	12	18
	6			6	1	6 2	6 3	6	12	18

			1		0	2
А D 1								7	8 8 ; D A выполнить невозможно.
А D 1		2	3	4	1	3		7	8 8 ; D A выполнить невозможно.
				0	2
				0	2	4
1 0			2		4	8

D B	4	1	3		5		3	; B D выполнить невозможно
	0 2		4		6		34
	0 2		4		6		34

Произведение матриц, вообще говоря, зависит от порядка сомножителей, т.е.

А В В А в общем случае. Две матрицы A и B называются перестановочными, если А В В А

3. Транспортирование матриц.

Чтобы транспонировать матрицу, необходимо элементы первой строки записать в первый столбец, элементы второй строки во второй столбец и т.д..

a	a
11	12
a21	a22
A
...	...

	am2
am1	am2

... a1n

... a2n

... ...

... amn

при транспонировании получим:

		а		а			...		а
			11		21					m1
	T	a12		a22 ...					am2
А
		...		... ...					...

				a2n ...
		a1n		a2n ...					anm
Примеры: Транспонировать матрицы:
												3	Т			2			0	Т
			3	5		Т	3			2		5				2		0	0
		А Т =	3	5			3			2		5	= 3 5	7	4 . D Т =		0	4 0
		А Т =					=				; В Т =		= 3 5	7	4 . D Т =		0	4 0		=
								5		7		7
			2	7				5		7		7					0	0	5
												4					0	0	5
												4
2		0	0
	0	4	0
	0	4	0	.
	0	0	5
	0	0	5

4.Вычисление определителей.

Вычисление определителей второго и третьего порядка

Квадратной матрице А n порядка n можно поставить в соответствие число, обозначаемое det А

(или А ,

или

), называемое ее определителем (детерминантом), и вычисляемое по следующим

схемам:

det А 1 = а11

а11

det А

= а11

а12

= +=

а21

а22

а11

а12

а13

detА 3 = а21

а22

а23 =

а31 а32 а33

а11 а22 а33 а12 а23 а31 а21 а32 а13 - а13 а22 а31 а12 а21 а33 а23 а32 а11

5.Правило Крамера

Справедливо следующее утверждение (формулы Крамера):

Если определитель =det A матрицы системы Ax=В отличен от нуля, то система

имеет единственное решение х1 ; х2 ;...; хn , определяемое формулами Крамера: хi i , где i=1,2, ., n,

где i - определитель матрицы n -го порядка, полученной из матрицы A системы заменой i -го столбца столбцом свободных переменных b.

Применим правило Крамера для решения системы двух линейных уравнений с двумя неизвестными.

	a x b y c
Рассмотрим систему:	1	1	1 ,
	a2 x b2 y c2
где

- главный определитель;

- вспомогательные определители. Они получаются заменой в

главном определителе колонки коэффициентов при х ( 1) и при y

( 2) колонкой свободных

членов.

Решение системы по правилу Крамера имеет вид:

, y

, 0 .

Для систем трех уравнений с тремя неизвестными

a11x a12 y a13z b1a21x a22 y a23z b2

a31x a32 y a33z b3

правило Крамера имеет вид:

	x	1		, y				2	, z					3	,
	x			, y					, z						,

где
a11	a12		a13									b1		a12		a13					a11		b1	a13						a11		a12	b1
a11	a12		a13									b1		a12		a13					a11		b1	a13						a11		a12	b1
a21	a22		a23			,		1				b2		a22		a23		,	2		a21		b2	a23		,		3		a21		a22	b2	, 0
a31	a32		a33									b3		a32		a33					a31		b3	a33						a31		a32	b3
																									2х1 3х2						8
																											х1 х2				1
	Пример 4. Решить систему по формулам Крамера:																										х1 х2				1	.
	Пример 4. Решить систему по формулам Крамера:																															.
								2			3									8	3								2		8
								2			3		2 3 5; 1							8	3	8 3 5; 2							2		8	2 8 10;
Решение:								1			1									1	1								1		1
Решение:
х 1					5		1; х					2				10	2
х 1							1; х			2		2					2
	1		5							2						5
			5													5

х1 1

Ответ: х2 2

6.Обратная матрица и способы вычисления.

1.Вычислить определитель матрицы detA ( detA 0 ,в противном случае обратная не существует.)

		A	...	A
		11		1n
2. Составить матрицу из алгебраических дополнений элементов:	А* ...		...	...
			...
	An1		...	Ann

	А*	1
3. Каждый элемент полученной матрицы разделить на определитель:
	det A		det A

	A ...		A
	11			1n
... ... ...
			Ann
An1 ...			Ann
4. Транспонировать										полученную			матрицу:
					A	...	A T			A	...	A
A 1		1			11		1n	1		11		n1
					...	...	...		...		...	...
					...	...	...		...		...	...
		det A						det A
				An1		...	Ann		A1n		...	Ann

5.	Результат проверить, умножив А на А 1 .
Пример: Для матрицы А=							2			3			найти обратную.
Пример: Для матрицы А=													найти обратную.
								1
								1		1
Решение:
			2	3	2 3 5
1.Находим detA=			2	3	2 3 5
		1		1
2.Составляем матрицу				А* : А				1, А					( 1) 1, А						3, А				2 , поэтому А*				1
2.Составляем матрицу				А* : А				1, А					( 1) 1, А						3, А				2 , поэтому А*
						11						12						21			22
																										3
															1		1
												А	*							0,2			0,2
													*		5		5

3.Делим элементы на определитель:																				0,6
3.Делим элементы на определитель:
											det A				3		2						0,4
															5

																	5
4.Транспонируем полученную матрицу: А 1															0,2				0,2 Т			0,2		0,6
4.Транспонируем полученную матрицу: А 1
																			0,4					0,4
															0,6				0,4			0,2		0,4
				0,2		0,6				2				3		0,2 2 0,6 ( 1)							0,2 3 0,6 1			1
5.Проверка: А 1 А
				0,2		0,4						1					2 0,4 ( 1)						0,2 3				0
				0,2		0,4						1		1		0,2	2 0,4 ( 1)						0,2 3		0,4 1		0
	0,2		0,6
Ответ:	А 1				.

	0,2		0,4
					1		2		3
						2	2		3
Пример: Для матрицы А=						2	2		3	найти обратную.
						3	3		4
						3	3		4

Решение:

	1	2	3
Находим detA=	2	2	3	8 18 18 18 9 16 1
	3	3	4

Составляем матрицу
						3									2		3						2 2						2		3
А* : А ( 1)2					2	3	1, А ( 1)3								2		3	1.А ( 1)4					2 2		0, А ( 1)3				2		3		1,
11					3	4			12						3		4		13				3	3		21			3		4
					3	4									3		4						3	3					3		4
													1		2							2 3								1		3
А ( 1)4		1 3				5, А ( 1)5							1		2	3, А ( 1)4						2 3			0, А ( 1)5					1		3		3,
22		3		4				23					3		3				31			2		3		32				2		3
		3		4									3		3							2		3						2		3
												1					1		0
	1			2
А33 ( 1)6	1			2		2.		поэтому А*						1	5				3
	2			2										0			3		2
														0			3		2
															1				1		0
											А	*
												*
Делим элементы на определитель:															1				5		3
Делим элементы на определитель:											det A				1				5		3
											det A
															0				3	2
															1				1		0 Т	1			1	0
Транспонируем полученную матрицу: А 1
Транспонируем полученную матрицу: А 1																	1		5		3			1	5	3
																	0		3 2					0
																	0		3 2					0	3 2
Проверка:
	1					1		0 1 2 3							1 2						2 2				3 3		1 0				0
А 1 А
А 1 А			1			5		3		2 2 3					1 10 9						2 10 9			3 15		12		0 1			0			Е3
			0			3 2				3 3 4							6		6		6 6				9 8			0 0			1
			0			3 2				3 3 4							6		6		6 6				9 8			0 0			1

		1		1	0
Ответ:	А 1		1	5	3	.

			0	3	2
			0	3	2

7.Решение системы как матричное уравнение .

Решение матричных уравнений

Рассмотрим системы, число уравнений которых m равно числу переменных n и матрица системы А является невырожденной, т.е. detА 0 .Если матрица системы невырождена, то у нее существует обратная матрица А 1 . И тогда для решения матричного уравнения AX=B,

необходимо обе части этого уравнения слева умножить на А 1	Получаем решение системы в
виде: X A 1 B .

	2х1 3х2			8
		х1	х2	1
Пример 2: Решить систему, как матричное уравнение:					.

Решение:

																								2		3			х				8
																													1

			1.				Запишем систему в матричном виде:																	1 1					х2				1	.
			1.				Запишем систему в матричном виде:																											.
			2.					Для			матрицы							системы					2		3		найдем					обратную			матрицу:
			2.					Для			матрицы							системы					А				найдем					обратную			матрицу:
																								1	1
																								1	1
А 1			0,2		0,6
А 1									,
						0,4
			0,2			0,4
			3.				Решение												системы						ищем									в	виде:
	х		А 1			8					0,2			0,6					8		0,2 8 0,6 1						1
	1		А 1

	х2					1					0,2				0,4				1		0,2 8 0,4 1						2	.
					х				1
					1
					х2
	Ответ:				х2				2			.
	Ответ:											.
	Пример 3: Решить матричное уравнение:
		1 2			3				х			6
									1
			2 2		3				х2					7
			3 3		4				х3					9
			3 3		4				х3					9		.
																.
	Решение: Для матрицы системы А найдем обратную матрицу:
												1				2 3								1				1		0

									А				2			2 3							А 1		1 5					3
													3			3 4									0			3 2
													3			3 4									0			3 2
			1.				Решение										системы						ищем			в					виде:				x A 1 B .
	х					6					1				1		0 6				6 7 0							1
	1		А 1
	х2		А 1			7					1 5 3									7		6	35 27				2
	х3					9					0				3			2		9		0	21 18					3
	х3					9					0				3			2		9		0	21 18					3		.
																														.
				х							1
					1					2
				х2						2
											3
	Ответ:			х3							3		.
	Ответ:												.

8.Миноры, алгебраические дополнения, вычисления определителя разложением по строке.

Опр: Минором М ij элемента aij определителя n-го порядка называется определитель (n-1)-го

порядка ,полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится элемент аij .

Опр: Алгебраическим дополнением Аij элемента aij называется его минор, умноженный на число

(-1) i j :	A ( 1)i j M	ij
	ij	ij

Теорема: Определитель матрицы равен сумме произведений элементов любой его строки (столбца) на их алгебраические дополнения.

Разложение определителя по любой (i-й, где i=1,2,…n) строке:

	n	n
det Аn аi1 Ai1 ai 2 Ai 2 ... ain Ain	aij Aij	( 1)i j aij Aij
	j 1	j 1

Разложение определителя по любому (j-му, где j=1,2,…n) столбцу:

														n					n
detA n			a1 j	A1 j		a2 j A2 j			... anj Anj				aij Aij					( 1)i j			aij	Aij
														i 1				i 1
Пример: Найти						минор		М 32		и	алгебраическое						дополнение				А32	элемента а32 матрицы А=
2		2	0	1
	2	1	3	4
	2	1	3	4
	1	1	0	2	.
	1	1	0	2

	5	2	1	0
	5	2	1	0
Решение:
								2	0	1		2	0	1
							2
							2
							2	1	3	4
Найдем минор: М 32							2	1	3	4	=	2	3	4	=0+0+2-15-8-0=-21;
							1	1	0	2		5	1	0
							5	2	1	0		5	1	0
							5	2	1	0			( 1)3 2				М		1 ( 21) 21
Найдем алгебраическое дополнение: А													( 1)3 2				М	32	1 ( 21) 21
											32							32
Ответ:			М 32 21 , А32					21
															2		2	0	1
																2	1	3	4
																2	1	3	4
Пример: Вычислить определитель матрицы А=																1	1	0	2	.
																1	1	0	2

																5	2	1	0
																5	2	1	0

Решение: Вычислим определитель разложением по третьему столбцу:

det A ( 1)1 3 а			М		13	( 1)2 3	а		23	М	( 1)3 3 а		33	М	33	( 1)4 3	а	43	М	43
		13			13				23		23		33		33			43		43
		2	1					2		2	1
	2	2	1					2		2	1
0 М13 3	1	1	2	0 М 33 1				2		1	4	3 9 ( 3) 24.
	5	2	0					1		1	2

Ответ: detA=-24

Свойства определителя:

1.Определитель матрицы равен определителю транспонированной матрицы. det A=detA Т .

2.При перестановке местами двух параллельных строк или столбцов определитель меняет свой знак на противоположный.

3.Определитель, имеющий две одинаковые , или две пропорциональные строки или столбца равен нулю.

1 / 61 2 3 4 5 6 > Следующая >>>

Соседние файлы в предмете Высшая математика

#
22.05.2015169.47 Кб12Математика первый семестр 2012-13.doc
#
20.03.2016994.82 Кб105Математика шпоры 7 шрифт.doc
#
22.05.2015629.25 Кб25Математика. Задачи к экзамену..doc
#
22.05.20151.18 Mб21Математика.doc
#
20.03.20161.18 Mб16МИППС Математика 2 ч.doc
#
22.05.20152.27 Mб23отвкты на математику.pdf
#
22.05.2015192.67 Кб383Практикум. Дискретная математика..pdf
#
04.11.20188.04 Mб51УЧЕБНИК ПО МАТЕМАТИКЕ.doc

...	b	a		b	...	a		b
	1n		11	11			1n	1n
...	...	...			...			...
...	b	a	m1	b	...	a	mn	b
	mn		m1	m1			mn	mn

...	b	a		b	...	a		b
	1n		11	11			1n	1n
...	...	...			...			...
...	b	a	m1	b	...	a	mn	b
	mn		m1	m1			mn	mn

...	b	a		b	...	a		b
	1n		11	11			1n	1n
...	...	...			...			...
...	b	a	m1	b	...	a	mn	b
	mn		m1	m1			mn	mn