8.2 Внецентренное растяжение (сжатие)

Рисунок 8.5 - Внецентренное растяжение стержня

Точка приложения силы называется центром давления, а расстояние от центра тяжести до точки приложения силы называется эксцентриситетом и обо-

значается «е».

8.2.1. Определение нормальных напряжений при внецентренном

растяжении (сжатии)

Пусть точка приложения внешней силы имеет координаты xF, yF (рису-

нок 8.5). При такой схеме нагружения внутренние силовые факторы в произ-

вольном поперечном сечении бруса равны:

где yF, zF - координаты точки приложения силы.

Таким образом, если перенести силу P в центр тяжести сечения(рисунок

8.5.б), то внецентренное растяжение(сжатие) может быть сведено к осевому растяжению (сжатию) и чистому косому изгибу.

148

Выражение в скобках в уравнении(8.15) показывает во сколько раз на-

пряжения при внецентренном растяжении(сжатии) больше напряжений цен-

трального растяжения. Переменными в формуле (8.15) являются два последних слагаемых, отражающих влияние изгиба. Так как при изгибе максимальные на-

пряжения возникают в точках, наиболее удаленных от нейтральной оси, то для определения наиболее опасных точек при внецентренном растяжении или сжа-

тии необходимо определить положение нейтральной оси.

8.2.2Определение положения нейтральной линии при внецентренном растяжении (сжатии)

Обозначим коордиаты точек нейтральной оси xo, yo. Для определения по-

ложения нейтральной оси приравняем нулю выражение (8.15) и после сокраще-

ния на F/A получим уравнение нейтральной линии:

Из уравнения (8.17) следует, что нейтральная линия при внецентренном растяжении (сжатии) не проходит через центр тяжести сечения. Нейтральная линия отсекает на осях координат отрезки xн , yн (рисунок 8.6). Чтобы найти от-

резок xн , отсекаемый на оси x, надо в уравнении (8.16) положить xo= xн, yo=0.

Тогда получим:

Из формулы (8.17) видно, что точка приложения силы и нейтральная ли-

ния всегда расположены по разные стороны от центра тяжести сечения, причем положение нейтральной линии определяется координатами точки приложения силы (рисунок 8.6).

Для определения наиболее опасных точек необходимо провести -каса тельные к контуру сечения параллельные нейтральной линии. Наиболее уда-

149

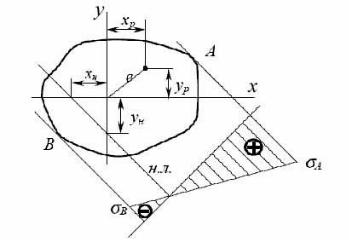
ленные точки касания А и В, расположенные в растянутой и сжатой зоне, яв-

ляются наиболее опасными (рисунок 8.6). Эпюра напряжений строится на оси,

перпендикулярной к нейтральной линии сечения и ограничена прямой линией.

Условие прочности имеет следующий вид:

где yF, zF - координаты опасной точки, а [σ] - допускаемое напряжение на растяжение и сжатие.

Рисунок 8.6 - Определение положения нейтральной линии

В тех случаях, когда в наиболее удаленной от нейтральной линии точке действует напряжение сжатия, а материал элемента конструкции хрупкий,

опасной может быть точка, в которой действует наибольшее растягивающее напряжение.

8.2.3 Определение положения ядра сечения

При приближении точки приложения силы к центру тяжести сечения (xн и yн по абсолютной величине возрастают) нейтральная линия будет удаляться от центра. При этом в сечении увеличивается доля напряжений одного знака, так как уменьшаются напряжения от изгиба. В пределе при xF = yF=0 нейтральная линия удаляется в бесконечность. В этом случае будет иметь место центральное растяжение (сжатие) бруса.

150

Всегда можно найти такое положение точки приложения силы, при кото-

ром нейтральная линия будет касаться контура сечения, нигде не пересекая его.

В этом случае в сечении напряжения будут только одного знака. Зона вблизи центра тяжести сечения, приложение продольной нагрузки в которой вызывает появление во всех точках сечения напряжений только одного знака, называется

ядром сечения. До тех, пока точка приложения силы находится внутри ядра,

нейтральная линия не пересекает контур сечения, и напряжения во всем сече-

нии будут одного знака. Если точка приложения силы расположена вне ядра, то нейтральная линия пересекает контур сечения, и тогда в сечении будут дейст-

вовать напряжения разного знака. Указанное обстоятельство необходимо учи-

тывать при расчете элементов конструкций из хрупких материалов, плохо вос-

принимающих растягивающие нагрузки. В этом случае необходимо приклады-

вать внешние силы так, чтобы во всем сечении действовали только напряжения сжатия. Для этого точка приложения равнодействующей внешних сил должна находиться внутри ядра сечения.

Для построения ядра сечения необходимо задаться различными положе-

ниями нейтральной оси и вычислить соответствующие точки приложения силы

F по формулам (8.17).

Вычисленные координаты xF, yF определяют точки, лежащие на границе ядра сечения (рисунок 8.7).

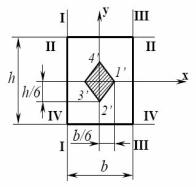
Рис. 8.7 - Определение положения ядра сечения для прямоугольного сечения

151

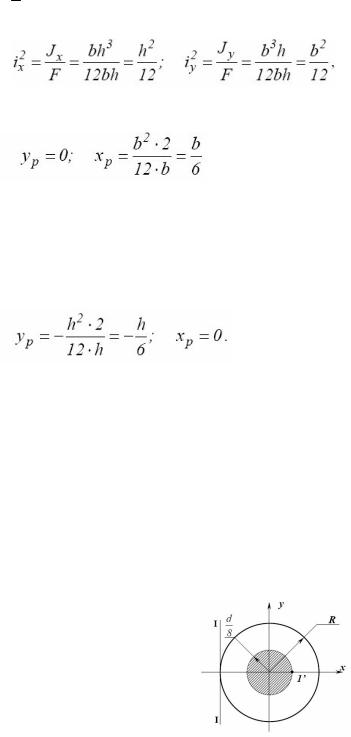
Построим ядро сечения для прямоугольного сечения (рисунок 8.8) со сто-

ронами b и h. Совместим вначале нейтральную линию с одной из сторон пря-

моугольника (положение I-I). При этом координаты нейтральной линии равны

xí = - b ; yí = ¥ , а учитывая, что

2

(8.18)

Из формулы (8.17) получим для точки 1'

Совместим теперь нейтральную линию с другой стороной (положение II-

Аналогично определяем координаты точек 3' и 4'.

Так как при переходе нейтральной линии с одной стороны на другую она поворачивается вокруг угловой точки сечения, то точка приложения силы пе-

ремещается по прямой, образуя контур ядра. Таким образом, ядро сечения пря-

моугольника представляет собой ромб с диагоналями, равными одной трети со-

ответствующей стороны.

Построим ядро для круглого сечения (рисунок 8.8).

Рисунок 8.8 - Ядро сечения для круглого сечения

В круге все центральные оси являются главными, поэтому при касании нейтральной линии I-I в любой точке окружности точка I' ядра сечения будет

152

лежать на том же диаметре с противоположной стороны относительно центра

тяжести. Положение нейтральной линии определяется координатами: xí = R , yí = ¥ .

Тогда координаты точки 1' ядра

Таким образом, ядро сечения для круглого сечения представляет собой круг с радиусом R/4 или d/8.

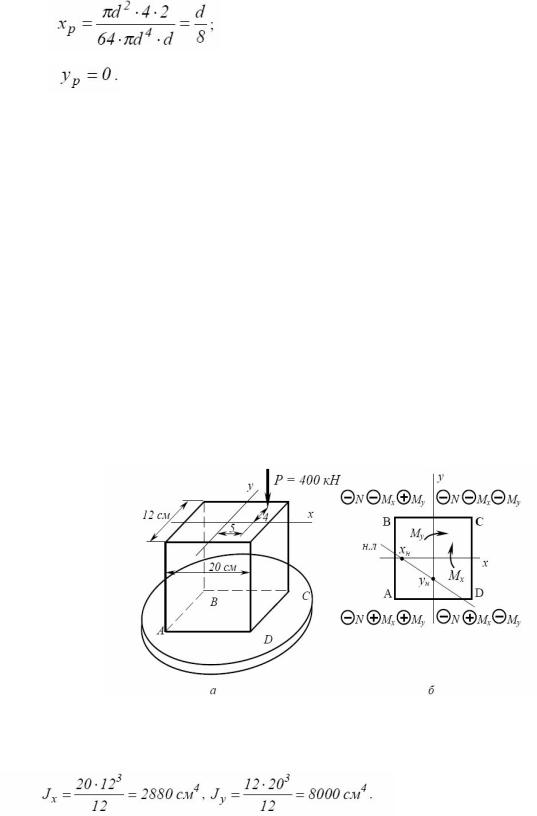
Пример

Стержень нагружен внецентренно приложенной силой Р=400кН (прису-

нок 8.9). Определить напряжения в точках А, В, С и D. Размеры сечения приве-

дены на рисунке. Определить положение нейтральной оси.

Напряжения при внецентренном растяжении-сжатии определяются по формуле (8.15)

Рисунок 8.9 – Пример внецентренного приложения нагрузки

1. Определим моменты инерции поперечного сечения

153