
- •1.4.2 Дифференциальные зависимости между поперечной силой,
- •изгибающим моментом и интенсивностью распределенной нагрузки.
- •1. 6 Понятие о деформациях и перемещения
- •1.7 Основные принципы сопротивления материалов
- •При действии на относительно жесткое тело нескольких сил, результат действия одной части этих сил не зависит от результата действия остальных сил. Рассмотрим балку, нагруженную силами F1, F2 и F3 (рисунок 1.14).
- •1.7.3 Принцип Сен-Венана
- •(II теория прочности)
- •3.7.3 Критерий наибольших касательных напряжений
- •(III теория прочности)
- •3.7.4 Критерий наибольшей удельной потенциальной энергии
- •формоизменения (IV теория прочности)
- •3.7.5 Критерий прочности Мора (V теория прочности)
- •7.2 Выбор рациональной формы сечения при изгибе
- •8 СЛОЖНОЕ СОПРОТИВЛЕНИЕ
- •8.1 Косой изгиб
- •8.2 Внецентренное растяжение (сжатие)
- •8.3 Совместное действие изгиба и кручения
- •10.4 Учет симметрии при раскрытии статической неопределимости
- •Решение
- •Степень статической неопределимости

s IV |
= |
1 |
s |
-s |
2 |
+ s |
|
-s |
2 |
+ s |
-s |
2 |
] . |
(3.58) |
|
2 ) |
2 |
3 ) |
1 ) |
||||||||||
экв |
|
2 |
[( 1 |
|
( |
|
( 3 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Условие прочности в соответствии с (3.50) имеет следующий вид:
s IV |
= |
1 |
s |
-s |
2 |
+ s |
|
-s |
2 |
+ s |
|
-s |
2 |
] |
£ s |
.] |
(3.59) |
|
2 ) |
2 |
3 ) |
3 |
1 ) |
||||||||||||
экв |
|
2 |
[( 1 |
|
( |
|
( |
|
[ |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Последнее условие прочности хорошо согласуется с результатами испыта-
ния изотропных материалов, поэтому оно широко применяется при расчете де-
талей из металлических материалов.
3.7.5 Критерий прочности Мора (V теория прочности)
Критерий прочности Мора основан на предположении, что прочность ма-
териалов в общем случае напряженного состояния зависит главным образом от величины и знака наибольшего σ1 и наименьшего σ3 главных напряжений и по-
зволяет учесть различие в свойствах материалов при растяжении и сжатии. Его можно получить путем модификации теории наибольших касательных напря-
жений в соответствии с уравнением:
s III |
= s |
1 |
- |
|
s |
3 |
£ s |
] |
p |
. |
|
|
|
(3.60) |
|||||||
экв |
|
|
|
|
|
|
k |
[ |
|
|
|
|
|
|
|||||||
При одноосном сжатии в предельном случае σ1=0, σ3= – σтсж |
|
||||||||||||||||||||
s III |
= |
0 |
- |
|
|
s |
Тсж ) |
£ s |
] |
p |
, |
(3.61) |
|||||||||
экв |
|
|
|
|
k ( |
|
|
[ |
|
|
|
||||||||||
откуда определяется коэффициент k |
|
||||||||||||||||||||
k = |
sТр |
|
» |
[s ]р |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
, |
|
|
|
|
|
(3.62) |
||||||||||
sТсж |
|
[s ]сж |
|
|
|
|
|
||||||||||||||
для пластичных материалов, или |
|
||||||||||||||||||||
k = |
s Вр |
|
|
» |
|
[s ]р |
|
|
|
|
|
|
|
|
|
|
(3.63) |
||||
s Всж |
|
|
[s ]сж |
|
|
|
|
|
|
|
|
|
|||||||||
для хрупких материалов.
Условие прочности по теории Мора имеет следующий вид:
s III |
= s |
1 |
- |
s |
£ s |
p |
. |
(3.64) |
экв |
|
|
k 3 |
[ |
] |
|
77
Достоинства критерия Мора бесспорны, так как он основан на опытных данных. Основные недостатки: необходимость проведения ряда опытов с пло-
ским и объемным напряженным состоянием; также как и третий критерий не учитывает влияние второго главного напряжения.
3.7.6 Замечания о выборе критерия прочности
Обзор многочисленных критериев предельных состояний показывает, что совершенных критериев еще нет. Каждый из существующих критериев спра-
ведлив только в определенных условиях и для определенных материалов. Рас-
смотренными выше критериями можно пользоваться только при напряженных состояниях с главными напряжениями разных знаков. Возможность примене-
ния этих критериев в случаях трехосного растяжения или сжатия требует - до полнительной экспериментальной проверки.
При выборе критерия прочности в случае плоского напряженного -со стояния и объемного напряженного состояния с главными напряжениями раз-
ных знаков надо учитывать свойства материала. Если материал пластичен и одинаково работает на растяжение и сжатие, то следует пользоваться критерием наибольшей энергии формоизменения или критерием максималь-
ных касательных напряжений. Если пластичный материал неодинаково сопро-
тивляется растяжению и сжатию, то следует пользоваться критерием Мора.
Расчет хрупких материалов при указанных напряженных состояниях следует производить по критерию Мора.
4СДВИГ (СРЕЗ)
4.1Напряжения при сдвиге
Сдвигом называется такой вид нагружения бруса, при котором в его по-
перечных сечениях из шести составляющих главного вектора и главного - мо мента внутренних сил, от нуля отличается только поперечная сила. Сдвиг, как вид нагружения бруса, встречается редко, чаще всего он сопровождается изги-
78
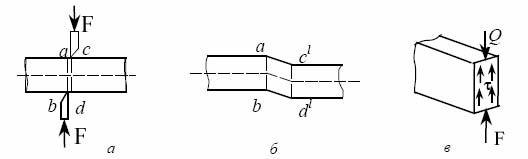
бающими моментами. Однако, в некоторых случаях, например в заклепочных и сварных соединениях, при раскройных работах, имеет место близкое к сдвигу нагружение бруса (рисунок 4.1).
Рисунок 4.1 - Деформация сдвига
Деформацию сдвига с достаточной степенью приближения можно полу-
чить практически, если на брус с противоположных сторон будут действовать две равные силы, перпендикулярные к оси бруса и направленные в противопо-
ложные стороны. Примером такого действия сил может быть резка ножницами металлических листов (рисунок 4.1). Поперечная сила в сечении бруса на уча-
стке действия сосредоточенных сил определяется методом сечений и составля-
ет Q=F (рисунок 4.1).
Если расстояние между сосредоточенными силами мало, то можно пре-
небречь величиной изгибающего момента. При этом распределение касатель-
ных напряжений по сечению неравномерно. Тем не менее, как показывают ис-
следования, распределение касательных напряжений весьма близко к равно-
мерному, и поэтому в первом приближении с целью упрощения расчетов заме-
няется равномерным законом распределения. Тогда на основании интегральных уравнений равновесия, получаем связь поперечной силы с касательным напря-
жением:
Q = òtdA ; t = Сonst ; Q = tA.
A
Таким образом, касательные напряжения при сдвиге (срезе) определяются из следующего уравнения:
79
t = |
Q |
(4.1) |
|
, |
|||
|
A
где Q – поперечная сила в сечении, А- площадь среза.
4.2 Анализ напряженного состояния при сдвиге
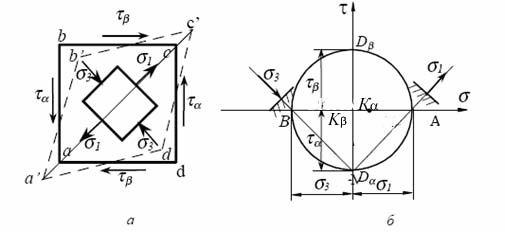
При сдвиге в поперечных сечениях возникают только касательныена пряжения. Такой случай напряженного состояния, когда по граням выделенно-
го элемента действуют только касательные напряжения (рисунок 4.2) называ-
ется чистым сдвигом.
Рисунок 4.2 - Определение главных напряжений при чистом сдвиге
Найдем величину и направление главных напряжений при чистом сдвиге.
Для этого воспользуемся построением круга напряжений(рисунок 4.2,б). По-
скольку в данном случае
sa = sb = 0 ; ta = -t ; tb = t ,
то построив круг напряжений, находим, что
s1 = -s3 = t ,
аглавные площадки наклонены к граням элемента под углом45о. Напряжения по третьей главной площадке, совпадающей с ненагруженной фасадной гранью
элемента s2 = 0 .
80
Рассмотрим деформацию элементаabcd (рисунок 4.2,а). Поскольку по граням элемента нет нормальных напряжений, то вдоль граней нет и удлине-
ний. В то же время диагональ ac, совпадающая с направлением σ1, удлиняется,
а диагональ bd , совпадающая с направлением сжимающего напряжения 3,σ
укорачивается. В результате квадрат abcd превращается в ромб a´b´c´d´. Таким образом, деформация чистого сдвига характеризуется изменением первона-
чально прямых углов.
4.3 Закон Гука при сдвиге
Более наглядное представление о деформации элемента можно получить,
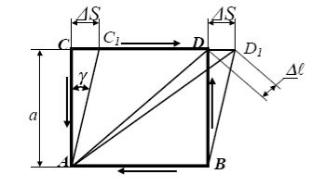
закрепив дну из граней (рисунок 4.3).
Рисунок 4.3 - Деформация сдвига
Если грань АВ закрепить неподвижно, то под действием касательных на-
пряжений грань DС сдвигается параллельно АВ на некоторую величину
DD1=CC1=ΔS, называемую абсолютным сдвигом. Элемент АВСD перекосит-
ся, прямые углы изменятся на угол γ. Этот угол γ называется относительным
сдвигом или углом сдвига и является мерой искажения углов прямоугольного элемента. Поскольку рассматриваются деформации упругие, то этот угол будет весьма малым:
g = tgg = |
DS |
. |
(4.2) |
|
|
||
|
a |
|
|
Экспериментально можно показать, что между относительным сдвигом и касательными напряжениями, действующими по граням элемента, существует линейная связь, которая определяется законом Гука при сдвиге
81
t = Gg , |
g = |
t |
. |
(4.3) |
|
G
где G - коэффициент пропорциональности, который называется модулем упру-
гости второго рода или модулем сдвига и измеряется в Па, МПа.
4.4 Связь между тремя упругими константами
Установим связь между относительным сдвигом γ и касательным напряже-
нием τ. При перекосе элемента диагональ AD удлиняется на величину
Dl = DS ×Cos45o
e = |
Dl |
|
= |
DSCos45o |
Sin45 |
o |
= |
DS |
. |
(4.3) |
|
l |
a |
|
2a |
|
|||||||
|
|
|
|
|
|
|
|||||
Учитывая (4.2) получаем: |
|
|
|
|
|
|
|||||
e = |
g |
|
|
|
|
|
|
|
|
(4.3) |
|
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
С учетом закона Гука для чистого сдвига (4.3) имеем: |
|
||||||||||
e = |
t |
. |
|
|
|
|
|
|
(4.4) |
||
|
|
|
|
|
|
|
|||||
|
2G |
|
|
|
|
|
|
|
|
||
С другой стороны, относительное удлинение диагонали, вызванное дей-
ствием главных напряжений σ1=τ и σ2=-τ, можно найти из обобщенного зако-
на Гука
e = e1 |
= |
1 + m |
t . |
(4.5) |
||
|
|
|||||
|
|
|
Е |
|
||
Сравнивая (4.4) и (4.5), получаем зависимость |
|
|||||
G = |
|
E |
(4.6) |
|||
|
|
. |
|
|||
|
|
|
||||
2(1 + m)
При µ=0,25÷0,33 получим G=(0,375÷0,4)E. Формула (4.6) выражает связь между тремя упругими константами E,G, µ.
Подставляя в выражение закона Гука(4.3) касательные напряжения при сдвиге из (4.1) и относительный сдвиг из (4.2) получим:
82
Q |
= G |
DS |
, |
DS = |
Qa |
|
(4.7) |
A |
|
GA |
|||||
|
a |
|
|
||||
Формула (4.7) выражает закон Гука для абсолютного сдвига.
4.5Потенциальная энергия при сдвиге
Удельная потенциальная энергия деформации при чистом сдвиге опреде-
ляется из уравнения (3.29):
u = |
t |
2 |
; |
t = |
Q |
; u = |
dU |
. |
|
|
|
(4.8) |
|||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
dV |
|
|
|
|
|
|||||||||
|
2G |
|
|
A |
|
|
|
|
|
|
|
||||||
Потенциальная энергия деформацииU определится путем интегрирова- |
|||||||||||||||||
ния по объему: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
2 |
(z) |
|
|
2 |
(z) A(z) |
|
2 |
(4.9) |
||||
U = ò udV = ò |
Q |
dz ò dA = ò |
|
Q |
dz = ò |
Q |
(z) |
dz . |
|||||||||
|
|
|
|
2GA2 (z) |
|
|
|||||||||||
|
V |
|
|
l |
2GA A |
l |
|
l |
2GA(z) |
||||||||
Например, в брусе постоянного сечения при действии постоянной по длине поперечной силы, имеем
2 |
(4.10) |
||
U = |
Q |
l |
. |
|
|
||
|
2GA |
||
|
|
4.6 Проверка прочности при чистом сдвиге |
|
Анализ напряженного состояния показал, что для случая чистого сдвига |
|||
σ1=τ σ2=0 σ3=-τ. При подстановке этих значений главных напряжений в ус- |
|||
ловия прочности по второму,третьему и четвертому критерию прочности по-
лучаем значения допускаемого напряжения в пределах:
[τ] = (0,5÷0,8) [σ]
Условие прочности на сдвиг (срез) может быть записано в виде:
t = |
Qmax |
£ [t ] |
(4.11) |
max |
A |
|
|
|
|
||
83
Величина допускаемых напряжений на срез [τ] зависит от материала, ха-
рактера нагрузки и типа элементов конструкции.
4.7 Расчет на прочность болтовых и заклепочных соединений
Рассмотрим основы практических расчетов на срез болтовых и заклепоч-
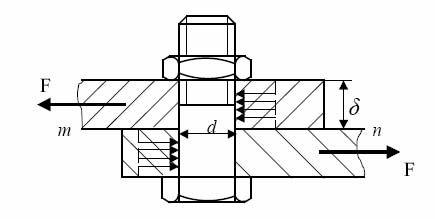
ных соединений. Более подробно эти вопросы освещаются в курсах деталей машин и конструкций. На рисунке 4.4 показано болтовое соединение двух лис-
тов. Соединение разрушается в результате среза болта по линии соприкоснове-
ния листов.
Рисунок 4.4 - Болтовое соединение
Учитывая большие трудности, связанные с определением действительно-
го напряженного состояния материала болта в зоне разрушения, для упрощения задачи принимаем, что по плоскостям среза действуют только касательные на-
пряжения, которые распределяются по поверхности среза равномерно.
t = |
Q |
(4.12) |
|
, |
|||
|
A
где F - сила, действующая на соединение.
Следует отметить, что силы F, приложенные к болту стремятся также изогнуть его. Однако изгибающий момент мал и вызванными им нормальными напряжениями можно пренебречь.
Приняв указанные допущения, получим условие прочности болтового со-
единения на срез:
84
tmax |
= |
Q |
= |
4F |
£ [t ], |
tmax |
= |
Q |
= |
4F |
£ [t ] |
(4.13) |
|
pd 2 |
|
npd 2 |
|
||||||||
|
|
A |
|
|
|
A |
|
|
||||
где А=πd2/4 - площадь поперечного сечения болта диаметром d, [τ]≈(0.5÷0.8)[σ] - допускаемое касательное напряжение. При многосрезном болтовом соедине-
нии в формуле (4.13) следует учитывать общее число срезов болтов n.
Кроме расчета на срез болтовые соединения рассчитывают также н
смятие. Проверяют напряжения смятия по площади соприкосновения соеди-
няемых листов и болтов. С целью приближенного расчета истинная эпюра рас-
пределения сжимающих напряжений смятия заменяется приближенной равно-
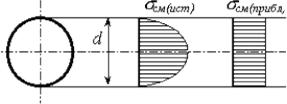
мерной эпюрой (рисунок 4.5). За площадь смятия болта принимается площадь диаметрального сечения равная Асм= dδ, где δ - толщина соединяемых листов.
Рисунок 4.5 - Распределение напряжений смятия
Условие прочности на смятие имеет следующие вид:
s |
|
= |
F |
= |
F |
£ |
[s ] |
, |
(4.14) |
см |
|
|
|
||||||
|
|
Aсм |
|
ndd |
см |
|
|
||
|
|
|
|
|
|
|
|||
[σсм]≈(0.5÷0.6)[σ] - допускаемое напряжение на смятие.
Кроме расчета на срез и смятие составляют такжеусловие прочности
листа на разрыв:
s = F |
= |
F |
£ |
[s ] |
(4.15) |
|
|
|
|
|
|
|
|
|
A |
|
d (b - n d ) |
|
|
|
|
min |
|
1 |
|
|
|
- площадь сечения листа по ряду, болтов в направлении, перпендику-
лярном линии действия силыF; n1 – число болтов в этом сечении; b - ширина листа (рисунок 4.5).
4.8 Расчет сварных соединений
85
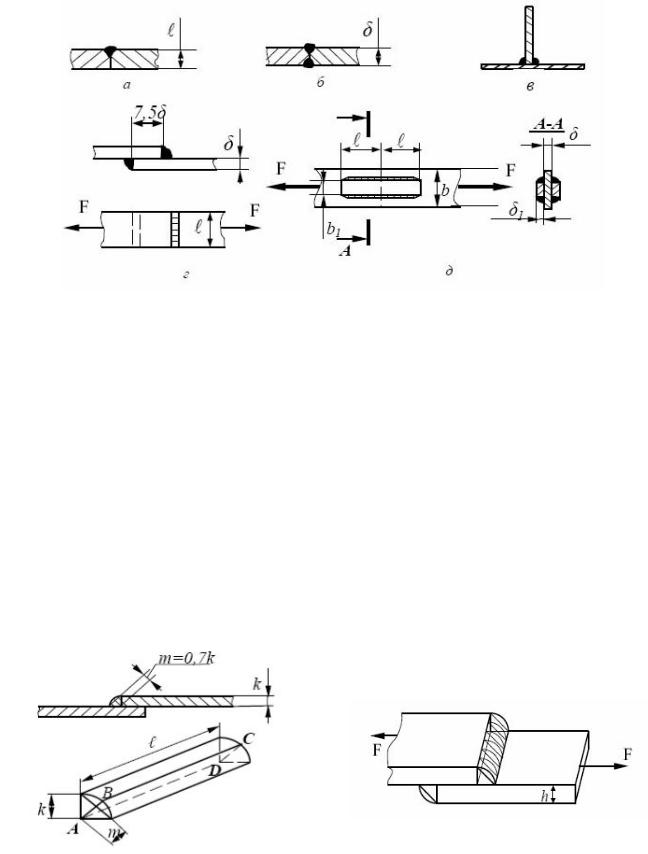
Сварные соединения рассчитывают на срез. Наиболее распространены соединения в стык и с помощью угловых и валиковых швов. Соединения в стык применяют, когда соединяемые листы находятся в одной плоскости(ри-
сунок 4. 6,а,б). При толщине листов δ = 8÷20 мм сварку производят с односто-
ронней V-образной разделкой шва (рисунок 4.6,а), при толщине δ > 20мм - с
двусторонней Х-образной разделкой шва (рисунок 4.6,б).
Рисунок 4.6 - Сварные соединения
Соединения с помощью угловых швов производят, когда листы парал-
лельны или перпендикулярны. На рисунке 4.6,г показано соединение листов в нахлестку лобовыми швами (перпендикулярными действующему усилию), а на
рисунке 4.6,д соединение с накладками приваренными фланговыми швами
(параллельными действующему усилию).
Если не учитывать наплывы, то в разрезе угловой шов имеет форму рав-
нобедренного прямоугольного треугольника(рисунок 4.7,а). Разрушение шва
будет происходить по его минимальному сечениюABCD, высота которого a = d × Cos45o » 0,7d . Расчетная площадь шва Aэ = a × l = 0,7d ×l , где l- длина
шва.
а)
б)
86
Рисунок 4.7 - К расчету сварных швов
Сварные соединения, как болтовые и заклепочные условно рассчитывают в предположении равномерности распределения напряжений по сечению шва.
Для соединения внахлестку в расчет вводят оба шва(рисунок 4.7,б) –
верхний и нижний. Предположив, что работают оба шва с общей площадью
Aэ = 2a × lТ = 2 × 0,7d × l = 1,4d ×lT ,
где lT - расчетная длина торцевого шва, которая принимается за счет возможно-
го непровара шва в начале и в конце lT = (l-10 мм), где |
l - действительная |
|||||||
длина шва. Таким образом, |
условие прочности на срез |
сварного соединения |
||||||
имеет вид: |
|
|
|
|
|
|
||
t = |
F |
= |
F |
= |
|
F |
£ [t э ]. |
|
|
1,4d × lT |
|
|
|
||||
|
Aэ |
1,4d (l -10) |
|
|
||||
5 ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ
Как ранее отмечалось, основным объектом, изучаемым в курсе “Сопро-
тивление материалов”, является брус. До сих пор в качестве геометрической характеристики сечения использовалась площадь поперечного сечения. Однако,
материал с одинаковыми свойствами и одинаковыми площадями поперечного сечения по-разному сопротивляется деформации в зависимости от очертания оси, формы поперечных сечений и их расположения. Поэтому, отвлекаясь от
87
физических свойств изучаемого объекта, рассмотрим геометрические характе-
ристики его поперечных сечений. К ним относятся площади поперечных сече-
ний, статические моменты площади, моменты инерции, радиусы инерции, мо-
менты сопротивления.
5.1 Статические моменты площади. Центр тяжести площади фигуры
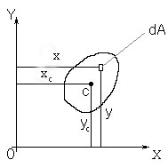
Рассмотрим произвольное поперечное сечение бруса, связанное с коор-
динатными осями OY и OX. Выделим элемент площади dA с координатами y, x
(рисунок 5.1). По аналогии с выражением для момента площади
Рисунок 5.1- Определение положение центра тяжести
dSx=ydA dSy=xdA
Просуммировав эти произведения по всей площади, получим:
S x = ò ydA , S y |
= ò xdA, |
(5.1) |
A |
A |
|
где Sx, Sy - статические моменты площади фигуры, относительно осей Y, X
(размерность м3, см3).
Статический момент площадиинтеграл произведений элементар-
ных площадок на расстояние до оси. Статический момент может быть поло-
жительным, отрицательным и равным нулю.
Если координаты центра тяжести фигуры yc, xc , то
Sx=A×yc ; Sy=Axc
Откуда координаты центра тяжести фигуры
88
X |
|
= |
S y |
Y |
= |
S |
(5.2) |
|
c |
|
|
x |
|
||||
|
|
|
|
|||||
|
|
A |
c |
A |
||||
|
|
|
|
|
||||
Для вычисления статических моментов сложной фигуры ее разбивают на простые, для каждой из которых известна площадь(Аi) и положение центра тя-
жести (yi , xi). Статический момент площади всей фигуры относительно данной оси определяется как сумма статических моментов каждой части:
n
Sx = A1 y1 + A2 y2 + K+ An yn = å Ai yi
i=1
n
S y = A1 x1 + A2 x2 + K+ An xn = å Ai xi
i=1
Координаты центра тяжести сложной фигуры определяются :
n |
n |
(5.3) |
yc = |
Sx |
= |
å Ai yi |
; |
X c |
= |
S у |
= |
å Ai xi |
i=1 |
i=1 |
||||||||
|
n |
|
n |
||||||
|
A å Ai |
|
|
|
A å Ai |
||||
|
|
|
i=1 |
|
|
|
|
|
i=1 |
5.2 Моменты инерции плоских фигур
Осевым или экваториальным моментом инерции площади фигуры называется интеграл произведений элементарных площадок на квадрат расстояния до оси.
Так, момент инерции произвольной фигуры относительно осейY,Х рав-
ны:
J y = ò x2 dA, |
(5.4) |
I x = ò y 2 dA. |
|
A |
A |
Полярным моментом инерции площади фигуры относительно дан-
ной точки (полюса О) называется интеграл произведений элементарных площадок на квадрат расстояния от полюса.
J p = ò r 2 dA |
(5.5) |
A |
|
Учитывая, что r2=y2+x2 (рисунок 5. 2), то из уравнения (5.5) |
|
J p = ò( y 2 + x2 )dA = J x + J y , Jp=Jx+Jy . |
(5.6) |
A |
|
89

Величины осевых и полярных моментов инерции всегда положительны и имеют размерность м4, см4.
Рисунок 5.2 - Элемент в системе координат
Центробежным моментом инерции называется интеграл произведе-
ний элементарных площадок на их расстояние от координатных осейX,Y.
В зависимости от положения осей центробежный момент инерции может быть
положительным, отрицательным и равным нулю. Оси, относительно которых
J xy = ò xydA. |
(5.7) |
A |
|
центробежный момент инерции равен нулю, называются главными осями инерции.
5.3Моменты инерции простейших фигур
5.3.1Момент инерции прямоугольника
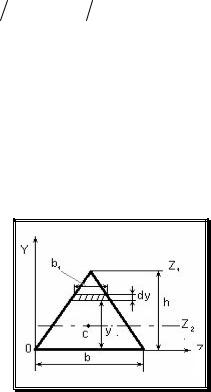
Выделим элементарную площадку в виде узкого прямоугольника, парал-
лельного оси X (рисунок 5.3). Площадь элементарной площадки dA=b×dy,
Pисунок 5.3 - Моменты инерции прямоугольного сечения
90
|
|
2 |
|
|
+h / 2 |
2 |
|
|
|
y3 |
|
+h / 2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
J x = ò y |
|
dA = b ò y |
|
dy |
= b |
|
|
|
|
|
|
= |
|
|
|
||||
|
|
3 |
|
|
-h / 2 |
|
|
|
|||||||||||
|
A |
|
|
|
-h / 2 |
|
|
|
|
|
|
|
|
|
|
||||
é(h 2)3 |
(- h 2)3 ù |
|
éh3 |
|
|
h3 ù |
|
bh3 |
|||||||||||
= bê |
|
|
|
- |
|
|
|
ú |
= bê |
|
|
+ |
|
ú |
= |
|
|||
3 |
|
3 |
|
|
|
|
24 |
12 |
|||||||||||
ë |
|
|
|
û |
|
ë24 |
|
û |
|
||||||||||
Таким образом:
I x = |
bh3 |
I y |
= |
hb3 |
||
|
, |
|
||||
12 |
12 |
|||||
|
|
|
|
|||
5.3.2 Момент инерции треугольника (рисунок 5.4)
х
Pисунок 5.4 - Моменты инерции треугольного сечения
dA=b1dy; |
|
|
|
|
b = |
b |
|
(h - y) |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
1 |
|
h |
|
|
|
|
|
|
|
|
|
|
J x = ò y 2 dA = b ò y 2 |
|
|
- y)dy = bh |
3 |
|
|
|
|||||||||||||
(h |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
h |
0 |
|
|
|
|
|
|
|
12 |
|
|
|
||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
I x = |
|
bh3 |
; |
I x1 |
= |
|
bh3 |
|
; I x = |
bh3 |
|
; |
I x2 |
= |
bh3 |
|||||
12 |
|
|
4 |
|
12 |
|
36 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
5.3.4 Момент инерции круга
(5.8)
(5.9)
Определим полярный момент инерции круга относительно его центра.
Выделим элементарную площадку в виде кольца толщиной dr (рисунок 5.5):
|
r |
pr |
4 |
|
pd |
4 |
dA=2prdr. J p = ò r2dA = 2p ò r3dr = |
|
= |
|
|||
2 |
|
|
||||
A |
0 |
32 |
||||
|
|
|
|
|
||
91

Pисунок 5.5- Моменты инерции круга
Учитывая, что Jp=Jy+Jx , и в силу симметрии
Jy=Jx ; Jy=Jx=pd4/64
dA=2prdr. |
J p = ò r |
2 dA = 2p ò r 3 dr = pr |
4 |
= pd |
4 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
0 |
2 |
|
|
32 |
|
|||
|
|
|
|
|
4 |
|
|
|
4 |
|
|
|
|
|
(5.10) |
||
I |
|
= I |
pd |
I |
|
|
|
pd |
|
|
|
|
|
|
|
||
|
, |
|
= |
. |
|
|
|
|
|
|
|||||||
|
|
|
p |
|
|
|
|
|
|
|
|||||||
x |
y 64 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
32 |
|
|
|
|
|
|
|
|||||
Момент инерции кольца можно найти как разность моментов инерции двух кругов
I p = |
p (D |
4 |
- d |
4 |
); |
I x = I y |
= |
p (D |
4 |
- d |
4 |
) |
(5.11) |
|
|
32 |
|
|
64 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
При вычислении моментов инерции сложных сечений последние разбива-
ют на простые фигуры, моменты инерции которых известны.
5.3.5 Момент инерции сложной фигуры
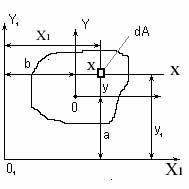
Pисунок 5.6 - Сложное сечение
Момент инерции сложной фигуры равен сумме моментов инерции ее со-
ставных частей (рисунок 5.6).
Jx= JxI+ JxII+ JxIII
Если в сечении есть отверстие, то его считают частью фигуры с отрица-
тельной площадью.
5.4 |
Моменты инерции относительно параллельных осей |
||
Пусть |
известны |
моменты |
инерции фигуры относительно центральных |
осей X,Y : |
|
|
|
J x = ò y2 dA; J y |
= ò x2 dA; |
J xy = ò xydA |
|
A |
|
A |
A |
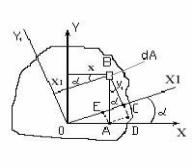
Необходимо определить моменты инерции относительно осей,
параллельных центральным (рисунок 5.7).
Рисунок 5.7- К определению моментов инерции относительно параллельных осей
J |
x |
= |
ò |
y 2dA; J |
y |
|
= |
ò |
x 2dA; |
J |
x y |
= |
ò |
x y dA |
|
|
1 |
|
|
1 |
|
1 |
1 1 |
||||||
|
1 |
|
A |
|
1 |
|
A |
|
|
1 |
A |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
где |
|
x1=x+b; |
|
y1=y+a. |
Тогда: |
|
|
|||||||
I x1 = ò ( y + a)2 dA = ò y2 dA + a2 ò dA + 2a ò ydA
A A A A
93
I y1 = ò (x + b)2 dA = ò x2 dA + b2 ò dA + 2bò xdA
A A A A
I x1 y1 = ò ( y + a)(x + b)dA = ò xydA + abò dA + a ò xdA+bò ydA
A A A A A
Так как ò xdA=Sy; ò ydA=Sx равны нулю как статические моменты инер-
A A
ции относительно центральных осей, то формулы моментов инерции, относи-
тельно осей, параллельным данным принимают вид:
Jx1=Jx+a2A, Jy1=Jy+b2A, Ix1y1=Jxy+abA. (5.12)
Следует отметить, что координаты a,b , входящие в формулу (5.12), необ-
ходимо подставлять с учетом знака. Из этих формул следует, что из всех мо-
ментов инерции относительно ряда параллельных осей моменты инерции отно-
сительно центральных осей будут наименьшими.
5.5 Зависимость между моментами инерции при повороте осей
Пусть известны моменты инерции произвольной фигуры, относительно координатных осей
Jx= ò y2dA ; |
Jy= ò x2dA ; |
Jyz= ò xydA . |
|
A |
|
A |
A |
|
|
|
|
|
|
|
|
Повернем осиисунокX Y на угол a протинерв часовой стрелки, считая такое Р 5.8 - Моменты ции при повороте осей
направление положительным (рисунок 5.8). Найдем
Jx1= ò y12dA ; Jy1= ò x12dA ; |
Jx1y1= ò x1y1 dA ; |
|
A |
A |
A |
94

Выразим координаты произвольной элементарной площадки dA в новых осях y1,x1 через координаты y,x:
x1=OC=OE+AD=x×cosa+y× sina
y1=BC=BD - EA=y×cosa - x×sina
П
Подставляя значения y1, x1 в уравнения для Jx1, Jy1 получим:
J x = ò ( yCosa - xSina)2 dA = |
|
||
1 |
|
|
|
A |
|
|
|
= Cosa 2 |
ò y2 dA + Sin2a ò x2 dA - 2Sina ×Cosa ò xy d A = |
||
|
A |
A |
A |
= Cosa 2 |
ò y2 dA + Sin2a ò x2 dA - Sin2a ò xy d A = |
||
|
A |
A |
A |
= J x Cosa 2 |
+ J y Sin2a - J xy Sin2a |
|
|
Производя аналогичные вычисления получим:
Jx1=Jxcos2a+Jysin2a-Jxysin2a
Jy1=Jycos2a+Jxsin2a-Jxysin2a,
Jx1y1=Jxycos2a- 1 (Jy-Jx)×sin2a .
2
Складывая почленно уравнения (5.13) получим:
(5.13)
(5.14)
Jx1+Jy1=Jx+Jy=Jp=const. |
(5.15) |
|
Анализ уравнений (5.14)(5.15) показывает, что при повороте прямоуголь-
ных осей на угол a=900 получаем
Jx1=Jy ; Jy1=Jx ; Jx1y1=-Jxy.
5.6 Определение направления главных осей
Главные моменты инерции
Согласно принятому ранее определению главные осиэто оси, относи-
тельно которых центробежный момент инерции равен нулю.
Обозначим главные оси U,V:
95

Juv=0
Повернем произвольную систему на угол a0, при котором Jx1y1=Juv=0;
Тогда
|
2 |
|
(I y |
- I x ) |
|
|
I x y = I xyCos ao |
- |
|
|
Sin2ao |
= 0 , |
|
|
2 |
|||||
1 |
1 |
|
|
|
|
|
|
|
|
|
|
||
откуда
tg2ao |
= |
2I xy |
(5.16) |
|
I y |
-I x |
|
||
|
|
|
||
Полученное значение a0 позволяет определить положение главных осей. Отри-
цательные значения угла a0 откладывают по ходу часовой стрелки.
Значения главных моментов инерции можно получить из общих формул
(5.13) при a=a0: |
|
Ju=Jxcos2a0+Jysin2a0 - Jxysin2a0 |
(5.17) |
Jv=Jxsin2a0+Jycos2a0 - Jxysin2a0
Составим выражение суммы Ju+Jv (из 5.17) получим
Ju+Jv = Jx+Jy
Составив выражение разности Jx и JY и выполнив преобразования, полу-
чим
|
|
|
J x |
+ J y |
|
|
1 |
|
|
|
|
(5.18) |
J u |
= |
|
± |
|
|
(J x - J y )2 |
+ 4J xy2 |
|||||
|
|
2 |
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
J x |
+ J y |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|||
J v |
= |
|
|
|
m |
|
|
|
(J z - J y ) |
|
+ 4J xy |
|
|
|
2 |
|
2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
Если вместо произвольной начальной системы принять главные оси, то форму
Jx1=Jucos2a+Jvsin2a , |
(5.19) |
||||
|
|
|
|
|
|
Jy1=Jusin2a+Jvcos2a , |
|
||||
I x y |
= |
Iu - Iv |
Sin2a . |
(5.20) |
|
|
|||||
|
|
||||
1 |
1 |
2 |
|
|
|
96

Главные моменты инерции обладают свойством экстремальности. В этом
можно убедиться, исследовав функции Jx1 на экстремум.
dI x 1 |
= -2I x y = 0 . |
||
da |
|||
1 |
1 |
||
|
|||
Отсюда следует, что производная dIx1/da=0, когда Jx1y1=0, а это значит,
что экстремальные значения имеют моменты инерции относительно главных
осей.
dI x 1 |
= -2I x y = 0 . |
||
da |
|||
1 |
1 |
||
|
|||
5.7 Радиусы инерции
Момент инерции фигуры можно представить в виде произведения пло-
щади фигуры на квадрат некоторой величины, называемой радиусом инерции
:
I x = ò y 2 dA = A ×ix2 .
A
где ix - радиус инерции относительно оси X. Отсюда
i |
|
|
= |
|
J |
x |
|
, |
аналогично i |
|
= |
J y |
. |
(5.21) |
|||||||||
x |
|
|
|
|
|
|
y |
A |
|
||||||||||||||
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
||||||||
Главным осям инерции соответствуют главные радиусы инерции |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
. |
|
|
|
|
|
|||
|
i |
u |
= |
|
|
|
Ju |
|
|
i |
|
J v |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
A |
v |
|
|
A |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
5.8 Моменты сопротивления
Осевым моментом сопротивления называется отношение момента инерции относительно данных осей к расстоянию до наиболее удаленной точки:
97
Wx |
= |
I x |
, Wy |
= |
I y |
. |
(5.22) |
ymax |
xmax |
|
|||||
|
|
|
|
|
|
Практическое значение имеют моменты сопротивления относительно главных осей. Вычислим моменты сопротивления для простых фигур.
Прямоугольник:
Wx |
= |
I x |
|
= |
bh3 |
× 2 |
= |
|
bh2 |
, |
Wy |
= |
I y |
= |
hb3 × 2 |
= |
hb |
2 |
. |
||||||||||
|
|
12 × h |
|
|
6 |
|
xmax |
12 ×b |
6 |
|
|||||||||||||||||||
|
|
ymax |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Круг: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Wx |
= Wy |
= |
|
I |
x |
|
= |
pd |
4 ×2 |
|
= |
pd 3 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|||||||||
d / 2 |
|
|
64 ×d |
32 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Трубчатое сечение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Wx = Wy |
= |
I x |
|
= |
p (D4 - d 4 ) |
= |
pD3 |
(1 -a 4 ), |
|
|
|
|
|||||||||||||||||
d / 2 |
|
|
|
|
|
|
|||||||||||||||||||||||
г |
|
|
|
|
|
|
|
|
|
d / 2 |
|
|
|
|
32 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где a=d/D.
Полярный момент сопротивления это отношение полярного момента инерции к расстоянию от полюса до наиболее удаленной точки:
- для круглого сечения
|
Wp = |
I p |
= |
pd 4 × 2 |
= |
pd 3 |
||||
|
|
|
|
|
, |
|||||
|
rmax |
|
32 × d |
16 |
||||||
|
|
|
|
|
|
|
|
|||
- для трубчатого сечения |
|
|
||||||||
Wp |
= |
pD3 |
(1 -a 4 ) |
|
|
|
||||
|
|
|
|
|||||||
|
16 |
|
|
|
|
|
|
|
|
|
5.9 Моменты инерции сложных сечений
Моменты инерции сплошных сечений сложной формы, например, сечение ло-
паток компрессора или турбины двигателя, которые невозможно разбить на простейшие фигуры, вычисляются приближенным интегрированием. Заданное сечение разбивается на небольшие части линиями, параллельными одной из
98
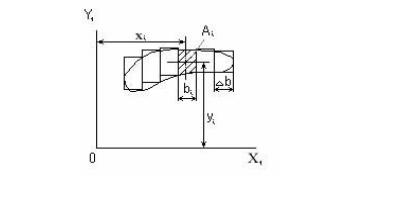
осей (рисунок 5.9). Отрезки криволинейного контура заменяются прямыми, па-
раллельными другой оси. В результате получают совокупность прямоугольни-
ков, приближенно составляющую данное сечение. Увеличение числа прямо-
угольников усложняет расчет, но увеличивает точность. Для упрощения расче-
та обычно берут ширину всех прямоугольников одинаковой.
Рисунок 5.9- Определение моментов инерции
Моменты инерции сечения вычисляются суммированием моментов инер-
ции составляющих прямоугольников относительно соответствующих осей. Со-
гласно правилам перехода к параллельным осям дляi-го прямоугольника име-
ем:
I |
|
= |
b h3 |
+ b h y2 |
|
I |
|
= |
h b3 |
+ h b x2 |
I |
|
|
= b h x |
y |
|
x |
i i |
; |
x |
i i |
x y |
|
i |
|||||||||
|
|
|
||||||||||||||
|
|
12 |
i i i |
|
|
|
12 |
i i i |
|
|
i i i |
|
||||
|
i |
|
|
|
|
i |
|
|
|
i |
i |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
6КРУЧЕНИЕ
6.1Внутренние силовые факторы при кручении
Кручением называется такой вид нагружения бруса, при котором из шес-
ти внутренних силовых факторов в поперечном сечении стержня возникает только крутящий момент. Кручение вызывается парами сосредоточенных и распределенных вдоль оси бруса сил, действующих в плоскостях, перпендику-
лярных этой оси. Брус, работающий на кручение, называется валом. Моменты,
99
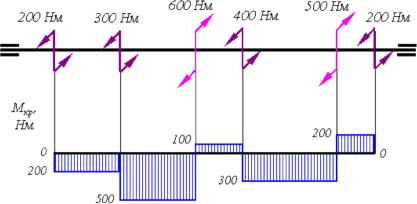
вызывающие деформацию кручения, называются крутящими моментами. Ве-
личина крутящего момента, действующего в каком-либо сечении вала, опреде-
ляется методом сечений (рисунок 6.1). Момент крутящий считается положи-
тельным, если при взгляде со стороны сечения он стремиться повернуть выде-
ленный элемент по часовой стрелке.
Рисунок 6.1 - Построение эпюр крутящих моментов
Величина крутящего момента может быть задана мощностью, переда-
ваемой на вал, например через шкив:
N = M k ×w , |
(6.1) |
где N - мощность, передаваемая на вал [Ватт]; ω [1/сек] – круговая частота вра-
щения вала; n - число оборотов вала [об/мин]. Если мощность задан в лошади-
ных силах, для перевода в систему Си следует помнить, что 1 л.с. = 736 Ватт.
6.2 Напряжения и деформации при кручении
Рассмотрим консольный стержень круглого поперечного сечения, нагру-
женный в концевом сечении моментом Mz. Под действием внешнего скручи-
вающего момента, приложенного на правом конце вала(рисунок 6.2) стержень будет закручиваться. При этом любое сечение стержня, оставаясь плоским, бу-
дет поворачиваться на некоторый на уголj (абсолютный угол закручивания).
Этот угол изменяется от нуля в заделке до максимального значения на правом конце вала. При этом образующая внешней цилиндрической поверхности вала
100
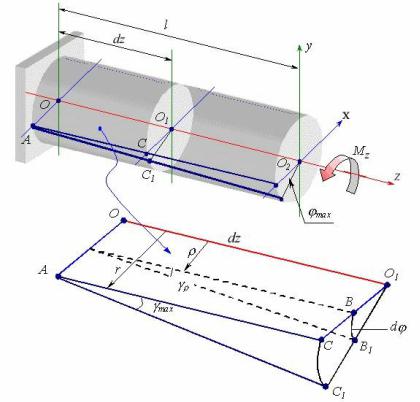
повернется на угол γ, называемый углом сдвига. Этот угол изменяется вдоль радиуса сечения от нуля на оси вала до γmax на внешней поверхности.
Рисунок 6.2 - Крутящие моменты и углы закручивания в стержне
Опыт показывает, что после закручивания бруса круглого сечения попе-
речные линии, нанесенные на его поверхности, остаются плоскими, а диаметры сечений и расстояния между ними не изменяются. При этом прямоугольная сетка превратится в сетку, состоящую из параллелограммов, что свидетельству-
ет о наличии касательных напряжений в поперечных сечениях бруса, а по зако-
ну парности касательных напряжений– и в продольных его сечениях, т.е. на-
пряженное состояние в точках скручиваемого стержня представляет собо
чистый сдвиг. На основании опыта вводятся следующие гипотезы:
-нормальные напряжения в поперечных сечениях отсутствуют(иначе изменялись бы расстояния между сечениями);
-поперечные сечения при кручении остаются плоскими;
-радиусы в поперечных сечениях остаются прямыми.
Выведем формулы для определения напряжений и перемещений стержня.
Статическая сторона задачи
101
Воспользуемся интегральным выражением, связывающим крутящий мо-
мент с касательным напряжением:
M к = òt × r × dA, |
(6.1) |
A |
|
Геометрическая сторона задачи
Выделим элемент стержня длиной dz. В результате кручения торцевые сечения этого элемента поворачиваются, причем точки B и C переходят в по-
ложения B1 и C1. С учетом указанных гипотез геометрическая картина дефор-
маций вала представлена на рисунке 6.2. Рассмотрим, вырезанный из вала кли-
новидный элемент длиной dz. Выразим длину дуги через угол сдвига g и эле-
ментарный угол закручивания dj:
СС1 = dz ×g , СС1 = r × dj , откуда |
r × dj = dz ×g , |
||
и угол сдвига |
|
||
g = |
dj |
r , |
(6.2) |
|
|
||
|
dz |
|
|
откуда следует, что угол сдвига изменяется по радиусу вала по линейному -за кону.
Обозначим относительный угол закручивания |
dj |
= Q, тогда |
|
||
|
dz |
|
g = Qr . |
(6.3) |
|
Физическая сторона задачи
Согласно закону Гука при сдвиге, имеем:
t = Gg , |
(6.4) |
Подставим выражение 6.3 в формулу 6.4:
t = GQr . |
(6.5) |
Полученное выражение подставляем в формулу 6.1:
M к = ò GQr2 dA = GQò r2 dA = GQJ ρ ,
A A
откуда относительный угол закручивания
102

Q = |
M |
(6.6) |
|
к |
, |
||
|
|
||
GJ r
где GJr - жесткость поперечного сечения при кручении.
Подставляя 6.6 в 6.5, получим формулу для касательных напряжений:
t = GQr = |
M |
к r |
(6.6) |
|
|
, |
|
|
|
J r
откуда следует, что касательные напряжения в сечении вала изменяются по ра-
диусу по линейному закону (рисунок 6.2).
а)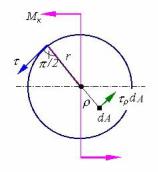 б)
б)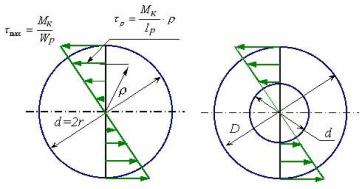
Рисунок 6.2 - Распределение касательных напряжений в сечении при кручении
Эпюры распределения касательных напряжений по радиусу для сплошно-
го и полого валов показаны на рисунке 6.2,б.
Наибольшее касательное напряжение
M r
tmax = J к , (6.7)
r
где r – радиус поперечного сечения стержня.
Таким образом, условие прочности при кручении:
tmax |
= |
|
M кmax |
£ [t ], |
(6.8) |
|||
Wr |
||||||||
|
|
|
|
|
|
|
||
где Wr |
= |
J r |
- полярный момент сопротивления. |
|
||||
|
|
|||||||
|
|
|
r |
|
|
|||
103
Для круглого сечения Wr |
= |
pd 4 |
× |
2 |
= |
pd 3 |
|
||||||||
|
|
|
|
|
. |
|
|||||||||
32 |
d |
16 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
Условие жесткости при кручении может быть записано через относитель- |
|||||||||||||||
ный угол закручивания |
|
|
|
|
|
|
|
|
|
|
|||||
Qmax |
= |
M кmax |
|
£ [Q ], |
|
|
|
|
|
|
|
|
|
(6.9) |
|
GJ r |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
либо через абсолютный угол закручивания |
|
||||||||||||||
j = ò Qdz = ò |
|
M к dz |
|
|
, jmax |
£ [j]. |
|
||||||||
|
|
, |
|
|
(6.10) |
||||||||||
|
|
|
|||||||||||||
l |
|
l |
|
GJ r |
|
|
|
|
|
|
|
|
|
|
|
6.3 Анализ напряженного состояния при кручении
Из анализа формулы касательных напряжений(6.3) следует, что напря-
жения в плоскости сечения вала неравномерно и в зависимости от радиуса из-
меняются по линейному закону от нуля в центре сечения до максимума на его поверхности (рисунок 6.2,б). В продольных сечениях, проходящих через ось вала, по закону парности касательных напряжений возникают такие же по ве-
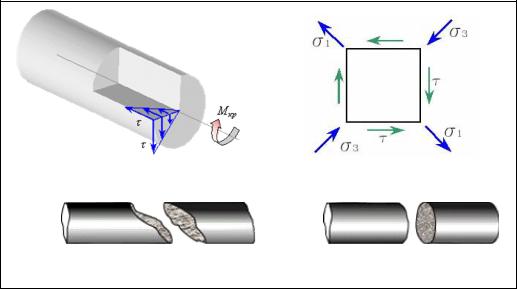
личине касательные напряжения (рисунок 6.3,а). В элементе материала, выде-
ленном из наружных слоев сечениями параллельными и перпендикулярными к образующим, действуют только касательные напряжения, т.е. возникает част-
ный случай плоского напряженного состояния, называемый чистым сдвигом.
а) |
б) |
в) |
г) |
104
Рисунок 6.3 - Напряженное состояние и характер разрушения при кручении
При чистом сдвиге по площадкам, наклоненным к оси бруса под углом
45°, действуют максимальные нормальные напряжения, равные по величине касательному напряжению в поперечном сечении. При этом одно из них будет растягивающим, а другое - сжимающим (рисунок 6.3,б). Во всех остальных на-
клонных площадках возникают одновременно касательные и нормальные -на пряжения. Однако наибольшие нормальные напряжения действуют на площад-
ках, проведенных под углом 45°, а наибольшие касательные напряжения - в по-
перечных сечениях.
При чистом сдвиге главные напряжения получаются равными по значе-
нию и противоположными по знаку (рисунок 6.3,б):
s1 = t , s3 = -t , |
s2 = 0 . |
(6.11) |
Площадки действия наибольших растягивающих напряжений располага-
ются на винтовой поверхности. Именно по этой поверхности и разрушаются при кручении образцы их хрупкого материала(рисунок 6.3,в), так кик хрупкие материалы слабее сопротивляются отрыву частиц, чем их сдвигу. Пластичные материалы, наоборот, обладают меньшим сопротивлением сдвигу, чем отрыву.
Поэтому образцы из таких материалов разрушаются при кручении по плоско-
сти поперечного сечения, где действуют наибольшие касательные напряжения
(рисунок 6.3,г).
6.4 Потенциальная энергия при кручении
Потенциальная энергия деформации при кручении определяется подобно тому, как это делалось при растяжении и сдвиге.
Удельная потенциальная энергия деформации при чистом сдвиге опреде-
ляется из уравнения (4.8)
u = |
t |
; t = |
M k r |
|
u = |
dU |
(6.12) |
|
|
|
; |
|
. |
||||
2G |
I p |
|
||||||
|
|
|
|
dV |
|
|||
105
Потенциальная энергия деформации U определится из уравнения (6.12)
путем интегрирования по объему:
U = |
òudV = ò |
M 2 |
(z) |
dzòr2 dA = ò |
Mk2 (z)I p |
dz =ò |
M 2 (z) |
(6.13) |
||||
k |
|
|
k |
dz . |
||||||||
|
|
2GIp2 |
2GIp (z) |
|||||||||
|
V |
|
l |
2GIp2 (z) A |
l |
l |
|
|||||
В брусе постоянной жесткости GIp при действии постоянного по длине |
||||||||||||
крутящего момента, имеем |
|
|
|
|
|
|||||||
U = |
|
|
M k2l |
|
|
|
|
|
|
|
(6.14) |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2GI p
6.5 Расчеты на прочность и жесткость при кручении
При кручении расчеты на прочность также делятся на проектировочные и поверочные. В основе расчетов лежит условие прочности
tmax £ [t ], |
(6.15) |
где τmax - максимальное касательное напряжение в брусе, определяемое по вы-
шеприведенным уравнениям в зависимости от формы сечения; [τ] - допускае-
мое касательное напряжение, равное части предельного напряжения для мате-
риала детали - предела прочности τв или предела текучести τт. Коэффициент за-
паса прочности устанавливается из тех же соображений, что и при растяжении.
Например, для вала полого круглого поперечного сечения, с внешним диамет-
ром D и внутренним диаметром d, имеем
M k |
= |
16M k |
£ [t ], |
(6.16) |
|
|
|
||
Wp |
pd 3 (1 -a 4 ) |
|
||
где α=d/D - коэффициент полости сечения.
Условие жесткости такого вала при кручении имеет следующий вид:
Qmax = M k |
= |
32M k £ |
[Q ], |
||
|
|
|
|
|
(6.17) |
|
GI p |
|
pd 3 (1 -a 4 ) |
|
|
где [θ] - допускаемый относительный угол закручивания.
6.6 Кручение стержней некруглого поперечного сечения
106
Опыт показывает, что при кручении бруса любого некруглого сечения его поперечные сечения искривляются (депланируют) (рисунок 6.4,а). Это обстоя-
тельство значительно усложняет задачу определения напряжений и деформа-
ций, так как не позволяет принять гипотезу плоских сечений. Поэтому задачи кручения брусьев некруглых сечений могут быть решены только методами тео-
рии упругости.
Наиболее распространенными являются стержни прямоугольного попе-
речного сечения. Решение задачи о кручении бруса прямоугольного сечения полученное в теории упругости, показывает, что касательные напряжения в контурных точках сечения возрастают от нулевых значений в углах к середи-
нам сторон по некоторым кривым (рисунок 6.4,б); в центре сечения напряжение равно нулю, а максимального значения напряжения достигают в серединах длинных сторон, причем
|
|
M |
max |
(6.18) |
|
tmax |
= |
к |
£ [t ]. |
|
|
|
|
|
|||
|
|
Wк |
|
||
Наибольшее напряжение на короткой стороне прямоугольника.
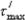

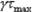 . (6.19)
. (6.19)
Угол закручивания определяется по формуле
jmax = |
M |
кmax l |
(6.20) |
|
|
|
, |
||
GJk |
||||
|
|
|||
где I x = b × h × b3, |
Wx |
= a × h ×b2 . |
||
В этих формулах b - длина короткой стороны; h - длинной сторону пря- |
||||
моугольника; α, β, γ - числовые коэффициенты, зависящие от соотношения сто-
рон h и b.
107
а) |
б) |
Рисунок 6.4 - Распределение касательных напряжений при кручении в стержне прямоугольного сечения
Значения этих коэффициентов приведены в таблице6.1. Характер изме-
нения касательных напряжений по различным направлениям внутри прямо-
угольного сечения показан на рисунок 6.4.
Таблица 7.1 - Значения коэффициентов α, β, γ для расчетов на прочность и жесткость стержней прямоугольного поперечного сечения
h/b |
1 |
1.5 |
1.75 |
2 |
3 |
4 |
6 |
8 |
10 |
¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
0.208 |
0.231 |
0.239 |
0.246 |
0.267 |
0.282 |
0.299 |
0.307 |
0.313 |
0.333 |
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
0.141 |
0.196 |
0.214 |
0.229 |
0.263 |
0.281 |
0.299 |
0.307 |
0.313 |
0.333 |
|
|
|
|
|
|
|
|
|
|
|
|
|
γ |
1.00 |
0.859 |
0.820 |
0.795 |
0.753 |
0.745 |
0.743 |
0.742 |
0.742 |
0.742 |
|
|
|
|
|
|
|
|
|
|
|
|
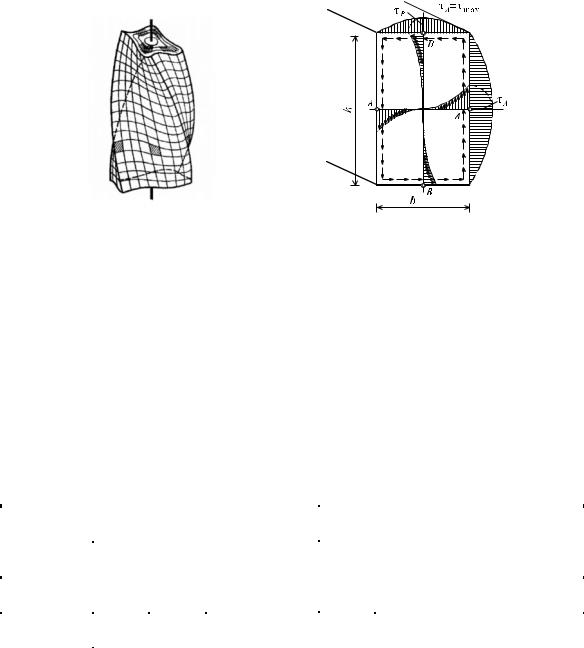
6.7 Расчет винтовых цилиндрических пружин
Определим напряжения и деформации при осевом растяжении и сжатии цилиндрической пружины, навитой из прутка круглого сечения диаметра d (ри-
сунок 6.5,а). Конструктивно пружины растяжения и сжатия отличаются оформ-
лением их концов, но концевые витки при расчетах пружин на прочность и же-
сткость во внимание не принимаются.
108
Цилиндрические пружины характеризуются средним диаметром виткаD,
числом витков n, углом подъема витковα и шагом пружиныh. Наибольшее распространение в технике имеют пружины с небольшим углом подъема вин-
товой линии (α<5°), называемые пружинами малого шага.
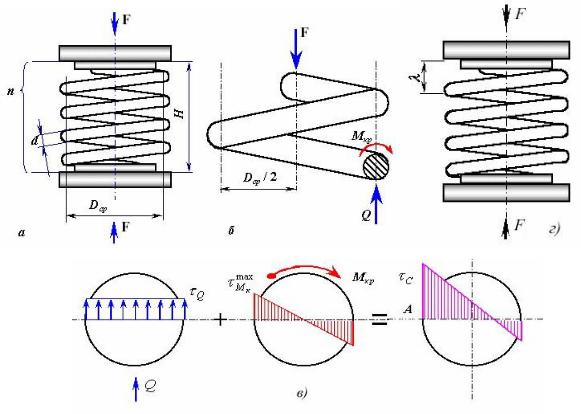
Рисунок 6.5 - К расчету винтовых цилиндрических пружин с малым шагом
В пружинах малого шага можно пренебречь подъемом витков и считать длину витка примерно равнойπD, а сам виток - расположенным в плоскости,
нормальной к оси пружины. Но в таком случае, сечение прутка пружины плос-
костью, содержащей ее ось, можно рассматривать как ее поперечное сечение.
Указанные допущения положены в основу приближенного расчета пружин.
Разделим пружину осевым сечением на две части и отбросим, одну из них. Из условия равновесия оставшейся части(рисунок 6.5, б) следует, что в поперечном сечении пружины возникает поперечная силаQ=F и крутящий моменту Мк=FD/2.
Касательные напряжения, вызванные кручением, достигают максимума в контурных точках сечения, а напряжения от поперечной силы можно в первом
109
приближении считать равномерно распределенными по плоскости сечения. В
точке А контура сечения суммарные касательные напряжения, как видно из ри-
сунка 6.5,в, достигают наибольшей величины.
t |
= t +t = |
M k + Q = |
8FD + |
4F , |
|||||
|
|
|
|
|
|
|
|
(6.21 |
|
max |
M Q |
W |
|
A |
|
pd 3 |
|
pd 2 |
|
|
|
k |
|
|
|
|
|||
или
|
|
|
8FD æ |
|
d ö |
(6.22) |
||
t |
max |
= |
|
ç1 |
+ |
|
÷. |
|
pd 3 |
|
|
||||||
|
|
è |
|
2D ø |
|
|||
Для большинства пружин отношениеd/2D - величина малая по сравне-
нию с единицей. Это говорит о том, что основным видом деформации для пру-
жин является кручение, а срезом можно пренебречь и вычислять напряжения в пружине по формуле
|
|
(6.23) |
|
tmax |
= |
8FD |
. |
|
|||
|
|
pd 3 |
|
Изменение продольных размеровλ (рисунок 6.5,г) удобно определить энергетическим методом, приравнивая работу А статически приложенной силы
F потенциальной энергии деформации U пружины. Работа внешних сил A=Fλ/2,
а потенциальная энергия накапливается, главным образом, за счет кручения прутка и поэтому может быть вычислена по формуле (6.14). Учитывая, что кру-
тящий Мк=FD/2 и момент инерции Ip=πd4/32 по длине прутка не изменяются, а
длина прутка l=πdn, получаем
2 |
|
|
|
|
3 |
(6.24) |
|||
U = |
M k l |
= |
4FD |
n |
. |
||||
|
Gd 4 |
|
|||||||
|
|
2GI p |
|
|
|||||
Приравнивая A и U, находим |
|||||||||
l = |
8pD |
3 |
n |
. |
|
(6.25) |
|||
|
|
|
|||||||
|
|
|
|
||||||
|
|
|
|
|
|
||||
|
|
Gd 4 |
|
|
|
|
|
|
|
110
Для пружин сжатия формула(6.25) справедлива лишь до полного обжа-
тия пружины, т. е. до соприкосновения ее витков. После полного обжатия пру-
жина начинает работать на осевое сжатие как прямой пустотелый брус.
При кручении, как и при растяжении, могут встретиться статически неоп-
ределимые задачи, для решения которых к уравнениям равновесия статики должны быть добавлены уравнения совместности перемещений.
6.8 Статически неопределимые задачи при кручении
Нетрудно показать, что метод решения указанных задач при кручении и при растяжении один и тот же. Рассмотрим для примера брус, заделанный обо-
ими концами в абсолютно жесткие стены (рисунок 6.6).
Отбросим заделки, заменив их действие неизвестными моментом M1 и M2.
Уравнение совместности деформаций получим из условия равенства нулю угла закручивания в правой заделке:
M 2 a + |
M1b = 0 |
, |
||
|
|
|
|
(6.25) |
GI p 2 |
|
GI p1 |
|
|
где Ip1=πd14/32, Ip2=πd24/32.
Крутящие моменты в сечениях бруса связаны следующим уравнением:
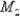

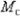

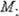 .
.
Решая совместно указанные уравнения относительно неизвестных момен-
тов, получим: |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
(M 2 + M 0 ) × a |
+ |
M1b |
= 0 , откуда |
(6.25) |
|||||||||
|
|
|||||||||||||
|
|
|
GI p1 |
|
||||||||||
|
GI p 2 |
|
|
|
|
|
|
|
|
|||||
|
M1 = |
|
|
|
M 0 |
× a |
|
|
; |
M |
2 = M 0 + M1 . |
|||
|
|
|
æ |
b |
|
|
|
a |
ö |
|||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
GI |
p 2 |
ç |
|
|
|
+ |
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
ç |
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
è GI p1 GI p 2 ø |
|
|
||||||||
111
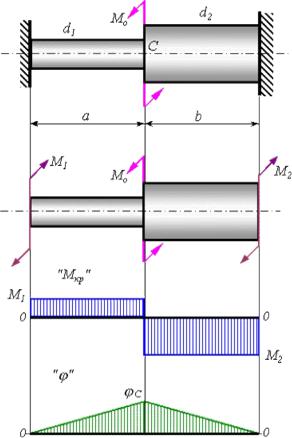
Рисунок 6.6 - К расчету статически неопределимых систем при кручении
Угол закручивания сечения C определяется из уравнения
jС |
= |
M |
2 a |
(6.26) |
|
|
|
, |
|||
GI p 2 |
|||||
|
|
|
|||
Эпюры крутящих моментов и углов закручивания представлены на -ри сунке 6.6.
7 ИЗГИБ ПРЯМЫХ СТЕРЖНЕЙ
При растяжении-сжатии, кручении прямых брусьев их оси, прямые до деформации, остаются прямыми и после деформации. В отличие от этих видов деформации, изгиб представляет собой такую деформацию, при которой проис-
112
ходит искривление оси прямого бруса. Осью бруса называется геометрическое место точек центров тяжестей поперечных сечений бруса, то есть сечений,
нормальных к оси бруса. Изгиб связан с возникновением в поперечных сечени-
ях бруса изгибающих моментов. Если из шести внутренних силовых факторов в сечении бруса отличным от нуля является только один изгибающий момент,
изгиб называется чистым. Если в поперечных сечениях бруса кроме изгибаю-
щего момента действует также поперечная силаизгиб называется попереч-
ным:
Брус, работающий на изгиб, называется балкой. Изгиб называется пло-
ским, если ось балки после деформации остается плоской линией. Плоскость расположения изогнутой оси балки называетсяплоскостью изгиба. Плоскость действия нагрузочных сил называетсясиловой плоскостью. Если силовая плоскость совпадает с одной из главных плоскостей инерции поперечного -се чения, изгиб называется прямым. (В противном случае имеет местокосой из-
гиб). Главная плоскость инерции поперечного сеченияэто плоскость, образо-
ванная одной из главных осей поперечного сечения с продольной осью бруса.
При плоском прямом изгибе плоскость изгиба и силовая плоскость совпадают.
Будем рассматривать плоский прямой изгиб призматических , бало имеющих, по крайней мере, одну ось симметрии, совпадающую с силовой плоскостью.
7.1 Нормальные напряжения при чистом изгибе
Из интегральных уравнений равновесия следует, что при изгибе нормаль-
ные напряжения зависят только от изгибающего момента, поэтому вывод фор-
мулы для вычисления σ можно производить применительно к чистому изгибу,
при котором во всех сечениях Q=0 и, в силу, Mx=const.
Экспериментальное изучение деформации изгиба позволяет заключить:
- на выпуклой стороне волокна растягиваются, а на вогнутой – сжимают-
ся; если на боковой стороне балки нанести прямоугольную сетку, то будет вид-
но, что переход от сжатых волокон к растянутым и наоборот происходитне
113
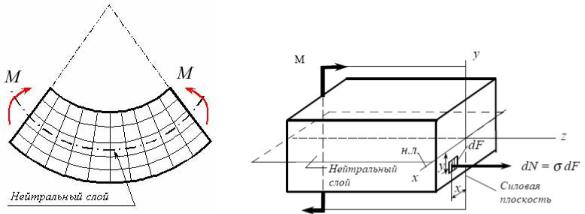
прерывно и что между ними естьнейтральный слой, то есть волокна, длина которых при изгибе не изменяется(рисунок 7.1); линия пересечения нейтраль-
ного слоя с плоскостью сечения называется нейтральной осью;
а) |
б) |
Рисунок 7.1- Изгиб в главной плоскости инерции.
Сечения поворачиваются вокруг нейтральной линии
- в силу эффекта Пуассона в растянутой зоне поперечные сечения сужа-
ются, а в сжатой – расширяются; - плоские поперечные сечения, нормальные к упругой линии балки до из-
гиба, остаются плоскими и нормальными к ней после изгиба(гипотеза плоских сечений Я. Бернулли);
- продольные волокна не оказывают давления друг на друга, а испытыва-
ют только осевое растяжение или сжатие, т.е. σy=0;
- картина деформаций по ширине сечения не изменяется, т.е. нормальные напряжения распределены по ширине сечения равномерно.
Для определения напряжений рассмотрим три стороны задачи.
Статическая сторона задачи.
Составим возможные уравнения статического равновесия для отсеченной части (рисунок 7.1,б)
N = òsdA = 0 , |
M y = òsxdA = 0 , |
Mx = òsydA- М = 0, (7.1) |
A |
A |
A |
114

Геометрическая сторона задачи.
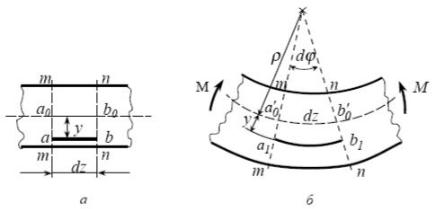
Вырежем из балки элемент длиной dz. После приложения нагрузки он выглядит следующим образом:
 в
в
Рисунок 7.2 - К выводу формулы нормальных напряжений при чистом изгибе
r - радиус нейтральной линии. dq - угол поворота сечения.
ab = dz – длина нейтральной линии для выбранного элемента.
Выделим волокно длиной a1b1 на расстоянии y от нейтральной линии. До де-
формации его длина равнялась ab. Относительное изменение длины волокна:
ea b = a1b1 - ab = |
(r + y)dq - rdq = |
y . |
||||
|
|
|
|
|
|
(7.2) |
|
ab |
rdq |
r |
|||
1 1
Это равенство является аналитическим выражением гипотезы плоских сечений.
Физическая сторона задачи.
Так как предполагается, что продольные волокна не давят друг на друга,
то согласно закону Гука нормальные напряжения в волокне ab равны
s = Ee |
(7.3) |
Подставим выражение 7.3 |
в формулу 7.2 |
s = y Е . (7.4) r
Отношение E/ρ в сечении есть величина постоянная, следовательно, на-
пряжения и зменяются по линейному закону(рисунок 7.2,в ). Для определе-
115
ния нормальных напряжений необходимо знать положение нейтрального слоя,
то есть ρ. Для этого рассмотрим условия равновесия (7.1)
При подстановка (7.4) в первое условие (7.1) имеем:
|
E |
|
E |
|
|
E |
(7.5) |
|
N = ò |
y × dA = |
ò y × dA = |
Sx = 0 . |
|||||
|
ρ |
ρ |
||||||
A ρ |
|
A |
|
|
||||
Так как E/ρ≠0, следовательно |
ò ydA = Sx = 0 |
|||||||
|
|
|
|
|
A |
|
||
Данный интеграл есть статический момент площади поперечного сечения относительно нейтральной линии x; он равен нулю, следовательно, нейтраль-
ная линия проходят через центр тяжести поперечного сечения, то есть
являются центральной осью.
При подстановке (7.4) во второе условие (7.1) имеем:
|
M y = ò |
|
E |
yx × dA = |
E |
|
ò yx × dA = |
E |
J xy = 0 , |
(7.6) |
||||||||
|
ρ |
ρ |
|
|
||||||||||||||
|
|
|
A |
|
|
A |
|
ρ |
|
|||||||||
откуда Jxy=0, т.е. ось x – главная. |
|
|
|
|
|
|||||||||||||
Таким образом, оси x,y являются главными центральными осями. |
||||||||||||||||||
При подстановке (7.4) в третье условие (7.1) получаем: |
|
|||||||||||||||||
|
M y = ò |
E |
yx×dA- М = |
E |
ò yx×dA- М = |
E |
Jxy - М = 0 , |
(7.7) |
||||||||||
|
|
ρ |
|
|
||||||||||||||
|
|
|
Aρ |
|
|
|
A |
|
|
ρ |
|
|||||||
Откуда радиус кривизны нейтрального слоя равен |
|
|||||||||||||||||
1 |
= |
M x |
|
. |
|
|
|
|
|
|
|
|
|
(7.8) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
r |
|
EJ x |
|
|
|
|
|
|
|
|
|
|
|||||
Произведение EJx называется жесткостью поперечного сечения при изги-
бе. Подставим (7.8) в уравнение (7.4)
s |
= Ey |
|
M x |
= |
M x y |
(7.9) |
|||
|
|
|
|
|
. |
||||
|
EJ x |
|
J x |
||||||
|
|
|
|
|
|
|
|||
Таким образом, абсолютная величина напряжения тем выше, чем больше |
|||||||||
расстояние y от нейтральной линии. Максимальное напряжение: |
|||||||||
s |
|
= |
M x ymax |
, |
(7.10) |
||||
max |
|
||||||||
|
|
||||||||
|
|
|
J x |
|
|
|
|
||
|
|
|
|
|
|
|
|
||
где ymax – расстояние от нейтральной линии до наиболее удаленной точки сече-
ния. Введем следующее обозначение:
116
|
J x |
= W - момент сопротивления, тогда условие прочности при чистом изгибе |
||
|
|
|||
|
|
x |
|
|
|
ymax |
|
|
|
можно записать следующим образом: |
||||
|
|
|
M x |
(7.11) |
|
|
σmax = |
|
£ [σ]. |
|
|
Wx |
||
|
|
|
|
|
При чистом изгибе по одну сторону от нейтрального слоя происходит простое растяжение, по другую – простое сжатие. Следовательно, при чистом изгибе имеет место линейное напряженное состояние:
-в растянутой зоне σ1>0, σ2=σ3=0;
-в сжатой зоне σ3>0, σ1=σ3=0.
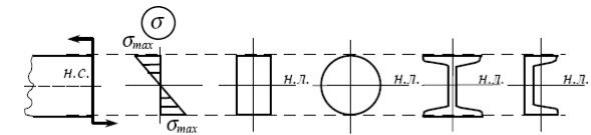
Эпюры нормальных напряжений (рисунок 7.2, в) показывают, что внут-
ренние слои материала нагружаются меньше, чем наружные. Поэтому, проек-
тируя профили балок, стремятся большую часть площади сечения разместить подальше от нейтральной линии. При изгибе в вертикальной плоскости стан-
дартные двутавровые, швеллерные, тавровые профили (рисунок 7.3) дают су-
щественную выгоду в весе.
Рисунок 7.3 - Распределение нормальных напряжений по высоте сечения при изгибе
Если материал балки хуже сопротивляется растяжению, нежели сжатию,
то центр тяжести сечения должен располагаться ближе к растянутым волокнам,
чтобы величина максимальных растягивающих напряжений была меньше мак-
симальных сжимающих напряжений.
117
